《2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版》

7.【题型一、三】(2025·黑龙江哈尔滨七十三中高一下月考)在海岸 $A$ 处发现北偏西 $75^{\circ}$ 的方向、与 $A$ 距离 $2$ 海里的 $B$ 处有一艘走私船，在 $A$ 处北偏东 $45^{\circ}$ 方向、与 $A$ 距离($\sqrt{3} - 1$)海里的 $C$ 处的缉私船奉命以 $10\sqrt{3}$ 海里/时的速度追截走私船.此时，走私船正以 $10$ 海里/时的速度从 $B$ 向北偏西 $30^{\circ}$ 方向逃窜.
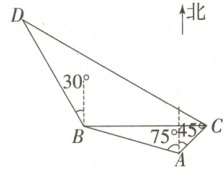
(1)刚发现走私船时，缉私船距离走私船多远？在走私船的什么方向？
(2)缉私船沿什么方向能最快追上走私船？

答案： 7.解:
(1)由题意,可得AB = 2,AC = $\sqrt{3}$ - 1,∠BAC = 120°,所以BC = $\sqrt{AB^2 + AC^2 - 2AB·AC·\cos\angle BAC}$ = $\sqrt{4 + 4 - 2\sqrt{3} + 2\sqrt{3} - 2}$ = $\sqrt{6}$,在△ABC中，由正弦定理得$\frac{AB}{\sin\angle ACB}$ = $\frac{BC}{\sin\angle BAC}$,即$\frac{2}{\sin\angle ACB}$ = $\frac{\sqrt{6}}{\frac{\sqrt{3}}{2}}$,解得sin∠ACB = $\frac{\sqrt{2}}{2}$,因为0° ＜ ∠ACB ＜ 180° - 120° = 60°,所以∠ACB = 45°,所以BC为水平线,所以刚发现走私船时,缉私船距离走私船$\sqrt{6}$海里，在走私船的正东方向.
(2)设经过t小时后，缉私船追上走私船，在△BCD中,可得BD = 10t,CD = 10$\sqrt{3}$t,∠DBC = 120°,由正弦定理得sin∠BCD = $\frac{BD\sin\angle CBD}{CD}$ = $\frac{10t×\frac{\sqrt{3}}{2}}{10\sqrt{3}t}$ = $\frac{1}{2}$,因为∠BCD为锐角，所以∠BCD = 30°,所以缉私船沿北偏西60°的方向能最快追上走私船.

8.【题型三】如图所示，某住宅小区一侧有一块三角形空地 $ABO$，其中 $OA = 3\ km$，$OB = 3\sqrt{3}\ km$，$\angle AOB = 90^{\circ}$.物业管理部门拟在中间开挖一个三角形人工湖 $OMN$，其中 $M$，$N$ 都在边 $AB$ 上($M$，$N$ 均不与 $A$，$B$ 重合，$M$ 在点 $A$，$N$ 之间)，且 $\angle MON = 30^{\circ}$.
(1)若 $M$ 在距离 $A$ 点 $1\ km$ 处，求点 $M$，$N$ 之间的距离.
(2)设 $\angle BON = \theta$.
①求 $\triangle OMN$ 的面积 $S$ 关于 $\theta$ 的表达式；
②为节省投入资金，三角形人工湖 $OMN$ 的面积要尽可能小，试确定 $\theta$ 的值，使 $\triangle OMN$ 的面积最小，并求出这个最小面积.

答案： 8.解:
(1)
∵AM = 1 km,OA = 3 km,OB = 3$\sqrt{3}$ km,∠AOB = 90°,
∴AB = 6 km,A = 60°,
∴OM = $\sqrt{9 + 1 - 2×3×1×\frac{1}{2}}$ = $\sqrt{7}$(km),cos∠AMO = $\frac{7 + 1 - 9}{2\sqrt{7}×1}$ = -$\frac{1}{2\sqrt{7}}$,sin∠AMO = $\frac{3\sqrt{3}}{2\sqrt{7}}$,
∴sin∠ONM = sin(∠AMO - ∠MON) = $\frac{3\sqrt{3}}{2\sqrt{7}}$·$\frac{\sqrt{3}}{2}$ + $\frac{1}{2\sqrt{7}}$·$\frac{1}{2}$ = $\frac{10}{4\sqrt{7}}$ = $\frac{5}{2\sqrt{7}}$,在△MON中,$\frac{MN}{\sin 30°}$ = $\frac{OM}{\sin\angle ONM}$ ⇒ MN = $\sqrt{7}$×$\frac{2\sqrt{7}}{5}$×$\frac{1}{2}$ = $\frac{7}{5}$.
(2)①
∵∠BON = θ,
∴∠ONM = θ + $\frac{\pi}{6}$,在△BON中，$\frac{ON}{\sin\frac{\pi}{6}}$ = $\frac{\frac{3\sqrt{3}}{2}}{\sin(\theta + \frac{\pi}{6})}$ ⇒ ON = $\frac{3\sqrt{3}}{2\sin(\theta + \frac{\pi}{6})}$(km),在△MON中，$\frac{MN}{\sin\frac{\pi}{6}}$ = $\frac{\frac{3\sqrt{3}}{2}}{\sin(\theta + \frac{\pi}{6})}$,
∴MN = $\frac{3\sqrt{3}}{2\sin(\theta + \frac{\pi}{6})}$(km),
∴S = $\frac{1}{2}$·$\frac{3\sqrt{3}}{2}$·$\frac{3\sqrt{3}}{2\sin(\theta + \frac{\pi}{6})}$ = $\frac{27}{4(\sqrt{3} + 2\sin2\theta)}$(km²),0 ＜ θ ＜ $\frac{\pi}{3}$.
②当sin2θ = 1,即θ = $\frac{\pi}{4}$时,S△OMN最小,且(S△OMN)min = $\frac{27}{4(\sqrt{3} + 2)}$ = $\frac{27(2 - \sqrt{3})}{4}$(km²).