2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
2.【题型二】(2025·黑龙江哈尔滨三中高一下月考) 如图所示,一条河两岸平行,河的宽度为 $400$ 米,一艘船从河岸的 $A$ 地出发,向河对岸航行. 已知船在静水中的航行速度 $\boldsymbol{v}_1$ 的大小为 $|\boldsymbol{v}_1| = 6\ km/h$,水流速度 $\boldsymbol{v}_2$ 的大小为 $|\boldsymbol{v}_2| = 2\ km/h$,船的速度与水流速度的合速度为 $\boldsymbol{v}$,那么当航程最短时,下列说法正确的是 (

A.船头方向与水流方向垂直
B.$\cos \langle \boldsymbol{v}_1, \boldsymbol{v}_2 \rangle = -\frac{1}{4}$
C.$|\boldsymbol{v}| = 4\sqrt{2}\ km/h$
D.该船到达对岸所需时间为 $3$ 分钟
C
)
A.船头方向与水流方向垂直
B.$\cos \langle \boldsymbol{v}_1, \boldsymbol{v}_2 \rangle = -\frac{1}{4}$
C.$|\boldsymbol{v}| = 4\sqrt{2}\ km/h$
D.该船到达对岸所需时间为 $3$ 分钟
答案:
2.C[提示:设$A'$是河对岸一点,且$AA'$与河岸垂直,那么当这艘船实际沿$AA'$方向行驶时船的航程最短,由$\boldsymbol{v} = \boldsymbol{v}_1 + \boldsymbol{v}_2$,得$|\boldsymbol{v}| = \sqrt{|\boldsymbol{v}_1|^2 - |\boldsymbol{v}_2|^2} = \sqrt{6^2 - 2^2} = 4\sqrt{2}\ ( km/h)$,故C正确;设船头方向与$AA'$的夹角为$\theta$,则$\sin\theta = \frac{|\boldsymbol{v}_2|}{|\boldsymbol{v}_1|} = \frac{2}{6} = \frac{1}{3}$,故船头方向与水流方向不垂直,故A错误;$\cos\langle\boldsymbol{v}_1,\boldsymbol{v}_2\rangle = \cos\left(\frac{\pi}{2} + \theta\right) = -\sin\theta = -\frac{1}{3}$,故B错误;该船到达对岸的时间为$\boldsymbol{t} = \frac{400}{4\sqrt{2}×1000} × 60 \approx 4.2\ ( 分钟)$,故D错误.

]
2.C[提示:设$A'$是河对岸一点,且$AA'$与河岸垂直,那么当这艘船实际沿$AA'$方向行驶时船的航程最短,由$\boldsymbol{v} = \boldsymbol{v}_1 + \boldsymbol{v}_2$,得$|\boldsymbol{v}| = \sqrt{|\boldsymbol{v}_1|^2 - |\boldsymbol{v}_2|^2} = \sqrt{6^2 - 2^2} = 4\sqrt{2}\ ( km/h)$,故C正确;设船头方向与$AA'$的夹角为$\theta$,则$\sin\theta = \frac{|\boldsymbol{v}_2|}{|\boldsymbol{v}_1|} = \frac{2}{6} = \frac{1}{3}$,故船头方向与水流方向不垂直,故A错误;$\cos\langle\boldsymbol{v}_1,\boldsymbol{v}_2\rangle = \cos\left(\frac{\pi}{2} + \theta\right) = -\sin\theta = -\frac{1}{3}$,故B错误;该船到达对岸的时间为$\boldsymbol{t} = \frac{400}{4\sqrt{2}×1000} × 60 \approx 4.2\ ( 分钟)$,故D错误.

]
3.【题型二】已知两个力 $\boldsymbol{F}_1, \boldsymbol{F}_2$ 的夹角为 $90°$,它们的合力大小为 $20\ N$,合力与 $\boldsymbol{F}_2$ 的夹角为 $60°$,那么 $\boldsymbol{F}_2$ 的大小为 (
A.$10\sqrt{3}\ N$
B.$10\ N$
C.$10\sqrt{2}\ N$
D.$20\ N$
B
)A.$10\sqrt{3}\ N$
B.$10\ N$
C.$10\sqrt{2}\ N$
D.$20\ N$
答案:
3.B[提示:设$\boldsymbol{F}_1$,$\boldsymbol{F}_2$的对应向量分别为$\overrightarrow{OA}$,$\overrightarrow{OB}$,以$OA$,$OB$为邻边作平行四边形$OACB$,如图所示,则$\overrightarrow{OC} = \overrightarrow{OA} + \overrightarrow{OB}$对应力$\boldsymbol{F}_1$,$\boldsymbol{F}_2$的合力.$\because \boldsymbol{F}_1$,$\boldsymbol{F}_2$的夹角为$90°$,$\therefore$四边形$OACB$是矩形,又合力与$\boldsymbol{F}_2$的夹角为$60°$,$\therefore$在$ Rt\triangle OCB$中,$\angle COB = 60°$,$|\overrightarrow{OC}| = 20\ N$,$\therefore |\overrightarrow{OB}| = |\overrightarrow{OC}|\cos60° = 20×\frac{1}{2} = 10\ ( N)$.

]
3.B[提示:设$\boldsymbol{F}_1$,$\boldsymbol{F}_2$的对应向量分别为$\overrightarrow{OA}$,$\overrightarrow{OB}$,以$OA$,$OB$为邻边作平行四边形$OACB$,如图所示,则$\overrightarrow{OC} = \overrightarrow{OA} + \overrightarrow{OB}$对应力$\boldsymbol{F}_1$,$\boldsymbol{F}_2$的合力.$\because \boldsymbol{F}_1$,$\boldsymbol{F}_2$的夹角为$90°$,$\therefore$四边形$OACB$是矩形,又合力与$\boldsymbol{F}_2$的夹角为$60°$,$\therefore$在$ Rt\triangle OCB$中,$\angle COB = 60°$,$|\overrightarrow{OC}| = 20\ N$,$\therefore |\overrightarrow{OB}| = |\overrightarrow{OC}|\cos60° = 20×\frac{1}{2} = 10\ ( N)$.

]
4.【题型一】(2025·黑龙江哈尔滨松雷中学高一下月考) 如图,在 $\triangle ABC$ 中,$D$ 为 $BC$ 的中点,$\overrightarrow{AE} = 2\overrightarrow{EC}$,$AD$ 与 $BE$ 交于点 $F$,若 $\overrightarrow{CF} = x\overrightarrow{AB} + y\overrightarrow{AC}$,则下面对于 $x, y$ 的描述正确的是 (
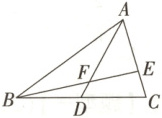
A.①③
B.②③
C.①④
D.②④
① $2x + 3y = -1$;
② $2x - 3y = 1$;
③ $x - y = 1$;
④ $x + y = -1$.
A
)
A.①③
B.②③
C.①④
D.②④
① $2x + 3y = -1$;
② $2x - 3y = 1$;
③ $x - y = 1$;
④ $x + y = -1$.
答案:
4.A[提示:因为$\overrightarrow{AE} = 2\overrightarrow{EC}$,所以$\overrightarrow{CA} = 3\overrightarrow{CE}$,结合题中等式可得$\overrightarrow{CF} = \boldsymbol{x}(\overrightarrow{CB} - \overrightarrow{CA}) - \boldsymbol{y}\overrightarrow{CA} = \boldsymbol{x}\overrightarrow{CB} - 3(\boldsymbol{x} + \boldsymbol{y})\overrightarrow{CE}$,由$F$,$B$,$E$三点共线,得$\boldsymbol{x} - 3(\boldsymbol{x} + \boldsymbol{y}) = 1$,即$2\boldsymbol{x} + 3\boldsymbol{y} = -1$,故①正确;因为$D$是$BC$的中点,所以$\overrightarrow{CB} = 2\overrightarrow{CD}$,可得$\overrightarrow{CF} = 2\boldsymbol{x}\overrightarrow{CD} - (\boldsymbol{x} + \boldsymbol{y})\overrightarrow{CA}$,根据$F$,$D$,$A$三点共线,可得$2\boldsymbol{x} - (\boldsymbol{x} + \boldsymbol{y}) = 1$,即$\boldsymbol{x} - \boldsymbol{y} = 1$,故③正确;根据①③正确,可知$\boldsymbol{x} = \frac{2}{5}$,$\boldsymbol{y} = -\frac{3}{5}$,故②④不正确.

]
4.A[提示:因为$\overrightarrow{AE} = 2\overrightarrow{EC}$,所以$\overrightarrow{CA} = 3\overrightarrow{CE}$,结合题中等式可得$\overrightarrow{CF} = \boldsymbol{x}(\overrightarrow{CB} - \overrightarrow{CA}) - \boldsymbol{y}\overrightarrow{CA} = \boldsymbol{x}\overrightarrow{CB} - 3(\boldsymbol{x} + \boldsymbol{y})\overrightarrow{CE}$,由$F$,$B$,$E$三点共线,得$\boldsymbol{x} - 3(\boldsymbol{x} + \boldsymbol{y}) = 1$,即$2\boldsymbol{x} + 3\boldsymbol{y} = -1$,故①正确;因为$D$是$BC$的中点,所以$\overrightarrow{CB} = 2\overrightarrow{CD}$,可得$\overrightarrow{CF} = 2\boldsymbol{x}\overrightarrow{CD} - (\boldsymbol{x} + \boldsymbol{y})\overrightarrow{CA}$,根据$F$,$D$,$A$三点共线,可得$2\boldsymbol{x} - (\boldsymbol{x} + \boldsymbol{y}) = 1$,即$\boldsymbol{x} - \boldsymbol{y} = 1$,故③正确;根据①③正确,可知$\boldsymbol{x} = \frac{2}{5}$,$\boldsymbol{y} = -\frac{3}{5}$,故②④不正确.

]
5.【题型一】设 $H$ 是 $\triangle ABC$ 的垂心,且 $3\overrightarrow{HA} +4\overrightarrow{HB} + 5\overrightarrow{HC} = 0$,则 $\cos \angle BHC$ 的值为 (
A.$-\frac{\sqrt{30}}{10}$
B.$-\frac{\sqrt{5}}{5}$
C.$-\frac{\sqrt{6}}{6}$
D.$-\frac{\sqrt{70}}{14}$
D
)A.$-\frac{\sqrt{30}}{10}$
B.$-\frac{\sqrt{5}}{5}$
C.$-\frac{\sqrt{6}}{6}$
D.$-\frac{\sqrt{70}}{14}$
答案:
5.D[提示:由三角形垂心性质得$\overrightarrow{HA}·\overrightarrow{HB} = \overrightarrow{HB}·\overrightarrow{HC} = \overrightarrow{HC}·\overrightarrow{HA}$,不妨设$\overrightarrow{HA}·\overrightarrow{HB} = \overrightarrow{HB}·\overrightarrow{HC} = \overrightarrow{HC}·\overrightarrow{HA} = \boldsymbol{x}$,$\because 3\overrightarrow{HA} + 4\overrightarrow{HB} + 5\overrightarrow{HC} = \boldsymbol{0}$,$\therefore 3\overrightarrow{HA}·\overrightarrow{HB} + 4\overrightarrow{HB}^2 + 5\overrightarrow{HC}·\overrightarrow{HB} = 0$,$\therefore |\overrightarrow{HB}| = \sqrt{-2\boldsymbol{x}}$,同理可求得$|\overrightarrow{HC}| = \sqrt{\frac{7\boldsymbol{x}}{5}}$,$\therefore \cos\angle BHC = \frac{\overrightarrow{HB}·\overrightarrow{HC}}{|\overrightarrow{HB}|·|\overrightarrow{HC}|} = \frac{\boldsymbol{x}}{\sqrt{-2\boldsymbol{x}}·\sqrt{\frac{7\boldsymbol{x}}{5}}} = \frac{\sqrt{70}}{14}$.]
6. (2025·黑龙江牡丹江市名校协作体高一下月考)
如图,在 $\triangle ABC$ 中,$D$ 是 $BC$ 的中点,$G$ 是 $AD$ 的中点,过点 $G$ 作直线分别交 $AB, AC$ 于点 $M,N$,且 $\overrightarrow{AB} = x\overrightarrow{AM}, \overrightarrow{AC} = y\overrightarrow{AN}$,则 $\frac{1}{x} + \frac{1}{y}$ 的最小值为 (

A.1
B.2
C.4
D.$\sqrt{2}$
如图,在 $\triangle ABC$ 中,$D$ 是 $BC$ 的中点,$G$ 是 $AD$ 的中点,过点 $G$ 作直线分别交 $AB, AC$ 于点 $M,N$,且 $\overrightarrow{AB} = x\overrightarrow{AM}, \overrightarrow{AC} = y\overrightarrow{AN}$,则 $\frac{1}{x} + \frac{1}{y}$ 的最小值为 (
A
)
A.1
B.2
C.4
D.$\sqrt{2}$
答案:
6.A[提示:因为$G$是$AD$的中点,且$\overrightarrow{AB} = \boldsymbol{x}\overrightarrow{AM}$,$\overrightarrow{AC} = \boldsymbol{y}\overrightarrow{AN}$,所以$\overrightarrow{AG} = \frac{1}{2}×\frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AC}) = \frac{1}{4}(\boldsymbol{x}\overrightarrow{AM} + \boldsymbol{y}\overrightarrow{AN})$.因为$M$,$G$,$N$三点共线,所以$\frac{1}{4}(\boldsymbol{x} + \boldsymbol{y}) = 1$,即$\boldsymbol{x} + \boldsymbol{y} = 4$,所以$\frac{1}{\boldsymbol{x}} + \frac{1}{\boldsymbol{y}} = \frac{1}{4}\left(\frac{1}{\boldsymbol{x}} + \frac{1}{\boldsymbol{y}}\right)(\boldsymbol{x} + \boldsymbol{y}) = \frac{1}{4}\left(2 + \frac{\boldsymbol{x}}{\boldsymbol{y}} + \frac{\boldsymbol{y}}{\boldsymbol{x}}\right) \geqslant \frac{1}{4}\left(2 + 2\sqrt{\frac{\boldsymbol{x}}{\boldsymbol{y}}·\frac{\boldsymbol{y}}{\boldsymbol{x}}}\right) = 1$,当且仅当$\boldsymbol{x} = \boldsymbol{y} = 2$时,等号成立.]
7.【题型一】(2025·黑龙江哈尔滨九中高一下月考) 已知正方形 $ABCD$ 的边长为 $3$,$\overrightarrow{DE} =\frac{1}{2}\overrightarrow{EC}$,若 $\overrightarrow{BE} = \lambda\overrightarrow{BA} + \mu\overrightarrow{BC}$,其中 $\lambda, \mu$ 为实数,则 $\lambda + \mu =$
$\frac{5}{3}$
;设 $F$ 是线段 $BE$ 上的动点,$G$ 为线段 $AF$ 的中点,则 $\overrightarrow{AF} · \overrightarrow{DG}$ 的最小值为-4
.
答案:
7.$\frac{5}{3}$,$-4$[提示:因为$\overrightarrow{DE} = \frac{1}{2}\overrightarrow{EC}$,所以$\overrightarrow{CE} = \frac{2}{3}\overrightarrow{CD}$,所以$\overrightarrow{BE} = \overrightarrow{BC} + \overrightarrow{CE} = \overrightarrow{BC} + \frac{2}{3}\overrightarrow{CD} = \overrightarrow{BC} + \frac{2}{3}\overrightarrow{BA}$,因为$\overrightarrow{BE} = \lambda\overrightarrow{BA} + \mu\overrightarrow{BC}$,所以由平面向量基本定理可得$\lambda = \frac{2}{3}$,$\mu = 1$,所以$\lambda + \mu = \frac{5}{3}$.因为$\overrightarrow{AF} = \overrightarrow{DF} - \overrightarrow{DA}$,$G$为线段$AF$的中点,所以$\overrightarrow{DG} = \frac{1}{2}(\overrightarrow{DA} + \overrightarrow{DF})$,又因为$|\overrightarrow{DA}| = 3$,所以$\overrightarrow{AF}·\overrightarrow{DG} = \frac{1}{2}(\overrightarrow{DF} - \overrightarrow{DA})(\overrightarrow{DA} + \overrightarrow{DF}) = \frac{1}{2}(\overrightarrow{DF}^2 - \overrightarrow{DA}^2) = \frac{1}{2}(|\overrightarrow{DF}|^2 - 9)$,因为$F$是线段$BE$上的动点,所以$|\overrightarrow{DE}| \leqslant |\overrightarrow{DF}| \leqslant |\overrightarrow{DB}|$,因为正方形$ABCD$的边长为$3$,且$\overrightarrow{DE} = \frac{1}{2}\overrightarrow{EC}$,所以$|\overrightarrow{DE}| = 1$,所以$\overrightarrow{AF}·\overrightarrow{DG} = \frac{1}{2}(|\overrightarrow{DF}|^2 - 9) \leqslant -4$,所以当点$F$与点$E$重合时,$\overrightarrow{AF}·\overrightarrow{DG}$取得最小值,最小值为$-4$.

]
7.$\frac{5}{3}$,$-4$[提示:因为$\overrightarrow{DE} = \frac{1}{2}\overrightarrow{EC}$,所以$\overrightarrow{CE} = \frac{2}{3}\overrightarrow{CD}$,所以$\overrightarrow{BE} = \overrightarrow{BC} + \overrightarrow{CE} = \overrightarrow{BC} + \frac{2}{3}\overrightarrow{CD} = \overrightarrow{BC} + \frac{2}{3}\overrightarrow{BA}$,因为$\overrightarrow{BE} = \lambda\overrightarrow{BA} + \mu\overrightarrow{BC}$,所以由平面向量基本定理可得$\lambda = \frac{2}{3}$,$\mu = 1$,所以$\lambda + \mu = \frac{5}{3}$.因为$\overrightarrow{AF} = \overrightarrow{DF} - \overrightarrow{DA}$,$G$为线段$AF$的中点,所以$\overrightarrow{DG} = \frac{1}{2}(\overrightarrow{DA} + \overrightarrow{DF})$,又因为$|\overrightarrow{DA}| = 3$,所以$\overrightarrow{AF}·\overrightarrow{DG} = \frac{1}{2}(\overrightarrow{DF} - \overrightarrow{DA})(\overrightarrow{DA} + \overrightarrow{DF}) = \frac{1}{2}(\overrightarrow{DF}^2 - \overrightarrow{DA}^2) = \frac{1}{2}(|\overrightarrow{DF}|^2 - 9)$,因为$F$是线段$BE$上的动点,所以$|\overrightarrow{DE}| \leqslant |\overrightarrow{DF}| \leqslant |\overrightarrow{DB}|$,因为正方形$ABCD$的边长为$3$,且$\overrightarrow{DE} = \frac{1}{2}\overrightarrow{EC}$,所以$|\overrightarrow{DE}| = 1$,所以$\overrightarrow{AF}·\overrightarrow{DG} = \frac{1}{2}(|\overrightarrow{DF}|^2 - 9) \leqslant -4$,所以当点$F$与点$E$重合时,$\overrightarrow{AF}·\overrightarrow{DG}$取得最小值,最小值为$-4$.

]
8.【题型一】在三角形 $ABC$ 中,设点 $M$ 是线段 $BC$ 的中点,且 $|\overrightarrow{BC}| = 4$,$|\overrightarrow{AB} + \overrightarrow{AC}| = |\overrightarrow{AB} - \overrightarrow{AC}|$,则 $|\overrightarrow{AM}| =$
2
.
答案:
8.2[提示:由$|\overrightarrow{AB} + \overrightarrow{AC}| = |\overrightarrow{AB} - \overrightarrow{AC}|$两边同时平方,得$\overrightarrow{AB}·\overrightarrow{AC} = 0$,即$\overrightarrow{AB} \perp \overrightarrow{AC}$,所以$\angle BAC = 90°$.在$ Rt\triangle ABC$中,因为点$M$是线段$BC$的中点,且$|\overrightarrow{BC}| = 4$,所以$|\overrightarrow{AM}| = \frac{1}{2}|\overrightarrow{BC}| = \frac{1}{2}×4 = 2$.]
9.【题型一】$\triangle ABC$ 的内角为 $A, B, C$,$A = \frac{\pi}{2}$,$AB = 1$,$AC = 2$,$BC$ 边上的高为 $AD$.
(1) 用 $\overrightarrow{AB}, \overrightarrow{AC}$ 表示 $\overrightarrow{AD}$;
(2) 若 $E$ 为 $AC$ 边上一点,且 $\overrightarrow{ED} · \overrightarrow{AD} = \frac{2}{5}$,试确定 $E$ 点的位置,并说明理由.
(1) 用 $\overrightarrow{AB}, \overrightarrow{AC}$ 表示 $\overrightarrow{AD}$;
(2) 若 $E$ 为 $AC$ 边上一点,且 $\overrightarrow{ED} · \overrightarrow{AD} = \frac{2}{5}$,试确定 $E$ 点的位置,并说明理由.
答案:
9.解:
(1)由题意得$BC = \sqrt{AB^2 + AC^2} = \sqrt{5}$.因为$\cos B = \frac{BD}{AB} = \frac{AB}{BC}$,所以$BD = \frac{AB^2}{BC} = \frac{\sqrt{5}}{5}$.又$BC = \sqrt{5}$,所以$\overrightarrow{BD} = \frac{1}{5}\overrightarrow{BC}$,所以$\overrightarrow{AD} = \overrightarrow{AB} + \overrightarrow{BD} = \overrightarrow{AB} + \frac{1}{5}\overrightarrow{BC} = \overrightarrow{AB} + \frac{1}{5}(\overrightarrow{AC} - \overrightarrow{AB}) = \frac{4}{5}\overrightarrow{AB} + \frac{1}{5}\overrightarrow{AC}$.
(2)设$\overrightarrow{AE} = \lambda\overrightarrow{AC}$.因为$\overrightarrow{ED} = \overrightarrow{EA} + \overrightarrow{AD} = -\lambda\overrightarrow{AC} + \frac{4}{5}\overrightarrow{AB} + \frac{1}{5}\overrightarrow{AC} = \frac{4}{5}\overrightarrow{AB} + \left(\frac{1}{5} - \lambda\right)\overrightarrow{AC}$,所以$\overrightarrow{ED}·\overrightarrow{AD} = \left[\frac{4}{5}\overrightarrow{AB} + \left(\frac{1}{5} - \lambda\right)\overrightarrow{AC}\right]·\left(\frac{4}{5}\overrightarrow{AB} + \frac{1}{5}\overrightarrow{AC}\right) = \frac{16}{25}\overrightarrow{AB}^2 + \frac{4}{25}\overrightarrow{AB}·\overrightarrow{AC} + \frac{4}{5}\left(\frac{1}{5} - \lambda\right)\overrightarrow{AB}·\overrightarrow{AC} + \frac{1}{5}\left(\frac{1}{5} - \lambda\right)\overrightarrow{AC}^2 = \frac{16}{25} + \frac{4}{5}\left(\frac{1}{5} - \lambda\right) = \frac{2}{5}$,解得$\lambda = \frac{1}{2}$,故$E$为$AC$的中点.
(1)由题意得$BC = \sqrt{AB^2 + AC^2} = \sqrt{5}$.因为$\cos B = \frac{BD}{AB} = \frac{AB}{BC}$,所以$BD = \frac{AB^2}{BC} = \frac{\sqrt{5}}{5}$.又$BC = \sqrt{5}$,所以$\overrightarrow{BD} = \frac{1}{5}\overrightarrow{BC}$,所以$\overrightarrow{AD} = \overrightarrow{AB} + \overrightarrow{BD} = \overrightarrow{AB} + \frac{1}{5}\overrightarrow{BC} = \overrightarrow{AB} + \frac{1}{5}(\overrightarrow{AC} - \overrightarrow{AB}) = \frac{4}{5}\overrightarrow{AB} + \frac{1}{5}\overrightarrow{AC}$.
(2)设$\overrightarrow{AE} = \lambda\overrightarrow{AC}$.因为$\overrightarrow{ED} = \overrightarrow{EA} + \overrightarrow{AD} = -\lambda\overrightarrow{AC} + \frac{4}{5}\overrightarrow{AB} + \frac{1}{5}\overrightarrow{AC} = \frac{4}{5}\overrightarrow{AB} + \left(\frac{1}{5} - \lambda\right)\overrightarrow{AC}$,所以$\overrightarrow{ED}·\overrightarrow{AD} = \left[\frac{4}{5}\overrightarrow{AB} + \left(\frac{1}{5} - \lambda\right)\overrightarrow{AC}\right]·\left(\frac{4}{5}\overrightarrow{AB} + \frac{1}{5}\overrightarrow{AC}\right) = \frac{16}{25}\overrightarrow{AB}^2 + \frac{4}{25}\overrightarrow{AB}·\overrightarrow{AC} + \frac{4}{5}\left(\frac{1}{5} - \lambda\right)\overrightarrow{AB}·\overrightarrow{AC} + \frac{1}{5}\left(\frac{1}{5} - \lambda\right)\overrightarrow{AC}^2 = \frac{16}{25} + \frac{4}{5}\left(\frac{1}{5} - \lambda\right) = \frac{2}{5}$,解得$\lambda = \frac{1}{2}$,故$E$为$AC$的中点.
1. 一物体受到 $3$ 个力的作用,其中重力 $\boldsymbol{G}$ 的大小为 $2\ N$,水平拉力 $\boldsymbol{F}_1$ 的大小为 $1\ N$,力 $\boldsymbol{F}_2$ 未知,则 (
A.当该物体处于平衡状态时,$|\boldsymbol{F}_2| = \sqrt{5}\ N$
B.当 $\boldsymbol{F}_2$ 与 $\boldsymbol{F}_1$ 方向相反,且 $|\boldsymbol{F}_2| = 5\ N$ 时,物体所受合力大小为 $0$
C.当 $|\boldsymbol{F}_2| = 1\ N$ 时,$(\sqrt{5} - 1)\ N \leqslant |\boldsymbol{F}_1 + \boldsymbol{F}_2 + \boldsymbol{G}| \leqslant (\sqrt{5} + 2)\ N$
D.当 $|\boldsymbol{F}_2| = 1\ N$ 时,必存在实数 $\lambda$,使得 $\boldsymbol{G} =\boldsymbol{F}_2 + \lambda\boldsymbol{F}_1$
AD
)A.当该物体处于平衡状态时,$|\boldsymbol{F}_2| = \sqrt{5}\ N$
B.当 $\boldsymbol{F}_2$ 与 $\boldsymbol{F}_1$ 方向相反,且 $|\boldsymbol{F}_2| = 5\ N$ 时,物体所受合力大小为 $0$
C.当 $|\boldsymbol{F}_2| = 1\ N$ 时,$(\sqrt{5} - 1)\ N \leqslant |\boldsymbol{F}_1 + \boldsymbol{F}_2 + \boldsymbol{G}| \leqslant (\sqrt{5} + 2)\ N$
D.当 $|\boldsymbol{F}_2| = 1\ N$ 时,必存在实数 $\lambda$,使得 $\boldsymbol{G} =\boldsymbol{F}_2 + \lambda\boldsymbol{F}_1$
答案:
1.AD[提示:对于A,当该物体处于平衡状态时,如图
(1)所示,此时$\boldsymbol{F}_1$,$\boldsymbol{F}_2$的合力大小为$2\ N$,方向与重力方向相反,故$|\boldsymbol{F}_2| = \sqrt{5}\ N$,正确;对于B,当$\boldsymbol{F}_2$与$\boldsymbol{F}_1$方向相反时,且$|\boldsymbol{F}_2| = 5\ N$时,物体所受合力大小为$\sqrt{(5 - 1)^2 + 2^2} = 2\sqrt{5}\ ( N)$,错误;对于C,当$|\boldsymbol{F}_2| = 1\ N$时,设重力$G$与水平拉力$\boldsymbol{F}_1$的合力为$\boldsymbol{F}$,$|\boldsymbol{F}| = \sqrt{5}\ N$,如图
(2)所示,当$\boldsymbol{F}_2$与$\boldsymbol{F}$方向相同时,$|\boldsymbol{F}_1 + \boldsymbol{F}_2 + G|$取得最大值$(\sqrt{5} + 1)\ N$,当$\boldsymbol{F}_2$与$\boldsymbol{F}$方向相反时,$|\boldsymbol{F}_1 + \boldsymbol{F}_2 + G|$取得最小值$(\sqrt{5} - 1)\ N$,故$(\sqrt{5} - 1)\ N \leqslant |\boldsymbol{F}_1 + \boldsymbol{F}_2 + G| \leqslant (\sqrt{5} + 1)\ N$,错误;对于D,当$|\boldsymbol{F}_2| = 1\ N$时,若存在实数$\lambda$,使得$G = \boldsymbol{F}_2 + \lambda\boldsymbol{F}_1$,则$\lambda^2 = (G - \boldsymbol{F}_2)^2 = 4 + 1 - 2×2×1\cos\theta = 5 - 4\cos\theta \in [1,9]$,其中$\theta$为力$G$,$\boldsymbol{F}_2$的夹角,所以存在实数$\lambda$,使得$G = \boldsymbol{F}_2 + \lambda\boldsymbol{F}_1$,故D正确.


]
1.AD[提示:对于A,当该物体处于平衡状态时,如图
(1)所示,此时$\boldsymbol{F}_1$,$\boldsymbol{F}_2$的合力大小为$2\ N$,方向与重力方向相反,故$|\boldsymbol{F}_2| = \sqrt{5}\ N$,正确;对于B,当$\boldsymbol{F}_2$与$\boldsymbol{F}_1$方向相反时,且$|\boldsymbol{F}_2| = 5\ N$时,物体所受合力大小为$\sqrt{(5 - 1)^2 + 2^2} = 2\sqrt{5}\ ( N)$,错误;对于C,当$|\boldsymbol{F}_2| = 1\ N$时,设重力$G$与水平拉力$\boldsymbol{F}_1$的合力为$\boldsymbol{F}$,$|\boldsymbol{F}| = \sqrt{5}\ N$,如图
(2)所示,当$\boldsymbol{F}_2$与$\boldsymbol{F}$方向相同时,$|\boldsymbol{F}_1 + \boldsymbol{F}_2 + G|$取得最大值$(\sqrt{5} + 1)\ N$,当$\boldsymbol{F}_2$与$\boldsymbol{F}$方向相反时,$|\boldsymbol{F}_1 + \boldsymbol{F}_2 + G|$取得最小值$(\sqrt{5} - 1)\ N$,故$(\sqrt{5} - 1)\ N \leqslant |\boldsymbol{F}_1 + \boldsymbol{F}_2 + G| \leqslant (\sqrt{5} + 1)\ N$,错误;对于D,当$|\boldsymbol{F}_2| = 1\ N$时,若存在实数$\lambda$,使得$G = \boldsymbol{F}_2 + \lambda\boldsymbol{F}_1$,则$\lambda^2 = (G - \boldsymbol{F}_2)^2 = 4 + 1 - 2×2×1\cos\theta = 5 - 4\cos\theta \in [1,9]$,其中$\theta$为力$G$,$\boldsymbol{F}_2$的夹角,所以存在实数$\lambda$,使得$G = \boldsymbol{F}_2 + \lambda\boldsymbol{F}_1$,故D正确.


]
2. 一个重 $20\ N$ 的物体从倾斜角为 $30°$、斜面长 $1\ m$ 的光滑斜面顶端下滑到底端,则重力做的功是
10
$J$.
答案:
2.10[提示:物体在重力方向上的位移为$1×\sin30° = \frac{1}{2}\ ( m)$,$\therefore$重力所做功$W = 20×\frac{1}{2} = 10\ ( J)$.]
查看更多完整答案,请扫码查看


