2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. (教材改编题)在$\triangle ABC$中,已知$AB=BC=3,AC=2$,则$\cos B$等于 (
A.$\frac{7}{9}$
B.$\frac{8}{9}$
C.$-\frac{7}{9}$
D.$-\frac{8}{9}$
A
)A.$\frac{7}{9}$
B.$\frac{8}{9}$
C.$-\frac{7}{9}$
D.$-\frac{8}{9}$
答案:
1.A[提示:在$\triangle ABC$中,因为$AB=BC=3$,$AC=2$,所以由余弦定理可得$\cos B=\frac{BC^{2}+AB^{2}-AC^{2}}{2BC· AB}=\frac{9+9-4}{2×3×3}=\frac{7}{9}$.]
2. (教材改编题)已知$A,B$两地相距$5 km$,$B,C$两地相距$10 km$,若测得$\angle ABC = 120°$,则$A,C$两地间的距离为(
A.$5 km$
B.$\frac{\sqrt{3}}{2} km$
C.$5\sqrt{5} km$
D.$5\sqrt{7} km$
D
)A.$5 km$
B.$\frac{\sqrt{3}}{2} km$
C.$5\sqrt{5} km$
D.$5\sqrt{7} km$
答案:
2.D[提示:在$\triangle ABC$中,由已知可得$AB=5$,$BC=10$,所以$AC^{2}=AB^{2}+BC^{2}-2AB· BC·\cos\angle ABC$,即$AC^{2}=5^{2}+10^{2}-2×5×10×(-\frac{1}{2})=175$,解得$AC=5\sqrt{7}$.故$A$,$C$两地间的距离为$5\sqrt{7}$km.]
3. 在$\triangle ABC$中,若$C = 60°$,$c^2 = ab$,则$\triangle ABC$的形状是 (
A.等腰直角三角形
B.直角三角形
C.等腰三角形
D.等边三角形
D
)A.等腰直角三角形
B.直角三角形
C.等腰三角形
D.等边三角形
答案:
3.D[提示:$\because C = 60^{\circ}$,$\therefore c^{2}=a^{2}+b^{2}-2ab\cos60^{\circ}=a^{2}+b^{2}-ab$,又$\because c^{2}=ab$,$\therefore a^{2}+b^{2}-ab=ab$,即$a^{2}+b^{2}-2ab=0$,整理得$(a - b)^{2}=0$,$\therefore a = b$,再结合$C = 60^{\circ}$得$\triangle ABC$是等边三角形.]
4. (教材改编题)已知钝角三角形$ABC$的内角$A,B,C$所对的边分别为$a,b,c$,且$a = k$,$b = k + 2$,$c = k + 4$,则$k$的取值范围是 (
A.$[1,5]$
B.$(2,5)$
C.$(2,6)$
D.$(1,6)$
C
)A.$[1,5]$
B.$(2,5)$
C.$(2,6)$
D.$(1,6)$
答案:
4.C[提示:由题意得$c$是最大边,即$C$是钝角,$\therefore$由余弦定理得$(k + 4)^{2}=(k + 2)^{2}+k^{2}-2k(k + 2)·\cos C>(k + 2)^{2}+k^{2}$,即$(k + 2)^{2}+k^{2}<(k + 4)^{2}$,解得$-2<k<6$,$\because a + b>c$,$\therefore k+(k + 2)>k + 4$,解得$k>2$.综上所述,$k$的取值范围是$(2,6)$.]
1.【题型二】(2025·黑龙江哈尔滨七十三中高一下月考)在$\triangle ABC$中,$a = 7$,$b = 10$,$c = 6$,则$\triangle ABC$是 (
A.钝角三角形
B.直角三角形
C.锐角三角形
D.等边三角形
A
)A.钝角三角形
B.直角三角形
C.锐角三角形
D.等边三角形
答案:
1.A[提示:在$\triangle ABC$中,因为$a = 7$,$b = 10$,$c = 6$,所以$b>a>c$,所以$B>A>C$,由余弦定理可知$\cos B=\frac{a^{2}+c^{2}-b^{2}}{2ac}=\frac{49 + 36-100}{2×7×6}=-\frac{5}{28}<0$,所以角$B$为钝角,故$\triangle ABC$为钝角三角形.]
2.【题型一】(2025·吉林长春市实验中学高一下第一学程考试)已知在$\triangle ABC$中,$AB = 5$,$BC = 4$,$\cos B = \frac{4}{5}$,则$BC$边上的中线长为 (
A.$\sqrt{17}$
B.$\sqrt{13}$
C.$\sqrt{45}$
D.$\sqrt{21}$
B
)A.$\sqrt{17}$
B.$\sqrt{13}$
C.$\sqrt{45}$
D.$\sqrt{21}$
答案:
2.B[提示:设$BC$的中点为$D$,则$\triangle ABD$中,$AB = 5$,$BD=\frac{1}{2}BC = 2$,$\cos B=\frac{4}{5}$,所以由余弦定理得$AD=\sqrt{AB^{2}+BD^{2}-2AB· BD\cos B}=\sqrt{25 + 4-2×5×2×\frac{4}{5}}=\sqrt{13}$.]
3.【题型一】已知$\triangle ABC$中角$A,B,C$所对的边分别为$a,b,c$,且$b\cos C = (2a - c)\cos B$,$ac = 3$,$b = 3$,则$a + c$等于 (
A.$4$
B.$6$
C.$2\sqrt{5}$
D.$3\sqrt{2}$
D
)A.$4$
B.$6$
C.$2\sqrt{5}$
D.$3\sqrt{2}$
答案:
3.D[提示:$\because b\cos C=(2a - c)\cos B$,由余弦定理可得$b·\frac{a^{2}+b^{2}-c^{2}}{2ab}=(2a - c)·\frac{a^{2}+c^{2}-b^{2}}{2ac}$,整理得$ac=a^{2}+c^{2}-b^{2}$,$\therefore\frac{a^{2}+c^{2}-b^{2}}{2ac}=\frac{1}{2}$,即$\cos B=\frac{1}{2}$,而$B\in(0,\pi)$,$\therefore B=\frac{\pi}{3}$.又$ac = 3$,$b = 3$,$\therefore$由余弦定理可得$9=a^{2}+c^{2}-ac=(a + c)^{2}-3ac=(a + c)^{2}-9$,$\therefore(a + c)^{2}=18$,$\therefore a + c = 3\sqrt{2}$.]
4.【题型一】(2025·黑龙江哈尔滨师大附中高一下月考)在$\triangle ABC$中,角$A,B,C$所对的边分别为$a,b,c$,$a^2 + b^2 - c^2 = 2\sqrt{3}ab\sin C$,且$|\overrightarrow{AB} + \overrightarrow{AC}| = |\overrightarrow{BC}|$,则$B$等于 (
A.$\frac{\pi}{2}$
B.$\frac{\pi}{4}$
C.$\frac{\pi}{3}$
D.$\frac{\pi}{6}$
C
)A.$\frac{\pi}{2}$
B.$\frac{\pi}{4}$
C.$\frac{\pi}{3}$
D.$\frac{\pi}{6}$
答案:
4.C[提示:由余弦定理结合$a^{2}+b^{2}-c^{2}=2\sqrt{3}ab\sin C$,可得$a^{2}+b^{2}-c^{2}=2ab\cos C=2\sqrt{3}ab\sin C$,$\therefore\tan C=\frac{\sqrt{3}}{3}$,又$C\in(0,\pi)$,$\therefore C=\frac{\pi}{6}$,由$|\overrightarrow{AB}+\overrightarrow{AC}|=|\overrightarrow{BC}|=|\overrightarrow{AC}-\overrightarrow{AB}|$,两边平方可得$\overrightarrow{AB}·\overrightarrow{AC}=0$,$\therefore A=\frac{\pi}{2}$,$\therefore B=\frac{\pi}{3}$.]
5.【题型一】(2025·黑龙江哈尔滨师大附中高一下期中)在$\triangle ABC$中,$a = 3$,$b = 4$,$A = \frac{\pi}{4}$,则$c =$
$2\sqrt{2}+1$
或$2\sqrt{2}-1$
.
答案:
5.$2\sqrt{2}+1$ $2\sqrt{2}-1$[提示:根据题意可知$a = 3$,$b = 4$,$A=\frac{\pi}{4}$,根据余弦定理得$a^{2}=b^{2}+c^{2}-2bc\cos A$,即$9 = 16+c^{2}-4\sqrt{2}c$,解得$c = 2\sqrt{2}+1$或$c = 2\sqrt{2}-1$,经检验,符合题意,所以$c = 2\sqrt{2}+1$或$c = 2\sqrt{2}-1$.]
6.【题型一】$\triangle ABC$的内角$A,B,C$的对边分别为$a,b,c$.若$\triangle ABC$的面积为$\frac{a^2 + b^2 - c^2}{4}$,则$C =$
$45^{\circ}$
.
答案:
6.$45^{\circ}$[提示:由余弦定理可知$\cos C=\frac{a^{2}+b^{2}-c^{2}}{2ab}$,$\therefore a^{2}+b^{2}-c^{2}=2ab\cos C$.$\because S=\frac{1}{2}ab\sin C=\frac{1}{4}(a^{2}+b^{2}-c^{2})=\frac{1}{2}ab\cos C$,$\therefore\sin C=\cos C$.$\because0<C<\pi$,$\therefore C = 45^{\circ}$.]
7.【题型一】在$\triangle ABC$中,角$A,B,C$所对的边分别为$a,b,c$,且满足$a^2 + b^2 + c^2 = 2\sqrt{3}ab\sin C$.若$A,B,C,D$四点共圆,且点$D$与点$A$位于直线$BC$的两侧,$AB = 3$,$BD = \sqrt{3}$,则$AD =$
$2\sqrt{3}$
.
答案:
7.$2\sqrt{3}$[提示:由余弦定理可得$a^{2}+b^{2}-c^{2}=2ab\cos C$,又$a^{2}+b^{2}+c^{2}=2\sqrt{3}ab\sin C$,把此等式与余弦定理中的等式相加得$a^{2}+b^{2}=ab(\sqrt{3}\sin C+\cos C)=2ab\sin(C+\frac{\pi}{6})$,再由不等式$a^{2}+b^{2}\geq2ab$,当且仅当$a = b$时,等号成立,得不等式可以化简为$\sin(C+\frac{\pi}{6})\geq1$.$\because\sin(C+\frac{\pi}{6})\leq1$,$\therefore\sin(C+\frac{\pi}{6}) = 1$,解得$C=\frac{\pi}{3}$,故三角形$ABC$为正三角形.又$\because A$,$B$,$C$,$D$四点共圆,$\therefore\angle BDC=\frac{2\pi}{3}$.在$\triangle BCD$中,根据余弦定理可知$\cos\angle BDC=\frac{BD^{2}+CD^{2}-BC^{2}}{2BD· CD}=-\frac{1}{2}$,解得$CD=\sqrt{3}$($CD=- \sqrt{3}$舍去),$\because BD = CD=\sqrt{3}$,$\angle BDC=\frac{2\pi}{3}$,$\therefore\angle CBD=\angle BCD=\frac{\pi}{6}$,$\therefore\angle ABD=\angle ABC+\angle CBD=\frac{\pi}{2}$,$\therefore AD=\sqrt{AB^{2}+BD^{2}}=2\sqrt{3}$.]
8.【题型一】在$\triangle ABC$中,$D$是$BC$边上一点,且$B = \frac{\pi}{6}$,$\frac{AD}{BD} = \frac{1}{2}$,若$D$是$BC$的中点,则$\frac{AC}{AB} =$
$\frac{\sqrt{21}}{3}$
;若$AC = 4\sqrt{3}$,则$\triangle ADC$的周长的最大值为$8 + 4\sqrt{3}$
.
答案:
8.$\frac{\sqrt{21}}{3}$ $8 + 4\sqrt{3}$[提示:如图所示,若$D$为$BC$的中点,则

$\frac{BD}{AD}=\frac{BD}{\frac{1}{2}BC}=\frac{1}{2}$,$B=\frac{\pi}{6}$,在$\triangle ABD$中,由余弦定理可得$AD^{2}=BD^{2}+AB^{2}-2AB· BD·\cos B$,即$\frac{BD^{2}}{4}=BD^{2}+AB^{2}-2AB· BD·\frac{\sqrt{3}}{2}$,所以$AC^{2}=4BD^{2}+\frac{3}{4}BD^{2}-\sqrt{3}·2×\frac{\sqrt{3}}{2}BD^{2}=\frac{7}{4}BD^{2}$,所以$\frac{AC}{AB}=\frac{\frac{\sqrt{7}}{2}BD}{\frac{\sqrt{3}}{2}BD}=\frac{\sqrt{21}}{3}$.若$AC = 4\sqrt{3}$,$B=\frac{\pi}{6}$,$BD = 2AD$,由上述可知$AB=\frac{\sqrt{3}}{2}BD=\frac{\sqrt{3}}{2}·2AD$,作$DE\perp AB$于点$E$,因为$B=\frac{\pi}{6}$,$\frac{BD}{2}=AD$,即点$E$与$A$重合,所以$DA\perp AB$,$\angle ADB=\frac{\pi}{3}$,所以$\angle ADC=\frac{2\pi}{3}$,在$\triangle ADC$中,由余弦定理得$\cos\angle ADC=\frac{AD^{2}+CD^{2}-AC^{2}}{2AD· CD}$,所以$-\frac{1}{2}=\frac{AD^{2}+CD^{2}-48}{2AD· CD}$,即$AD^{2}+CD^{2}=48 - AD· CD$,所以$(AD + CD)^{2}=48 + AD· CD$.又因为$AD· CD\leq\frac{(AD + CD)^{2}}{4}$,所以$(AD + CD)^{2}-48\leq\frac{(AD + CD)^{2}}{4}$,解得$AD + CD\leq8$,当且仅当$AD = CD = 4$时,等号成立,所以$AD + CD + AC\leq8 + 4\sqrt{3}$,即$\triangle ADC$的周长的最大值为$8 + 4\sqrt{3}$.]
8.$\frac{\sqrt{21}}{3}$ $8 + 4\sqrt{3}$[提示:如图所示,若$D$为$BC$的中点,则

$\frac{BD}{AD}=\frac{BD}{\frac{1}{2}BC}=\frac{1}{2}$,$B=\frac{\pi}{6}$,在$\triangle ABD$中,由余弦定理可得$AD^{2}=BD^{2}+AB^{2}-2AB· BD·\cos B$,即$\frac{BD^{2}}{4}=BD^{2}+AB^{2}-2AB· BD·\frac{\sqrt{3}}{2}$,所以$AC^{2}=4BD^{2}+\frac{3}{4}BD^{2}-\sqrt{3}·2×\frac{\sqrt{3}}{2}BD^{2}=\frac{7}{4}BD^{2}$,所以$\frac{AC}{AB}=\frac{\frac{\sqrt{7}}{2}BD}{\frac{\sqrt{3}}{2}BD}=\frac{\sqrt{21}}{3}$.若$AC = 4\sqrt{3}$,$B=\frac{\pi}{6}$,$BD = 2AD$,由上述可知$AB=\frac{\sqrt{3}}{2}BD=\frac{\sqrt{3}}{2}·2AD$,作$DE\perp AB$于点$E$,因为$B=\frac{\pi}{6}$,$\frac{BD}{2}=AD$,即点$E$与$A$重合,所以$DA\perp AB$,$\angle ADB=\frac{\pi}{3}$,所以$\angle ADC=\frac{2\pi}{3}$,在$\triangle ADC$中,由余弦定理得$\cos\angle ADC=\frac{AD^{2}+CD^{2}-AC^{2}}{2AD· CD}$,所以$-\frac{1}{2}=\frac{AD^{2}+CD^{2}-48}{2AD· CD}$,即$AD^{2}+CD^{2}=48 - AD· CD$,所以$(AD + CD)^{2}=48 + AD· CD$.又因为$AD· CD\leq\frac{(AD + CD)^{2}}{4}$,所以$(AD + CD)^{2}-48\leq\frac{(AD + CD)^{2}}{4}$,解得$AD + CD\leq8$,当且仅当$AD = CD = 4$时,等号成立,所以$AD + CD + AC\leq8 + 4\sqrt{3}$,即$\triangle ADC$的周长的最大值为$8 + 4\sqrt{3}$.]
9.【题型一】如图所示,一座山高$AD$为$100 m$,一辆汽车在一条水平的公路上沿直线从$B$往$C$匀速行驶,在$B$处测得山顶$A$的仰角为$30°$,经过$20 s$后汽车到达$C$处,这时测得山顶$A$的仰角为$45°$,且$\angle BAC = 90°$.
(1)求这辆汽车的速度;
(2)若汽车从$B$往$C$行驶$5 s$时到达$E$处,求此时山顶$A$与汽车的距离$AE$.
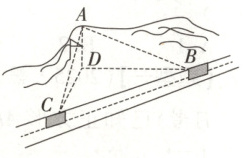
(1)求这辆汽车的速度;
(2)若汽车从$B$往$C$行驶$5 s$时到达$E$处,求此时山顶$A$与汽车的距离$AE$.

答案:
9.解:
(1)根据题意得$AD = 100 m$,$\angle DBA = 30^{\circ}$,$\angle ACD = 45^{\circ}$,$\triangle ACD$和$\triangle ABD$都是直角三角形,所以$AC = \sqrt{2}AD = 100\sqrt{2} m$,$AB = 200 m$,$BD = 100\sqrt{3} m$,由于$\angle BAC = 90^{\circ}$,所以$\triangle ABC$为直角三角形,所以$BC=\sqrt{(100\sqrt{2})^{2}+200^{2}}=100\sqrt{6}( m)$,所以这辆汽车的速度$v=\frac{100\sqrt{6}}{20}=5\sqrt{6}( m/s)$.
(2)汽车从$B$往$C$行驶$5 s$时到达$E$处,故$BE = 25\sqrt{6} m$,在$ Rt\triangle ABC$中,$\cos\angle ABC=\frac{200}{100\sqrt{6}}=\frac{\sqrt{6}}{3}$,在$\triangle ABE$中,利用余弦定理得$AE^{2}=AB^{2}+BE^{2}-2· AB· BE·\cos\angle ABC=200^{2}+(25\sqrt{6})^{2}-2×200×25\sqrt{6}×\frac{\sqrt{6}}{3}=23750$,解得$AE = 25\sqrt{38}( m)$.
(1)根据题意得$AD = 100 m$,$\angle DBA = 30^{\circ}$,$\angle ACD = 45^{\circ}$,$\triangle ACD$和$\triangle ABD$都是直角三角形,所以$AC = \sqrt{2}AD = 100\sqrt{2} m$,$AB = 200 m$,$BD = 100\sqrt{3} m$,由于$\angle BAC = 90^{\circ}$,所以$\triangle ABC$为直角三角形,所以$BC=\sqrt{(100\sqrt{2})^{2}+200^{2}}=100\sqrt{6}( m)$,所以这辆汽车的速度$v=\frac{100\sqrt{6}}{20}=5\sqrt{6}( m/s)$.
(2)汽车从$B$往$C$行驶$5 s$时到达$E$处,故$BE = 25\sqrt{6} m$,在$ Rt\triangle ABC$中,$\cos\angle ABC=\frac{200}{100\sqrt{6}}=\frac{\sqrt{6}}{3}$,在$\triangle ABE$中,利用余弦定理得$AE^{2}=AB^{2}+BE^{2}-2· AB· BE·\cos\angle ABC=200^{2}+(25\sqrt{6})^{2}-2×200×25\sqrt{6}×\frac{\sqrt{6}}{3}=23750$,解得$AE = 25\sqrt{38}( m)$.
查看更多完整答案,请扫码查看


