2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
2.【题型二】(2025·浙江杭州高级中学高三上月考)如图,在平行六面体$ABCD - A_1B_1C_1D_1$中,$E$是$AB$的中点,过$B_1$,$D_1$,$E$三点的截面$D_1B_1EF$把平行六面体分成两个部分,则左右两部分体积之比为
(

A.$3:4$
B.$5:7$
C.$4:7$
D.$7:17$
(
D
)
A.$3:4$
B.$5:7$
C.$4:7$
D.$7:17$
答案:
2.D[提示:因为平面ABCD//平面$A_{1}B_{1}C_{1}D_{1},$且截面$D_{1}B_{1}EF∩$平面ABCD = EF,截面$D_{1}B_{1}EF∩$平面$A_{1}B_{1}C_{1}D_{1}=B_{1}D_{1},$设平行六面体的底面面积为2S,高为h,由棱台体积公式,得$V_{左}=\frac{1}{3}(S+\frac{S}{4}+\sqrt{S·\frac{S}{4}})· h=\frac{7}{12}Sh,$所以$V_{右}=2Sh - \frac{7}{12}Sh,$所以$V_{左}:V_{右}=7:17.]$
3.【题型一】(2025·黑龙江哈尔滨三十二中高一下期中)如图,在正方体$ABCD - A_1B_1C_1D_1$的八个顶点中,有四个顶点$A$,$B_1$,$C$,$D_1$恰好是正四面体的顶点,则此正四面体的表面积与正方体的表面积之比为
(

A.$\sqrt{3}:1$
B.$1:\sqrt{2}$
C.$\sqrt{6}:2$
D.$1:\sqrt{3}$
(
D
)
A.$\sqrt{3}:1$
B.$1:\sqrt{2}$
C.$\sqrt{6}:2$
D.$1:\sqrt{3}$
答案:
3.D[提示:设正方体的棱长为a,则正方体的表面积是$6a^{2},$正四面体$A - B_{1}CD_{1}$的棱长为$\sqrt{2}a,$它的表面积是$4×\frac{1}{2}×(\sqrt{2}a)^{2}×\sin\frac{\pi}{3}=2\sqrt{3}a^{2},$所以正四面体的表面积与正方体的表面积之比为$2\sqrt{3}a^{2}:6a^{2}=1:\sqrt{3}.]$
4.【题型一、二】如图,若正四棱锥$P - ABCD$的底面边长为2,斜高为$\sqrt{5}$,则该正四棱锥的体积为
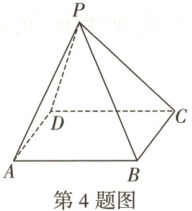
$\frac{8}{3}$
,表面积是$4+4\sqrt{5}$
.
答案:
$4.\frac{8}{3}+4\sqrt{5}[$提示:设该正四棱锥的高为h,
∵正四棱锥的底面边长为2,斜高为$\sqrt{5},$
∴$h=\sqrt{(\sqrt{5})^{2}-1^{2}}=2,$
∴体积$V=\frac{1}{3}×2^{2}×2=\frac{8}{3},$表面积$S=2×2 + 2×\sqrt{5}×\frac{1}{2}×4 = 4 + 4\sqrt{5}.]$
∵正四棱锥的底面边长为2,斜高为$\sqrt{5},$
∴$h=\sqrt{(\sqrt{5})^{2}-1^{2}}=2,$
∴体积$V=\frac{1}{3}×2^{2}×2=\frac{8}{3},$表面积$S=2×2 + 2×\sqrt{5}×\frac{1}{2}×4 = 4 + 4\sqrt{5}.]$
5.【题型二】(2025·黑龙江哈尔滨三中高一下期中)已知正三棱台$ABC - A_1B_1C_1$的体积是$21\sqrt{3}$,$AC = 6$,$A_1C_1 = 3$,则这个三棱台的高是
4
答案:
5.4[提示:根据题意可得上下底面正三角形的面积分别为$\frac{1}{2}×6×6×\frac{\sqrt{3}}{2}=9\sqrt{3},$$\frac{1}{2}×3×3×\frac{\sqrt{3}}{2}=\frac{9\sqrt{3}}{4},$设这个三棱台的高为h,所以这个三棱台的体积为$\frac{1}{3}×(9\sqrt{3}+\frac{9\sqrt{3}}{4}+\frac{9\sqrt{3}}{2})× h = 21\sqrt{3},$解得h = 4.]
6.【题型二】如图,已知三棱锥$A - BCD$中,$AB = AC = DB = DC = 3$,$AD = BC = 2$,$E$,$F$分别是$BD$,$CD$的中点,$P$是棱$AC$上(除端点外)的动点,则$PD + PB$的最小值为
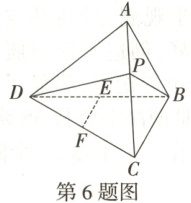
$\sqrt{17}$
;当$AP = 2PC$时,三棱锥$P - ABD$的体积为$\frac{4\sqrt{7}}{9}$
.
答案:
$6.\sqrt{17} \frac{4\sqrt{7}}{9}[$提示:因为AB = AC =DB = DC = 3,AD = BC = 2,所以将三棱锥的部分侧面展开铺平可得平行四边形ABCD,如图1,
在△ADC中,AD = 2,AC = DC = 3,由余弦定理可得$\cos\angle ADC=\frac{1}{3},$|$\overrightarrow{DB}$|=|$\overrightarrow{DA}+\overrightarrow{DC}$|$=\sqrt{\overrightarrow{DA}^{2}+\overrightarrow{DC}^{2}+2\overrightarrow{DA}·\overrightarrow{DC}}=\sqrt{17},$而$PD + PB≥DB=\sqrt{17},$所以PD + PB的最小值为$\sqrt{17}.$当AP = 2PC时,易知$V_{P - ABD}=\frac{2}{3}V_{C - ABD}.$因为AB = AC = DB = DC = 3,AD = BC = 2,所以可以构造如图2所示的长方体.设长方体的长、宽、高分别为a,b,c,则$\begin{cases}a^{2}+c^{2}=DB^{2}=9\\a^{2}+b^{2}=DC^{2}=9\end{cases},$解得$\begin{cases}a=\sqrt{7}\\b=c=\sqrt{2}\end{cases},$
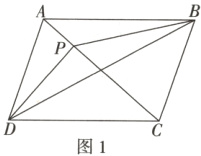
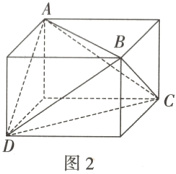
所以长方体的长为$\sqrt{7},$宽和高均为$\sqrt{2},$观察图形可知,三棱锥C - ABD的体积为长方体的体积减去四个全等的三棱锥的体积,故$V_{C - ABD}=2\sqrt{7}-4×\frac{1}{3}×\frac{1}{2}×\sqrt{2}×\sqrt{2}×\sqrt{7}=\frac{2\sqrt{7}}{3},$$V_{P - ABD}=\frac{2}{3}V_{C - ABD}=\frac{4\sqrt{7}}{9}.]$
$6.\sqrt{17} \frac{4\sqrt{7}}{9}[$提示:因为AB = AC =DB = DC = 3,AD = BC = 2,所以将三棱锥的部分侧面展开铺平可得平行四边形ABCD,如图1,
在△ADC中,AD = 2,AC = DC = 3,由余弦定理可得$\cos\angle ADC=\frac{1}{3},$|$\overrightarrow{DB}$|=|$\overrightarrow{DA}+\overrightarrow{DC}$|$=\sqrt{\overrightarrow{DA}^{2}+\overrightarrow{DC}^{2}+2\overrightarrow{DA}·\overrightarrow{DC}}=\sqrt{17},$而$PD + PB≥DB=\sqrt{17},$所以PD + PB的最小值为$\sqrt{17}.$当AP = 2PC时,易知$V_{P - ABD}=\frac{2}{3}V_{C - ABD}.$因为AB = AC = DB = DC = 3,AD = BC = 2,所以可以构造如图2所示的长方体.设长方体的长、宽、高分别为a,b,c,则$\begin{cases}a^{2}+c^{2}=DB^{2}=9\\a^{2}+b^{2}=DC^{2}=9\end{cases},$解得$\begin{cases}a=\sqrt{7}\\b=c=\sqrt{2}\end{cases},$


所以长方体的长为$\sqrt{7},$宽和高均为$\sqrt{2},$观察图形可知,三棱锥C - ABD的体积为长方体的体积减去四个全等的三棱锥的体积,故$V_{C - ABD}=2\sqrt{7}-4×\frac{1}{3}×\frac{1}{2}×\sqrt{2}×\sqrt{2}×\sqrt{7}=\frac{2\sqrt{7}}{3},$$V_{P - ABD}=\frac{2}{3}V_{C - ABD}=\frac{4\sqrt{7}}{9}.]$
7.【题型一】某广场设置了一些石凳供大家休息,这些石凳是由正方体截去八个一样大的正三棱锥得到的(如图).则该几何体共有

14
个面;如果被截正方体的棱长是$50\mathrm{cm}$,那么石凳的表面积是$(7500+2500\sqrt{3})$
$\mathrm{cm}^2$.
答案:
$7.14(7500+2500\sqrt{3})[$提示:由题意知,截去的八个正三棱锥是全等的正三棱锥,8个底面三角形,再加上6个小正方形,所以该几何体共有14个面;如果被截正方体的棱长是50cm,那么石凳的表面积是$S_{表}=8×\frac{1}{2}×25\sqrt{2}×25\sqrt{2}×\sin60^{\circ}+6×25\sqrt{2}×25\sqrt{2}=7500+2500\sqrt{3}(cm^{2}).]$
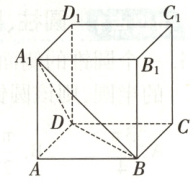
8.【题型二】如图,正方体$ABCD - A_1B_1C_1D_1$的棱长为$a$,过顶点$B$,$D$,$A_1$截下一个三棱锥.
(1)求剩余部分的体积;
(2)求三棱锥$A - A_1BD$的体积及高.
(1)求剩余部分的体积;
(2)求三棱锥$A - A_1BD$的体积及高.

答案:
8.解:
(1)由题意,正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$的棱长为a,则正方体的体积为$V_{1}=a^{3},$又三棱锥$A_{1}-ABD$的体积$V_{A_{1}-ABD}=\frac{1}{3}· S_{\triangle ABD}· A_{1}A=\frac{1}{3}×\frac{1}{2}×AB×AD×A_{1}A=\frac{1}{6}a^{3},$所以剩余部分的体积$V = V_{1}-V_{A_{1}-ABD}=a^{3}-\frac{1}{6}a^{3}=\frac{5}{6}a^{3}。$
(2)由
(1)知$V_{A - A_{1}BD}=V_{A_{1}-ABD}=\frac{1}{6}a^{3},$设三棱锥$A - A_{1}BD$的高为h,$△A_{1}BD$是等边三角形,边长为$\sqrt{2}a,$即$S_{\triangle A_{1}BD}=\frac{1}{2}×(\sqrt{2}a)^{2}×\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2}a^{2},$则$V_{A - A_{1}BD}=\frac{1}{3}· S_{\triangle A_{1}BD}· h=\frac{1}{3}×\frac{\sqrt{3}}{2}a^{2}h=\frac{\sqrt{3}}{6}a^{2}h,$即$\frac{\sqrt{3}}{6}a^{2}h=\frac{1}{6}a^{3},$解得$h=\frac{\sqrt{3}}{3}a,$故三棱锥$A - A_{1}BD$的体积为$\frac{1}{6}a^{3},$高为$\frac{\sqrt{3}}{3}a。$
(1)由题意,正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$的棱长为a,则正方体的体积为$V_{1}=a^{3},$又三棱锥$A_{1}-ABD$的体积$V_{A_{1}-ABD}=\frac{1}{3}· S_{\triangle ABD}· A_{1}A=\frac{1}{3}×\frac{1}{2}×AB×AD×A_{1}A=\frac{1}{6}a^{3},$所以剩余部分的体积$V = V_{1}-V_{A_{1}-ABD}=a^{3}-\frac{1}{6}a^{3}=\frac{5}{6}a^{3}。$
(2)由
(1)知$V_{A - A_{1}BD}=V_{A_{1}-ABD}=\frac{1}{6}a^{3},$设三棱锥$A - A_{1}BD$的高为h,$△A_{1}BD$是等边三角形,边长为$\sqrt{2}a,$即$S_{\triangle A_{1}BD}=\frac{1}{2}×(\sqrt{2}a)^{2}×\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2}a^{2},$则$V_{A - A_{1}BD}=\frac{1}{3}· S_{\triangle A_{1}BD}· h=\frac{1}{3}×\frac{\sqrt{3}}{2}a^{2}h=\frac{\sqrt{3}}{6}a^{2}h,$即$\frac{\sqrt{3}}{6}a^{2}h=\frac{1}{6}a^{3},$解得$h=\frac{\sqrt{3}}{3}a,$故三棱锥$A - A_{1}BD$的体积为$\frac{1}{6}a^{3},$高为$\frac{\sqrt{3}}{3}a。$
在棱长为$a$的正方体中,连接相邻面的中心,以这些线段为棱的八面体的体积为
(
A.$\frac{a^3}{3}$
B.$\frac{a^3}{4}$
C.$\frac{a^3}{6}$
D.$\frac{a^3}{12}$
(
C
)A.$\frac{a^3}{3}$
B.$\frac{a^3}{4}$
C.$\frac{a^3}{6}$
D.$\frac{a^3}{12}$
答案:
C[提示:此八面体可以分割成两个正四棱锥,且正四棱锥的底面是一个边长为$\sqrt{(\frac{a}{2})^{2}+(\frac{a}{2})^{2}}=\frac{\sqrt{2}}{2}a$的正方形,故该八面体的体积为$2(\frac{1}{3}·\frac{1}{2}a^{2}·\frac{a}{2})=\frac{1}{6}a^{3}.]$
查看更多完整答案,请扫码查看


