《2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版》

1. 在四边形 $ABCD$ 中，$AB = DC = (3, \sqrt{3})$，且满足$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|} + \frac{\overrightarrow{AD}}{|\overrightarrow{AD}|} = \frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$，则$|\overrightarrow{AC}|$等于 (D)

A.2
B.6
C.$\sqrt{3}$
D.$2\sqrt{3}$

答案：
1.D[提示:如图所示，$\because \frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}+\frac{\overrightarrow{AD}}{|\overrightarrow{AD}|}=\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$，$\therefore \overrightarrow{AC}$是$\angle BAD$的平分线.由已知得$\left(\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}+\frac{\overrightarrow{AD}}{|\overrightarrow{AD}|}\right)^2=\left(\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}\right)^2$，$\therefore 1 + 1 + 2\cos\angle BAD = 1$，$\therefore \cos\angle BAD = -\frac{1}{2}$，$\therefore \angle DAB = 120°$，$\therefore \angle DAC = 60°$.$\because \overrightarrow{AB} = \overrightarrow{DC}$，$\therefore$四边形$ABCD$是平行四边形，$\therefore \angle ADC = 60°$，$\therefore \triangle ACD$是等边三角形，$\therefore |\overrightarrow{AC}| = |\overrightarrow{DC}| = \sqrt{9 + 3} = 2\sqrt{3}$.

]

2. 已知 $\boldsymbol{a}, \boldsymbol{b}$ 均为单位向量，且 $\boldsymbol{a}$ 与 $\boldsymbol{b}$ 的夹角为 $60°$，则$|\boldsymbol{a} - 2\boldsymbol{b}|$等于 (D)

A.3
B.$\sqrt{2}$
C.2
D.$\sqrt{3}$

答案： 2.D[提示:由题意可得$|\boldsymbol{a}-2\boldsymbol{b}| = \sqrt{(\boldsymbol{a}-2\boldsymbol{b})^2} = \sqrt{\boldsymbol{a}^2 - 4\boldsymbol{a}·\boldsymbol{b} + 4\boldsymbol{b}^2} = \sqrt{1^2 - 4×1×1×\cos60° + 4×1^2} = \sqrt{3}$.]

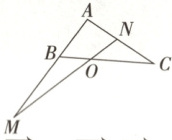
3. (教材改编题) 如图，在$\triangle ABC$中，点$O$是线段$BC$上靠近点$B$的三等分点，过点$O$的直线分别交直线$AB, AC$于点$M, N$. 设$\overrightarrow{AB} = m\overrightarrow{AM}, \overrightarrow{AC} =n\overrightarrow{AN}$, 则$2m + n$的值为 (C)


A.1
B.2
C.3
D.4

答案：
3.C[提示:如图，连接$AO$，因为点$O$是线段$BC$上靠近点$B$的三等分点，所以$\overrightarrow{CO} = 2\overrightarrow{OB}$，所以$\overrightarrow{AO} - \overrightarrow{AC} = 2(\overrightarrow{AB} - \overrightarrow{AO})$，所以$\overrightarrow{AO} = \frac{2}{3}\overrightarrow{AB} + \frac{1}{3}\overrightarrow{AC}$，又因为$\overrightarrow{AB} = \boldsymbol{m}\overrightarrow{AM}$，$\overrightarrow{AC} = \boldsymbol{n}\overrightarrow{AN}$，所以$\overrightarrow{AO} = \frac{2}{3}\boldsymbol{m}\overrightarrow{AM} + \frac{1}{3}\boldsymbol{n}\overrightarrow{AN}$，因为$M$，$N$，$O$三点共线，所以$\frac{2}{3}\boldsymbol{m} + \frac{1}{3}\boldsymbol{n} = 1$，所以$2\boldsymbol{m} + \boldsymbol{n} = 3$.

]

4. 已知向量 $\overrightarrow{OA}, \overrightarrow{OB}$ 满足 $\overrightarrow{OA} · \overrightarrow{OB} = 0$，点 $C$ 在以点 $O$ 为圆心的劣弧 $\overset{\frown}{AB}$ 上，$\overrightarrow{OC} = x\overrightarrow{OA} + y\overrightarrow{OB}$，则 $2x + y$ 的最大值为 (D)

A.1
B.$\sqrt{2}$
C.2
D.$\sqrt{5}$

答案： 4.D[提示:$\because \overrightarrow{OA}·\overrightarrow{OB} = 0$，点$C$在以点$O$为圆心的劣弧$\widehat{AB}$上，$\overrightarrow{OC} = x\overrightarrow{OA} + y\overrightarrow{OB}$，$\therefore \overrightarrow{OC}^2 = (x\overrightarrow{OA} + y\overrightarrow{OB})^2 = x^2\overrightarrow{OA}^2 + y^2\overrightarrow{OB}^2 + 2xy\overrightarrow{OA}·\overrightarrow{OB}$，$\therefore x^2 + y^2 = 1$，设$x = \cos\theta$，$y = \sin\theta$，$\theta \in \left[0,\frac{\pi}{2}\right]$，则$2x + y = 2\cos\theta + \sin\theta = \sqrt{5}\sin(\theta + \alpha)$，且$\sin\alpha = \frac{2\sqrt{5}}{5}$，$\cos\alpha = \frac{\sqrt{5}}{5}$，$\alpha \in \left(0,\frac{\pi}{2}\right)$.$\because 0 ＜ \theta + \alpha ＜ \pi$，$\therefore$当$\theta + \alpha = \frac{\pi}{2}$时，$2x + y = \sqrt{5}\sin(\theta + \alpha)$有最大值，为$\sqrt{5}$.]

5. (教材改编题) 在 $\triangle ABC$ 中，$P_1, P_2, P_3$ 满足$\overrightarrow{AP_1} = \alpha \left( \frac{\overrightarrow{AB}}{|\overrightarrow{AB}|} + \frac{\overrightarrow{AC}}{|\overrightarrow{AC}|} \right), \overrightarrow{AP_2} = \beta \left( \frac{\overrightarrow{AB}}{|\overrightarrow{AB}| \sin B} +\frac{\overrightarrow{AC}}{|\overrightarrow{AC}| \sin C} \right), \overrightarrow{AP_3} = \gamma \left( \frac{\overrightarrow{AB}}{|\overrightarrow{AB}| \cos B} + \frac{\overrightarrow{AC}}{|\overrightarrow{AC}| \cos C} \right)$，则 $P_1, P_2, P_3$ 的轨迹一定分别经过 $\triangle ABC$ 的 (A)

A.内心、重心、垂心
B.重心、内心、垂心
C.内心、垂心、重心
D.重心、垂心、内心

答案：
5.A[提示:因为$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|} + \frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$表示在$\angle BAC$平分线上的向量，又$\overrightarrow{AP_1} = \alpha\left(\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|} + \frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}\right)$，所以$P_1$的轨迹经过$\triangle ABC$的内心；由正弦定理可得$|\overrightarrow{AB}|\sin B = |\overrightarrow{AC}|\sin C$，可得$|\overrightarrow{AB}|\sin B = |\overrightarrow{AC}|\sin C = \boldsymbol{m}(\boldsymbol{m} ＞ 0)$，由$\overrightarrow{AP_2} = \beta\left(\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|\sin B} + \frac{\overrightarrow{AC}}{|\overrightarrow{AC}|\sin C}\right)$，可得$\overrightarrow{AP_2} = \frac{\beta}{\boldsymbol{m}}(\overrightarrow{AB} + \overrightarrow{AC})$，设$BC$的中点为$D$，则$\overrightarrow{AP_2} = \frac{2\beta}{\boldsymbol{m}}\overrightarrow{AD}$，所以$P_2$的轨迹经过$\triangle ABC$的重心.因为$\overrightarrow{AP_3} = \gamma\left(\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|\cos B} + \frac{\overrightarrow{AC}}{|\overrightarrow{AC}|\cos C}\right)$，所以$\overrightarrow{AP_3}·\overrightarrow{BC} = \gamma\left(\frac{\overrightarrow{AB}·\overrightarrow{BC}}{|\overrightarrow{AB}|\cos B} + \frac{\overrightarrow{AC}·\overrightarrow{BC}}{|\overrightarrow{AC}|\cos C}\right) = \gamma\left(\frac{|\overrightarrow{AB}|·|\overrightarrow{BC}|\cos(\pi - B)}{|\overrightarrow{AB}|\cos B} + \frac{|\overrightarrow{AC}|·|\overrightarrow{BC}|\cos C}{|\overrightarrow{AC}|\cos C}\right) = \gamma(-|\overrightarrow{BC}| + |\overrightarrow{BC}|) = 0$，所以$\overrightarrow{AP_3} \perp \overrightarrow{BC}$，所以$P_3$的轨迹经过$\triangle ABC$的垂心.

]

6. 已知平面向量 $\boldsymbol{a}, \boldsymbol{b}$ 满足 $\boldsymbol{a} = (-1, 2)$，$|\boldsymbol{b}| =\sqrt{10}$，$|\boldsymbol{a} - \boldsymbol{b}| = \sqrt{5}$，则 $\boldsymbol{a}$ 与 $\boldsymbol{b}$ 的夹角为 (B)

A.$\frac{\pi}{6}$
B.$\frac{\pi}{4}$
C.$\frac{\pi}{3}$
D.$\frac{\pi}{12}$

答案： 6.B[提示:设向量$\boldsymbol{a}$与$\boldsymbol{b}$的夹角为$\theta$，$\because \boldsymbol{a} = (-1,2)$，$\therefore |\boldsymbol{a}| = \sqrt{5}$.$\because |\boldsymbol{b}| = \sqrt{10}$，$|\boldsymbol{a} - \boldsymbol{b}| = \sqrt{5}$，$\therefore |\boldsymbol{a} - \boldsymbol{b}|^2 = |\boldsymbol{a}|^2 + |\boldsymbol{b}|^2 - 2\boldsymbol{a}·\boldsymbol{b} = |\boldsymbol{a}|^2 + |\boldsymbol{b}|^2 - 2|\boldsymbol{a}|·|\boldsymbol{b}|\cos\theta = 5 + 10 - 2×\sqrt{5}×\sqrt{10}×\cos\theta = 15 - 10\sqrt{2}\cos\theta = 5$，解得$\cos\theta = \frac{\sqrt{2}}{2}$，$\because 0 \leqslant \theta \leqslant \pi$，$\therefore \theta = \frac{\pi}{4}$.]

7. [多选] 已知 $\boldsymbol{a}$ 与 $\boldsymbol{b}$ 均为单位向量，其夹角为 $\theta$，则下列命题中，是真命题的是 (AD)

A.若 $|\boldsymbol{a} + \boldsymbol{b}| ＞ 1$，则 $\theta \in \left[0, \frac{2\pi}{3}\right)$
B.若 $|\boldsymbol{a} + \boldsymbol{b}| ＞ 1$，则 $\theta \in \left(\frac{2\pi}{3}, \pi\right]$
C.若 $|\boldsymbol{a} - \boldsymbol{b}| ＞ 1$，则 $\theta \in \left[0, \frac{\pi}{3}\right)$
D.若 $|\boldsymbol{a} - \boldsymbol{b}| ＞ 1$，则 $\theta \in \left(\frac{\pi}{3}, \pi\right]$

答案： 7.AD[提示:由$|\boldsymbol{a} + \boldsymbol{b}| ＞ 1$得$2 + 2\cos\theta ＞ 1$，即$\cos\theta ＞ -\frac{1}{2}$.又$\theta \in [0,\pi]$，所以$\theta \in \left[0,\frac{2\pi}{3}\right)$，故A正确，B错误；由$|\boldsymbol{a} - \boldsymbol{b}| ＞ 1$得$2 - 2\cos\theta ＞ 1$，即$\cos\theta ＜ \frac{1}{2}$.又$\theta \in [0,\pi]$，所以$\theta \in \left(\frac{\pi}{3},\pi\right]$，故C错误，D正确.]

8. (教材改编题) 若同一平面内的三个力 $\boldsymbol{F}_1, \boldsymbol{F}_2, \boldsymbol{F}_3$ 作用于同一个物体，且该物体处于平衡状态，已知 $|\boldsymbol{F}_1| = 3$，$|\boldsymbol{F}_2| = 4$，且 $\boldsymbol{F}_1$ 与 $\boldsymbol{F}_2$ 的夹角为 $120°$，则力 $\boldsymbol{F}_3$ 的大小为 (D)

A.37
B.$\sqrt{37}$
C.13
D.$\sqrt{13}$

答案： 8.D[提示:由题意可知，$\boldsymbol{F}_3 = -(\boldsymbol{F}_1 + \boldsymbol{F}_2)$，所以$|\boldsymbol{F}_3|^2 = \boldsymbol{F}_3^2 = (\boldsymbol{F}_1 + \boldsymbol{F}_2)^2 = \boldsymbol{F}_1^2 + 2\boldsymbol{F}_1·\boldsymbol{F}_2 + \boldsymbol{F}_2^2 = 3^2 + 2×3×4×\cos120° + 4^2 = 13$，所以$|\boldsymbol{F}_3| = \sqrt{13}$，即力$\boldsymbol{F}_3$的大小为$\sqrt{13}$.]

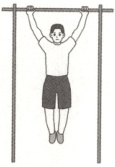
1.【题型二】体育锻炼是青少年生活学习中非常重要的组成部分. 某学生做引体向上运动，处于如图所示的平衡状态，若两只胳膊的夹角为 $60°$，每只胳膊的拉力大小均为 $300\ N$，则该学生的体重约为(参考数据：取重力加速度大小为 $g \approx 10\ m/s^2$，$\sqrt{3} \approx 1.732$) (A)


A.52 kg
B.60 kg
C.70 kg
D.102 kg

答案： 1.A[提示:设两只胳膊的拉力分别为$\boldsymbol{f}_1$，$\boldsymbol{f}_2$，且$|\boldsymbol{f}_1| = |\boldsymbol{f}_2| = 300\ N$，$(\boldsymbol{f}_1,\boldsymbol{f}_2) = 60°$，则$|\boldsymbol{f}_1 + \boldsymbol{f}_2| = \sqrt{\boldsymbol{f}_1^2 + \boldsymbol{f}_2^2 + 2\boldsymbol{f}_1·\boldsymbol{f}_2} = \sqrt{90000 + 90000 + 2×300×300\cos60°} = 300\sqrt{3} \approx 520\ ( N)$，所以该学生的体重$\boldsymbol{m} \approx 52\ kg$.]