《2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版》

4.【题型三】(2025·黑龙江牡丹江市名校协作体高一下月考)在正方形$ABCD$中，$E, F$分别为$BC, CD$的中点，则下列等式不正确的是 (C)

A.$\overrightarrow{AC} = \overrightarrow{AF} + \frac{1}{2}\overrightarrow{AB}$
B.$\overrightarrow{AC} = \overrightarrow{AE} + \frac{1}{2}\overrightarrow{AD}$
C.$\overrightarrow{AC} = \frac{1}{3}\overrightarrow{AE} + \frac{2}{3}\overrightarrow{AF}$
D.$\overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{AD}$

答案：
4.C[提示:由题意可得$\overrightarrow{AC}$ = $\overrightarrow{AF}$ + $\overrightarrow{FC}$ = $\overrightarrow{AF}$ + $\frac{1}{2}$$\overrightarrow{DC}$ = $\overrightarrow{AF}$ + $\frac{1}{2}$$\overrightarrow{AB}$,A正确;由E为BC的中点及向量加法的三角形法则可得$\overrightarrow{AC}$ = $\overrightarrow{AE}$ + $\overrightarrow{EC}$ = $\overrightarrow{AE}$ + $\frac{1}{2}$$\overrightarrow{BC}$ = $\overrightarrow{AE}$ + $\frac{1}{2}$($\overrightarrow{AC}$ - $\overrightarrow{AB}$) = $\overrightarrow{AE}$ + $\frac{1}{2}$$\overrightarrow{AD}$,由F为DC的中点及向量加法的三角形法则可得$\overrightarrow{AF}$ = $\overrightarrow{AD}$ + $\overrightarrow{DF}$ = $\overrightarrow{AD}$ + $\frac{1}{2}$$\overrightarrow{DC}$ = $\overrightarrow{AD}$ + $\frac{1}{2}$$\overrightarrow{AB}$,因为$\overrightarrow{AB}$ + $\overrightarrow{AD}$ = $\overrightarrow{AC}$,$\overrightarrow{AB}$ + $\overrightarrow{AD}$ = $\frac{2}{3}$($\overrightarrow{AE}$ + $\overrightarrow{AF}$),从而有$\overrightarrow{AC}$ = $\overrightarrow{AB}$ + $\overrightarrow{AD}$ = $\frac{2}{3}$$\overrightarrow{AE}$ + $\frac{2}{3}$$\overrightarrow{AF}$,故C错误,D正确.

5.【题型一】(2025·黑龙江省实验中学高一下段考)设$\boldsymbol{e_1}, \boldsymbol{e_2}$是空间中两个不共线的向量，已知$\overrightarrow{AB} = 3\boldsymbol{e_1} + k\boldsymbol{e_2}, \overrightarrow{CB} = \boldsymbol{e_1} + 2\boldsymbol{e_2}, \overrightarrow{CD} = 2\boldsymbol{e_1} - \boldsymbol{e_2}$，且$A, B, D$三点共线，则$k$的值为 (D)

A.3
B.$-3$
C.9
D.$-9$

答案： 5.D[提示:因为$\overrightarrow{BD}$ = $\overrightarrow{CD}$ - $\overrightarrow{CB}$ = e₁ - 3e₂,$\overrightarrow{AB}$ = 3e₁ + ke₂,且A,B,D三点共线,所以$\overrightarrow{AB}$ = λ$\overrightarrow{BD}$,即3e₁ + ke₂ = λ(e₁ - 3e₂),所以λ = 3,k = -9.]

6.【题型二】如图所示，在$\triangle ABC$中，$\overrightarrow{AD} = \frac{1}{2}\overrightarrow{AB}$，$\overrightarrow{AE} = \frac{1}{3}\overrightarrow{AC}$，$CD$与$BE$交于点$P$，若$\overrightarrow{AP} = \lambda\overrightarrow{AB} + \mu\overrightarrow{AC}$，则$\lambda + \mu$的值为$\frac{3}{5}$

答案： 6.$\frac{3}{5}$[提示:
∵$\overrightarrow{AD}$ = $\frac{1}{2}$$\overrightarrow{AB}$,$\overrightarrow{AE}$ = $\frac{1}{3}$$\overrightarrow{AC}$,又$\overrightarrow{AP}$ = λ$\overrightarrow{AB}$ + μ$\overrightarrow{AC}$ = 2λ$\overrightarrow{AD}$ + 3μ$\overrightarrow{AE}$,
∵E,P,B三点共线,D,P,C三点共线,
∴$\begin{cases} 2\lambda + \mu = 1 \\ \lambda + 3\mu = 1 \end{cases}$,
∴λ = $\frac{2}{5}$,μ = $\frac{1}{5}$,
∴λ + μ = $\frac{3}{5}$.]

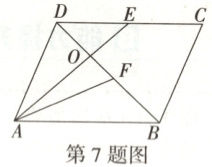
7.【题型二】如图所示，在平行四边形$ABCD$中，$E$是$CD$的中点，$F$是线段$BD$上的动点，若$\overrightarrow{AF} = x\overrightarrow{AE} + y\overrightarrow{DC} (x ＞ 0, y ＞ 0)$，则$\frac{2 - 3x}{2y^2 + 1}$的最大值为$\frac{\sqrt{2}}{2}$.

答案： 7.$\frac{\sqrt{2}}{2}$[提示:$\overrightarrow{AE}$ = $\overrightarrow{AD}$ + $\overrightarrow{DE}$ = $\overrightarrow{AD}$ + $\frac{1}{2}$$\overrightarrow{AB}$,$\overrightarrow{DC}$ = $\overrightarrow{AB}$,由$\overrightarrow{AF}$ = x$\overrightarrow{AE}$ + y$\overrightarrow{DC}$(x ＞ 0,y ＞ 0),可得$\overrightarrow{AF}$ = x($\overrightarrow{AD}$ + $\frac{1}{2}$$\overrightarrow{AB}$) + y$\overrightarrow{AB}$ = x$\overrightarrow{AD}$ + ($\frac{1}{2}$x + y)$\overrightarrow{AB}$,由于B,D,F三点共线,则x + $\frac{1}{2}$x + y = $\frac{3}{2}$x + y = 1,于是$\frac{2 - 3x}{2y^2 + 1}$ + $\frac{2y}{2y^2 + 1}$ = $\frac{2y}{2y + \frac{y}{2}}$ = $\frac{2}{2\sqrt{2}}$ = $\frac{\sqrt{2}}{2}$,当且仅当y = $\frac{\sqrt{2}}{2}$时取等号,则$\frac{2 - 3x}{2y^2 + 1}$的最大值为$\frac{\sqrt{2}}{2}$.]

8.【题型一、二】设$\boldsymbol{e_1}, \boldsymbol{e_2}$是不共线的非零向量，且$\boldsymbol{a} = \boldsymbol{e_1} - 2\boldsymbol{e_2}, \boldsymbol{b} = \boldsymbol{e_1} + 3\boldsymbol{e_2}$.
(1)求证$\boldsymbol{a}, \boldsymbol{b}$可以作为一组基底；
(2)若$4\boldsymbol{e_1} - 3\boldsymbol{e_2} = \lambda\boldsymbol{a} + \mu\boldsymbol{b}$，求$\lambda, \mu$的值.

答案： 8.
(1)证明:假设a//b,则e₁ - 2e₂ = λ(e₁ + 3e₂),故$\begin{cases} 1 = \lambda \\ -2 = 3\lambda \end{cases}$显然该方程组无解,故a与b不共线,所以a,b可以作为一组基底.
(2)解:由4e₁ - 3e₂ = λa + μb得4e₁ - 3e₂ = λ(e₁ - 2e₂) + μ(e₁ + 3e₂) = (λ + μ)e₁ + (3μ - 2λ)e₂,所以$\begin{cases} \lambda + \mu = 4 \\ 3\mu - 2\lambda = -3 \end{cases}$解得$\begin{cases} \lambda = 3 \\ \mu = 1 \end{cases}$.

9.【题型三】(2025·黑龙江哈尔滨松雷中学高一下月考)如图，在等边三角形$ABC$中，$AB = 3$，点$O$在边$BC$上，且$\overrightarrow{OC} = 2\overrightarrow{BO}$，过点$O$的直线分别交射线$AB, AC$于不同的两点$M, N$.
(1)设$\overrightarrow{AB} = \boldsymbol{a}, \overrightarrow{AC} = \boldsymbol{b}$，试用$\boldsymbol{a}, \boldsymbol{b}$表示$\overrightarrow{AO}$；
(2)求$\cos \angle AOB$的值；
(3)设$\overrightarrow{AB} = m\overrightarrow{AM}, \overrightarrow{AC} = n\overrightarrow{AN}$，求$\frac{n + 1}{m} + \frac{2}{n}$的最小值.

答案： 9.解:
(1)根据题意可知等边三角形ABC中,AB = 3,点O在边BC上,且OC = 2BO,过点O的直线分别交射线AB,AC于不同的两点M,N,$\overrightarrow{AB}$ = a,$\overrightarrow{AC}$ = b,
∴$\overrightarrow{CO}$ = $\frac{2}{3}$$\overrightarrow{CB}$ = $\frac{2}{3}$$\overrightarrow{AB}$ - $\frac{2}{3}$$\overrightarrow{AC}$ = $\frac{2}{3}$a - $\frac{2}{3}$b,
∴$\overrightarrow{AO}$ = $\overrightarrow{CO}$ - $\overrightarrow{CA}$ = $\frac{2}{3}$a - $\frac{2}{3}$b - (-b) = $\frac{2}{3}$a + $\frac{1}{3}$b,且|a| = |b| = 3,a·b = $\frac{9}{2}$,
∴|$\overrightarrow{OB}$| = 1,|$\overrightarrow{OA}$| = $\sqrt{\frac{4}{9}a^2 + \frac{4}{9}a · b + \frac{1}{9}b^2}$ = $\sqrt{\frac{4}{9} × 9 + \frac{1}{9} × \frac{9}{2} + \frac{1}{9} × 9}$ = $\sqrt{7}$,$\overrightarrow{OB}$·$\overrightarrow{OA}$ = -$\frac{1}{9}$a² + $\frac{1}{9}$b² + $\frac{2}{9}$a·b = $\frac{2}{9}$×9 + $\frac{1}{9}$×$\frac{9}{2}$×9 = -$\frac{9}{2}$,
∴cos∠AOB = $\frac{\overrightarrow{OB} · \overrightarrow{OA}}{|\overrightarrow{OB}| · |\overrightarrow{OA}|}$ = $\frac{-\frac{9}{2}}{\sqrt{7} × 1}$ = -$\frac{\sqrt{7}}{14}$.
(3)
∵$\overrightarrow{AO}$ = $\frac{2}{3}$$\overrightarrow{AB}$ + $\frac{1}{3}$$\overrightarrow{AC}$ = $\frac{2m}{3}$$\overrightarrow{AM}$ + $\frac{n}{3}$$\overrightarrow{AN}$,且M,N,O三点共线,
∴$\frac{2m}{3}$ + $\frac{n}{3}$ = 1,且m,n ＞ 0,
∴$\frac{2}{n}$ + $\frac{n}{m}$ = $\frac{4m}{3n}$ + $\frac{4n}{3m}$ + $\frac{4m}{3m}$ + $\frac{4n}{3n}$ ≥ 2×$\frac{4}{3}$ + $\frac{4}{3}$ = 4.当且仅当$\frac{4m}{3n}$ = $\frac{4n}{3m}$,即m = n = 1时等号成立,
∴$\frac{n + 1}{m}$ + $\frac{n}{m}$的最小值为4.

1.(2025·吉林长春东北师大附中高一下段考)如图，在$\triangle ABM$中，$BM = 3CM$，$\overrightarrow{AN} = \frac{2}{7}\overrightarrow{AM}$，若$\overrightarrow{AN} = \lambda\overrightarrow{AB} + \mu\overrightarrow{AC}$，则$\lambda + \mu$等于 (D)

A.$-\frac{1}{7}$
B.$\frac{1}{7}$
C.$-\frac{2}{7}$
D.$\frac{2}{7}$

答案： 1.D[提示:$\overrightarrow{AN}$ = $\frac{2}{7}$$\overrightarrow{AM}$ = $\frac{2}{7}$($\overrightarrow{AB}$ + $\overrightarrow{BM}$) = $\frac{2}{7}$$\overrightarrow{AB}$ + $\frac{2}{7}$×$\frac{3}{2}$×(-$\overrightarrow{BC}$) = $\frac{2}{7}$$\overrightarrow{AB}$ - $\frac{3}{7}$($\overrightarrow{AC}$ - $\overrightarrow{AB}$) = $\frac{3}{7}$$\overrightarrow{AC}$ - $\frac{1}{7}$$\overrightarrow{AB}$,故λ + μ = -$\frac{1}{7}$ - $\frac{3}{7}$ = -$\frac{2}{7}$.]

2.(2025·黑龙江哈尔滨三中高一下月考)在$\triangle ABC$中，已知$AB = 2, AC = 3$，若点$O$为$\triangle ABC$的外心，点$M$满足$2\overrightarrow{BM} = \overrightarrow{MC}$，则$\overrightarrow{AO} · \overrightarrow{AM}$等于 (A)

A.$\frac{17}{6}$
B.$\frac{5}{2}$
C.$\frac{11}{3}$
D.3

答案： 2.A[提示:已知2$\overrightarrow{BM}$ = $\overrightarrow{MC}$,即$\overrightarrow{BM}$ = $\frac{1}{3}$$\overrightarrow{BC}$,根据向量加法的三角形法则可得$\overrightarrow{AM}$ = $\overrightarrow{AB}$ + $\overrightarrow{BM}$ = $\overrightarrow{AB}$ + $\frac{1}{3}$$\overrightarrow{BC}$ = $\overrightarrow{AB}$ + $\frac{1}{3}$($\overrightarrow{AC}$ - $\overrightarrow{AB}$) = $\frac{2}{3}$$\overrightarrow{AB}$ + $\frac{1}{3}$$\overrightarrow{AC}$,设D为AB的中点,因为点O为△ABC的外心,所以OD⊥AB,则$\overrightarrow{OD}$·$\overrightarrow{AB}$ = 0,又因为$\overrightarrow{AO}$·$\overrightarrow{AB}$ = ($\overrightarrow{AD}$ + $\overrightarrow{DO}$)·$\overrightarrow{AB}$ = $\overrightarrow{AD}$·$\overrightarrow{AB}$ + $\overrightarrow{DO}$·$\overrightarrow{AB}$,$\overrightarrow{DO}$·$\overrightarrow{AB}$ = 0,且$\overrightarrow{AD}$ = $\frac{1}{2}$$\overrightarrow{AB}$,所以$\overrightarrow{AO}$·$\overrightarrow{AB}$ = $\frac{1}{2}$$\overrightarrow{AB}$·$\overrightarrow{AB}$ = $\frac{1}{2}$|$\overrightarrow{AB}$|²,因为AB = 2,所以$\overrightarrow{AO}$·$\overrightarrow{AB}$ = $\frac{1}{2}$×2² = 2,同理,设E为AC的中点,则$\overrightarrow{AO}$·$\overrightarrow{AC}$ = ($\overrightarrow{AE}$ + $\overrightarrow{EO}$)·$\overrightarrow{AC}$ = $\overrightarrow{AE}$·$\overrightarrow{AC}$ + $\overrightarrow{EO}$·$\overrightarrow{AC}$,因为$\overrightarrow{EO}$·$\overrightarrow{AC}$ = 0,且$\overrightarrow{AE}$ = $\frac{1}{2}$$\overrightarrow{AC}$,所以$\overrightarrow{AO}$·$\overrightarrow{AC}$ = $\frac{1}{2}$$\overrightarrow{AC}$·$\overrightarrow{AC}$ = $\frac{1}{2}$|$\overrightarrow{AC}$|²,因为AC = 3,所以$\overrightarrow{AO}$·$\overrightarrow{AC}$ = $\frac{1}{2}$×3² = $\frac{9}{2}$,将$\overrightarrow{AM}$ = $\frac{2}{3}$$\overrightarrow{AB}$ + $\frac{1}{3}$$\overrightarrow{AC}$代入$\overrightarrow{AO}$·$\overrightarrow{AM}$可得$\overrightarrow{AO}$·$\overrightarrow{AM}$ = $\frac{2}{3}$$\overrightarrow{AO}$·$\overrightarrow{AB}$ + $\frac{1}{3}$$\overrightarrow{AO}$·$\overrightarrow{AC}$ = $\frac{2}{3}$×2 + $\frac{1}{3}$×$\frac{9}{2}$×$\frac{1}{3}$ = $\frac{4}{3}$ + $\frac{3}{6}$ = $\frac{17}{6}$.]