2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第28页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1.【题型二】(2025·黑龙江哈尔滨九中高一下月考)中国古代四大名楼之首的黄鹤楼位于湖北省武汉市武昌区,因唐代诗人崔颢登楼所题的《黄鹤楼》一诗而名扬四海.如图,某同学为测量黄鹤楼的高度 $MN$,在黄鹤楼的正东方向找到一座建筑物 $AB$,高约为 $26\ m$,在地面上点 $C$ 处($B,C,N$ 三点共线)测得建筑物顶部 $A$、黄鹤楼顶部 $M$ 的仰角分别为 $30^{\circ}$ 和 $45^{\circ}$,在 $A$ 处测得楼顶部 $M$ 的仰角为 $15^{\circ}$,则黄鹤楼的高度约为 (
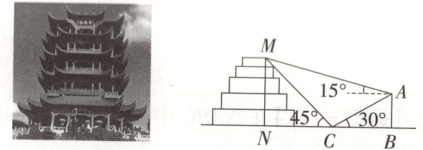
A.$64\ m$
B.$74\ m$
C.$52\ m$
D.$91\ m$
C
)
A.$64\ m$
B.$74\ m$
C.$52\ m$
D.$91\ m$
答案:
1.C[提示:在Rt△ABC中,AC=$\frac{AB}{\sin\angle ACB}$=$\frac{26}{\sin 30°}$,∠ACM = 180° - ∠ACB - ∠MCN = 105°,∠CAM = 15° + 30° = 45°,在△ACM中,∠CMA = 180° - ∠MAC - ∠ACM = 30°,由$\frac{AC}{\sin 30°}$ = $\frac{MC}{\sin 45°}$,得MC = $\frac{AC}{\sin 30°}$·sin 45° = $\frac{26}{\sin^2 30°}$·sin 45° = 52$\sqrt{2}$,在Rt△MNC中,MN = MC·sin 45° = 52 m.]
2.【题型一】某大学校园内有一个“少年湖”,湖的两侧有一个健身房和一个图书馆,如图所示,若设健身房在 $A$ 处,图书馆在 $B$ 处,为测量 $A$,$B$ 两地之间的距离,甲同学选定了与 $A$,$B$ 不共线的 $C$ 处,构成 $\triangle ABC$,以下是测量数据的不同方案:
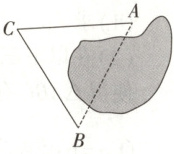
①测量 $\angle A$,$\angle B$,$\angle C$;
②测量 $\angle A$,$\angle B$,$BC$;
③测量 $\angle A$,$AC$,$BC$;
④测量 $\angle C$,$AC$,$BC$.
其中要求能唯一确定 $A$,$B$ 两地之间的距离,甲同学应选择的方案的序号为 (
A.①②
B.②③
C.②④
D.③④

①测量 $\angle A$,$\angle B$,$\angle C$;
②测量 $\angle A$,$\angle B$,$BC$;
③测量 $\angle A$,$AC$,$BC$;
④测量 $\angle C$,$AC$,$BC$.
其中要求能唯一确定 $A$,$B$ 两地之间的距离,甲同学应选择的方案的序号为 (
C
)A.①②
B.②③
C.②④
D.③④
答案:
2.C[提示:①测量∠A,∠B,∠C,知道三个角度值,三角形有无数多组解,不能唯一确定A,B两地之间的距离;②测量∠A,∠B,BC,已知两角及一边,由正弦定理可知,三角形有唯一的解,能唯一确定A,B两地之间的距离;③测量∠A,AC,BC,已知两边及其一边的对角,由正弦定理可知,三角形可能有2个解,不能唯一确定A,B两地之间的距离;④测量∠C,AC,BC,已知两边及夹角,由余弦定理可知,三角形有唯一的解,能唯一确定A,B两地之间的距离.综上所述,能唯一确定A,B两地之间的距离的方案的序号是②④.]
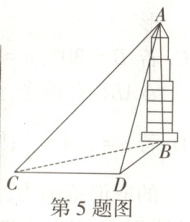
3.【题型二】(2025·黑龙江哈尔滨德强高级中学高一下期中)长庆寺塔,又名“十寺塔”,位于安徽省黄山市歙县的西干披云峰麓,历经 $900$ 多年风雨侵蚀,仍巍然屹立,是中国现存少有的方形佛塔.如图,为测量塔的总高度 $AB$,选取与塔底 $B$ 在同一水平面内的两个测量基点 $C$ 与 $D$,现测得 $\angle BCD = 30^{\circ}$,$\angle BDC = 45^{\circ}$,$CD = 32\sqrt{2}\ m$,在 $C$ 点测得塔顶 $A$ 的仰角为 $60^{\circ}$,则塔的总高度为 (

A.$(96 - 32\sqrt{6})\ m$
B.$(96 - 32\sqrt{3})\ m$
C.$(96\sqrt{2} - 32)\ m$
D.$(96\sqrt{2} - 32\sqrt{6})\ m$
D
)
A.$(96 - 32\sqrt{6})\ m$
B.$(96 - 32\sqrt{3})\ m$
C.$(96\sqrt{2} - 32)\ m$
D.$(96\sqrt{2} - 32\sqrt{6})\ m$
答案:
3.D[提示:设AB = h,则BC = $\frac{h}{\tan 60°}$ = $\frac{h}{\sqrt{3}}$,且∠CBD = 180° - (30° + 45°),所以sin∠CBD = sin(30° + 45°) = sin 30°cos 45° + cos 30°sin 45° = $\frac{\sqrt{2}+\sqrt{6}}{4}$,在△BCD中,由正弦定理得$\frac{CD}{\sin\angle CBD}$ = $\frac{BC}{\sin 45°}$,即$\frac{32\sqrt{2}}{\frac{\sqrt{2}+\sqrt{6}}{4}}$ = $\frac{BC}{\frac{\sqrt{2}}{2}}$,解得BC = 32($\sqrt{6}$ - $\sqrt{2}$),所以h = $\sqrt{3}$BC = 96$\sqrt{2}$ - 32$\sqrt{6}$.]
4.【题型一】海洋蓝洞是地球上罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”,我国拥有世界上最深的海洋蓝洞,现要测量如图所示的蓝洞的口径 $A$,$B$ 两点间的距离,在珊瑚群岛上取两点 $C$,$D$,测得 $CD = 35\ m$,$\angle ADB = 135^{\circ}$,$\angle BDC = \angle DCA = 15^{\circ}$,$\angle ACB = 120^{\circ}$,则 $A$,$B$ 两点间的距离为

35$\sqrt{5}$
$m$.
答案:
4.35$\sqrt{5}$[提示:如图所示,在△BCD中,CD = 35 m,∠BDC = 15°,∠BCD = ∠ACB + ∠DCA = 120° + 15° = 135°,所以∠CBD = 30°,由正弦定理得$\frac{BD}{\sin 135°}$ = $\frac{35}{\sin 30°}$,解得BD = 35$\sqrt{2}$(m),在△ACD中,CD = 35 m,∠DCA = 15°,∠ADC = ∠ADB + ∠BDC = 135° + 15° = 150°,所以∠CAD = 15°,所以AD = CD = 35 m,在△ABD中,由余弦定理得AB² = AD² + BD² - 2AD·BD·cos∠ADB = 35² + (35$\sqrt{2}$)² - 2×35×35$\sqrt{2}$×cos 135° = 35²×5,所以AB = 35$\sqrt{5}$ m,即A,B两点间的距离为35$\sqrt{5}$ m. ]
]
4.35$\sqrt{5}$[提示:如图所示,在△BCD中,CD = 35 m,∠BDC = 15°,∠BCD = ∠ACB + ∠DCA = 120° + 15° = 135°,所以∠CBD = 30°,由正弦定理得$\frac{BD}{\sin 135°}$ = $\frac{35}{\sin 30°}$,解得BD = 35$\sqrt{2}$(m),在△ACD中,CD = 35 m,∠DCA = 15°,∠ADC = ∠ADB + ∠BDC = 135° + 15° = 150°,所以∠CAD = 15°,所以AD = CD = 35 m,在△ABD中,由余弦定理得AB² = AD² + BD² - 2AD·BD·cos∠ADB = 35² + (35$\sqrt{2}$)² - 2×35×35$\sqrt{2}$×cos 135° = 35²×5,所以AB = 35$\sqrt{5}$ m,即A,B两点间的距离为35$\sqrt{5}$ m.
 ]
] 5.【题型二】高中数学兴趣小组计划测量某大厦的高度,选取与底部 $B$ 在同一水平面内的两个基测点 $C$ 与 $D$.如图所示,现测得 $\angle BCD = 15^{\circ}$,$\angle BDC = 120^{\circ}$,$CD = 100$ 米,在点 $C$ 处测得大厦顶 $A$ 的仰角 $\angle ACB = 60^{\circ}$,则该大厦高度 $AB =$
参考数据:$\sqrt{2} \approx 1.414$,$\sqrt{3} \approx 1.732$)
212
米.(精确到 $1$ 米.参考数据:$\sqrt{2} \approx 1.414$,$\sqrt{3} \approx 1.732$)

答案:
5.212[提示:由∠BCD = 15°,∠BDC = 120°,可得∠CBD = 45°,又CD = 100米,由正弦定理可得$\frac{CD}{\sin\angle CBD}$ = $\frac{BC}{\sin\angle BDC}$,即$\frac{100}{\frac{\sqrt{2}}{2}}$ = $\frac{BC}{\frac{\sqrt{3}}{2}}$,可得BC = 50$\sqrt{6}$米,在Rt△ABC中,∠ACB = 60°,所以AB = BC·tan∠ACB = 50$\sqrt{6}$×$\sqrt{3}$ = 150$\sqrt{2}$ ≈ 150×1.414 ≈ 212(米).]
6.【题型三】目前,中国已经建成全球最大的 $5G$ 网络,无论是大山深处还是平原,处处都能见到 $5G$ 基站的身影.如图(1)所示,某同学在一条水平公路上观测对面山顶上的一座 $5G$ 基站 $AB$,已知基站高 $AB = 50\ m$,该同学眼高 $1.5\ m$(眼睛到地面的距离),该同学在初始位置 $C$ 处(眼睛所在位置)测得基站底部 $B$ 的仰角为 $37^{\circ}$,测得基站顶端 $A$ 的仰角为 $45^{\circ}$.

(1)求山高 $BE$(结果保留整数).
(2)如图(2)所示,当该同学面向基站 $AB$ 前行时(保持在同一铅垂面内),记该同学所在位置 $C$ 处(眼睛所在位置)到基站 $AB$ 所在直线的距离 $CD = x\ m$,且记在 $C$ 处观测基站底部 $B$ 的仰角为 $\alpha$,观测基站顶端 $A$ 的仰角为 $\beta$,则当 $x$ 多大时,观测基站的视角 $\angle ACB$ 最大?
参考数据:$\sqrt{2} \approx 1.4$,$\sin 8^{\circ} \approx 0.14$,$\sin 37^{\circ} \approx 0.6$,$\sin 45^{\circ} \approx 0.7$,$\sin 127^{\circ} \approx 0.8$.

(1)求山高 $BE$(结果保留整数).
(2)如图(2)所示,当该同学面向基站 $AB$ 前行时(保持在同一铅垂面内),记该同学所在位置 $C$ 处(眼睛所在位置)到基站 $AB$ 所在直线的距离 $CD = x\ m$,且记在 $C$ 处观测基站底部 $B$ 的仰角为 $\alpha$,观测基站顶端 $A$ 的仰角为 $\beta$,则当 $x$ 多大时,观测基站的视角 $\angle ACB$ 最大?
参考数据:$\sqrt{2} \approx 1.4$,$\sin 8^{\circ} \approx 0.14$,$\sin 37^{\circ} \approx 0.6$,$\sin 45^{\circ} \approx 0.7$,$\sin 127^{\circ} \approx 0.8$.
答案:
6.解:
(1)由题意可知,∠BCD = 37°,∠ACD = 45°,∠ACB = 8°,A = 45°,在△ABC中,$\frac{AB}{\sin\angle ACB}$ = $\frac{BC}{\sin A}$,所以BC ≈ $\frac{50×\frac{\sqrt{2}}{2}}{0.14}$ ≈ 250(m),在Rt△BCD中,BD = BCsin∠BCD ≈ 250×0.6 = 150(m),所以山高BE = 150 + 1.5 ≈ 152(m).
(2)由题意知∠ACD = β,∠BCD = α,且0 < α < β < $\frac{\pi}{2}$,则0 < β - α < $\frac{\pi}{2}$,在Rt△BCD中,tanα = $\frac{BD}{CD}$ = $\frac{150}{x}$,在Rt△ACD中,tanβ = $\frac{AD}{CD}$ = $\frac{200}{x}$,则tan∠ACB = tan(β - α) = $\frac{\tan\beta - \tan\alpha}{1 + \tan\beta\tan\alpha}$ = $\frac{\frac{200}{x} - \frac{150}{x}}{1 + \frac{200}{x}×\frac{150}{x}}$ = $\frac{\frac{50x}{x^2 + 30000}}{=\frac{50x}{30000 + x^2}}$ ≤ $\frac{50}{2\sqrt{\frac{30000}{x}}}$ = $\frac{\sqrt{3}}{12}$,当且仅当x = $\frac{30000}{x}$,即x = 100$\sqrt{3}$时,取等号,所以tan∠ACB取得最大值时,x = 100$\sqrt{3}$.又因为0 < ∠ACB < $\frac{\pi}{2}$,所以此时∠ACB最大,即当x = 100$\sqrt{3}$时,∠ACB最大.
(1)由题意可知,∠BCD = 37°,∠ACD = 45°,∠ACB = 8°,A = 45°,在△ABC中,$\frac{AB}{\sin\angle ACB}$ = $\frac{BC}{\sin A}$,所以BC ≈ $\frac{50×\frac{\sqrt{2}}{2}}{0.14}$ ≈ 250(m),在Rt△BCD中,BD = BCsin∠BCD ≈ 250×0.6 = 150(m),所以山高BE = 150 + 1.5 ≈ 152(m).
(2)由题意知∠ACD = β,∠BCD = α,且0 < α < β < $\frac{\pi}{2}$,则0 < β - α < $\frac{\pi}{2}$,在Rt△BCD中,tanα = $\frac{BD}{CD}$ = $\frac{150}{x}$,在Rt△ACD中,tanβ = $\frac{AD}{CD}$ = $\frac{200}{x}$,则tan∠ACB = tan(β - α) = $\frac{\tan\beta - \tan\alpha}{1 + \tan\beta\tan\alpha}$ = $\frac{\frac{200}{x} - \frac{150}{x}}{1 + \frac{200}{x}×\frac{150}{x}}$ = $\frac{\frac{50x}{x^2 + 30000}}{=\frac{50x}{30000 + x^2}}$ ≤ $\frac{50}{2\sqrt{\frac{30000}{x}}}$ = $\frac{\sqrt{3}}{12}$,当且仅当x = $\frac{30000}{x}$,即x = 100$\sqrt{3}$时,取等号,所以tan∠ACB取得最大值时,x = 100$\sqrt{3}$.又因为0 < ∠ACB < $\frac{\pi}{2}$,所以此时∠ACB最大,即当x = 100$\sqrt{3}$时,∠ACB最大.
查看更多完整答案,请扫码查看


