2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
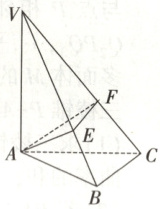
1.《九章算术·商功》:“斜解立方,得两壍堵.斜解壍堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之棊,其形露矣.”即将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图所示的为鳖臑$V-ABC,VA\perp$平面$ABC,AB\perp BC,E,F$分别在棱$VB,VC$上,且$EF\perp VC,AE\perp VB$.若$VA = 4$,则三棱锥$V-AEF$外接球的体积为(
A.$\frac{16}{3}\pi$
B.$4\sqrt{2}\pi$
C.$\frac{32}{3}\pi$
D.$\frac{16\sqrt{2}}{3}\pi$
C
)
A.$\frac{16}{3}\pi$
B.$4\sqrt{2}\pi$
C.$\frac{32}{3}\pi$
D.$\frac{16\sqrt{2}}{3}\pi$
答案:
1.C[提示:$\because VA\perp$平面$ABC$,$BC\subset$平面$ABC$,$\therefore VA\perp BC$,$\because AB\perp BC$,$VA\cap AB=A$,$\therefore BC\perp$平面$VAB$,而$BC\subset$平面$VBC$,可得平面$VBC\perp$平面$VAB$。$\because$平面$VBC\cap$平面$VAB=VB$,$AE\perp VB$,$AE\subset$平面$VAB$,$\therefore AE\perp$平面$VBC$,$\therefore AE\perp VC$。又$EF\perp VC$,$AE\cap EF=E$,$\therefore VC\perp$平面$AEF$,$\therefore VC\perp AF$。$\because AE\perp VB$,$AF\perp VC$,$\therefore VA$为三棱锥$V - AEF$外接球的直径,则半径$R = \frac{1}{2}VA = 2$,$\therefore$三棱锥$V - AEF$外接球的体积为$\frac{4}{3}\pi×2^{3}=\frac{32\pi}{3}$。]
2. (2025·吉林长春八中高一下期中)三棱锥$P - ABC$中,平面$PAB\perp$平面$ABC,\triangle ABC$是边长为2的正三角形,$PA = PB = \sqrt{3}$,则三棱锥$P - ABC$外接球的表面积为 (
A.$\frac{35\pi}{3}$
B.$\frac{35\pi}{6}$
C.$\frac{35\pi}{12}$
D.$\frac{35\pi}{24}$
B
)A.$\frac{35\pi}{3}$
B.$\frac{35\pi}{6}$
C.$\frac{35\pi}{12}$
D.$\frac{35\pi}{24}$
答案:
2.B[提示:三棱锥$P - ABC$中,平面$PAB\perp$平面$ABC$,$\triangle ABC$是边长为$2$的正三角形,$PA = PB = \sqrt{3}$,如图所示, 取$AB$的中点$D$,连接$PD$,$\triangle ABC$的中心$E$,$\triangle PAB$的外心$F$,连接$AF$,作矩形$DEOF$,则点$O$为三棱锥$P - ABC$的外接球的球心,设$PF = r$,利用勾股定理,得$r^{2}=1^{2}+(\sqrt{2}-r)^{2}$,解得$r = \frac{3\sqrt{2}}{4}$,所以$DF=\sqrt{2}-\frac{3\sqrt{2}}{4}=\frac{\sqrt{2}}{4}$,所以外接球半径$R = AO = \sqrt{(\frac{2}{3}\sqrt{2^{2}-1^{2}})^{2}+(\frac{\sqrt{2}}{4})^{2}}=\sqrt{\frac{35}{24}}$,故$S_{球}=4\pi×(\sqrt{\frac{35}{24}})^{2}=\frac{35\pi}{6}$。]
取$AB$的中点$D$,连接$PD$,$\triangle ABC$的中心$E$,$\triangle PAB$的外心$F$,连接$AF$,作矩形$DEOF$,则点$O$为三棱锥$P - ABC$的外接球的球心,设$PF = r$,利用勾股定理,得$r^{2}=1^{2}+(\sqrt{2}-r)^{2}$,解得$r = \frac{3\sqrt{2}}{4}$,所以$DF=\sqrt{2}-\frac{3\sqrt{2}}{4}=\frac{\sqrt{2}}{4}$,所以外接球半径$R = AO = \sqrt{(\frac{2}{3}\sqrt{2^{2}-1^{2}})^{2}+(\frac{\sqrt{2}}{4})^{2}}=\sqrt{\frac{35}{24}}$,故$S_{球}=4\pi×(\sqrt{\frac{35}{24}})^{2}=\frac{35\pi}{6}$。]
2.B[提示:三棱锥$P - ABC$中,平面$PAB\perp$平面$ABC$,$\triangle ABC$是边长为$2$的正三角形,$PA = PB = \sqrt{3}$,如图所示,
 取$AB$的中点$D$,连接$PD$,$\triangle ABC$的中心$E$,$\triangle PAB$的外心$F$,连接$AF$,作矩形$DEOF$,则点$O$为三棱锥$P - ABC$的外接球的球心,设$PF = r$,利用勾股定理,得$r^{2}=1^{2}+(\sqrt{2}-r)^{2}$,解得$r = \frac{3\sqrt{2}}{4}$,所以$DF=\sqrt{2}-\frac{3\sqrt{2}}{4}=\frac{\sqrt{2}}{4}$,所以外接球半径$R = AO = \sqrt{(\frac{2}{3}\sqrt{2^{2}-1^{2}})^{2}+(\frac{\sqrt{2}}{4})^{2}}=\sqrt{\frac{35}{24}}$,故$S_{球}=4\pi×(\sqrt{\frac{35}{24}})^{2}=\frac{35\pi}{6}$。]
取$AB$的中点$D$,连接$PD$,$\triangle ABC$的中心$E$,$\triangle PAB$的外心$F$,连接$AF$,作矩形$DEOF$,则点$O$为三棱锥$P - ABC$的外接球的球心,设$PF = r$,利用勾股定理,得$r^{2}=1^{2}+(\sqrt{2}-r)^{2}$,解得$r = \frac{3\sqrt{2}}{4}$,所以$DF=\sqrt{2}-\frac{3\sqrt{2}}{4}=\frac{\sqrt{2}}{4}$,所以外接球半径$R = AO = \sqrt{(\frac{2}{3}\sqrt{2^{2}-1^{2}})^{2}+(\frac{\sqrt{2}}{4})^{2}}=\sqrt{\frac{35}{24}}$,故$S_{球}=4\pi×(\sqrt{\frac{35}{24}})^{2}=\frac{35\pi}{6}$。] 3. (2025·安徽师大学附中高一下期中)若三棱台$ABC - A_{1}B_{1}C_{1}$的上、下底面均是正三角形,侧面是全等的等腰梯形,且其各顶点都在表面积为$260\pi$的球$O$的表面上,$AB = 2A_{1}B_{1} = 8\sqrt{3}$,则三棱台$ABC - A_{1}B_{1}C_{1}$的高为 (
A.$2\sqrt{3}$
B.8
C.6或8
D.$2\sqrt{3}$或6
C
)A.$2\sqrt{3}$
B.8
C.6或8
D.$2\sqrt{3}$或6
答案:
3.C[提示:设点$O_{1}$,$O_{2}$分别是正三角形$A_{1}B_{1}C_{1}$,正三角形$ABC$的中心,球的半径为$R$,则$4\pi R^{2}=260\pi$,即$R^{2}=65$,且$O_{1}$,$O_{2}$,$O$三点共线,正三棱台$ABC - A_{1}B_{1}C_{1}$的高为$O_{1}O_{2}$,在等边三角形$ABC$中,$AB = 8\sqrt{3}$,由正弦定理可得$2AO_{2}=\frac{AB}{\sin60^{\circ}}=\frac{8\sqrt{3}}{\frac{\sqrt{3}}{2}}$,得$AO_{2}=8$,在等边三角形$A_{1}B_{1}C_{1}$中,$A_{1}B_{1}=4\sqrt{3}$,由正弦定理可得$2A_{1}O_{1}=\frac{A_{1}B_{1}}{\sin60^{\circ}}=\frac{4\sqrt{3}}{\frac{\sqrt{3}}{2}}$,得$A_{1}O_{1}=4$,在$Rt\triangle OO_{1}A_{1}$中,$OO_{1}^{2}+O_{1}A_{1}^{2}=R^{2}$,即$OO_{1}^{2}+16=65$,得$OO_{1}=7$,在$Rt\triangle OO_{2}A$中,$OO_{2}^{2}+O_{2}A^{2}=R^{2}$,即$OO_{2}^{2}+64=65$,得$OO_{2}=1$,如果三棱台的上下底面在球心$O$的两侧,如图
(2),那么正三棱台的高为$O_{1}O_{2}=OO_{1}+OO_{2}=7 + 1 = 8$,如果三棱台的上下底面在球心$O$的同侧,如图
(1)所示,那么正三棱台的高为$O_{1}O_{2}=OO_{1}-OO_{2}=7 - 1 = 6$,所以正三棱台$ABC - A_{1}B_{1}C_{1}$的高为$8$或$6$。]

3.C[提示:设点$O_{1}$,$O_{2}$分别是正三角形$A_{1}B_{1}C_{1}$,正三角形$ABC$的中心,球的半径为$R$,则$4\pi R^{2}=260\pi$,即$R^{2}=65$,且$O_{1}$,$O_{2}$,$O$三点共线,正三棱台$ABC - A_{1}B_{1}C_{1}$的高为$O_{1}O_{2}$,在等边三角形$ABC$中,$AB = 8\sqrt{3}$,由正弦定理可得$2AO_{2}=\frac{AB}{\sin60^{\circ}}=\frac{8\sqrt{3}}{\frac{\sqrt{3}}{2}}$,得$AO_{2}=8$,在等边三角形$A_{1}B_{1}C_{1}$中,$A_{1}B_{1}=4\sqrt{3}$,由正弦定理可得$2A_{1}O_{1}=\frac{A_{1}B_{1}}{\sin60^{\circ}}=\frac{4\sqrt{3}}{\frac{\sqrt{3}}{2}}$,得$A_{1}O_{1}=4$,在$Rt\triangle OO_{1}A_{1}$中,$OO_{1}^{2}+O_{1}A_{1}^{2}=R^{2}$,即$OO_{1}^{2}+16=65$,得$OO_{1}=7$,在$Rt\triangle OO_{2}A$中,$OO_{2}^{2}+O_{2}A^{2}=R^{2}$,即$OO_{2}^{2}+64=65$,得$OO_{2}=1$,如果三棱台的上下底面在球心$O$的两侧,如图
(2),那么正三棱台的高为$O_{1}O_{2}=OO_{1}+OO_{2}=7 + 1 = 8$,如果三棱台的上下底面在球心$O$的同侧,如图
(1)所示,那么正三棱台的高为$O_{1}O_{2}=OO_{1}-OO_{2}=7 - 1 = 6$,所以正三棱台$ABC - A_{1}B_{1}C_{1}$的高为$8$或$6$。]


4. (2025·吉林松原宁江区高一下期中)已知圆台的上、下底面的半径分别为1和3,球$O$与该圆台的上、下底面及其侧面都相切,则球$O$的体积为 (
A.$4\sqrt{3}\pi$
B.$12\pi$
C.$48\pi$
D.$32\sqrt{3}\pi$
A
)A.$4\sqrt{3}\pi$
B.$12\pi$
C.$48\pi$
D.$32\sqrt{3}\pi$
答案:
4.A[提示:设圆台的高为$h$,球$O$的半径为$R$,作出圆台的轴截面,如图所示, 已知圆台的上、下底面半径分别为$r = 1$,$R_{0}=3$,圆台的轴截面等腰梯形的高$h$等于球的直径$2R$,因为球与圆台侧面相切,所以$OE\perp AD$,所以$\triangle DOE\cong\triangle DOO_{1}$,$\triangle AOE\cong\triangle AOO_{1}$,所以$ED = O_{2}D$,$AE = AO_{1}$,所以母线$l = AE + ED = AO_{1}+DO_{2}=r + R_{0}=3 + 1 = 4$,同时$h = 2R$,由勾股定理可得$h^{2}+(R_{0}-r)^{2}=l^{2}$,将$l = 4$,$R_{0}-r = 3 - 1 = 2$,$h = 2R$,代入$h^{2}+(R_{0}-r)^{2}=l^{2}$中,得到$(2R)^{2}+2^{2}=4^{2}$,化简得$4R^{2}+4 = 16$,所以$R = \sqrt{3}$,则球$O$的体积为$\frac{4}{3}\pi×(\sqrt{3})^{3}=4\sqrt{3}\pi$。]
已知圆台的上、下底面半径分别为$r = 1$,$R_{0}=3$,圆台的轴截面等腰梯形的高$h$等于球的直径$2R$,因为球与圆台侧面相切,所以$OE\perp AD$,所以$\triangle DOE\cong\triangle DOO_{1}$,$\triangle AOE\cong\triangle AOO_{1}$,所以$ED = O_{2}D$,$AE = AO_{1}$,所以母线$l = AE + ED = AO_{1}+DO_{2}=r + R_{0}=3 + 1 = 4$,同时$h = 2R$,由勾股定理可得$h^{2}+(R_{0}-r)^{2}=l^{2}$,将$l = 4$,$R_{0}-r = 3 - 1 = 2$,$h = 2R$,代入$h^{2}+(R_{0}-r)^{2}=l^{2}$中,得到$(2R)^{2}+2^{2}=4^{2}$,化简得$4R^{2}+4 = 16$,所以$R = \sqrt{3}$,则球$O$的体积为$\frac{4}{3}\pi×(\sqrt{3})^{3}=4\sqrt{3}\pi$。]
4.A[提示:设圆台的高为$h$,球$O$的半径为$R$,作出圆台的轴截面,如图所示,
 已知圆台的上、下底面半径分别为$r = 1$,$R_{0}=3$,圆台的轴截面等腰梯形的高$h$等于球的直径$2R$,因为球与圆台侧面相切,所以$OE\perp AD$,所以$\triangle DOE\cong\triangle DOO_{1}$,$\triangle AOE\cong\triangle AOO_{1}$,所以$ED = O_{2}D$,$AE = AO_{1}$,所以母线$l = AE + ED = AO_{1}+DO_{2}=r + R_{0}=3 + 1 = 4$,同时$h = 2R$,由勾股定理可得$h^{2}+(R_{0}-r)^{2}=l^{2}$,将$l = 4$,$R_{0}-r = 3 - 1 = 2$,$h = 2R$,代入$h^{2}+(R_{0}-r)^{2}=l^{2}$中,得到$(2R)^{2}+2^{2}=4^{2}$,化简得$4R^{2}+4 = 16$,所以$R = \sqrt{3}$,则球$O$的体积为$\frac{4}{3}\pi×(\sqrt{3})^{3}=4\sqrt{3}\pi$。]
已知圆台的上、下底面半径分别为$r = 1$,$R_{0}=3$,圆台的轴截面等腰梯形的高$h$等于球的直径$2R$,因为球与圆台侧面相切,所以$OE\perp AD$,所以$\triangle DOE\cong\triangle DOO_{1}$,$\triangle AOE\cong\triangle AOO_{1}$,所以$ED = O_{2}D$,$AE = AO_{1}$,所以母线$l = AE + ED = AO_{1}+DO_{2}=r + R_{0}=3 + 1 = 4$,同时$h = 2R$,由勾股定理可得$h^{2}+(R_{0}-r)^{2}=l^{2}$,将$l = 4$,$R_{0}-r = 3 - 1 = 2$,$h = 2R$,代入$h^{2}+(R_{0}-r)^{2}=l^{2}$中,得到$(2R)^{2}+2^{2}=4^{2}$,化简得$4R^{2}+4 = 16$,所以$R = \sqrt{3}$,则球$O$的体积为$\frac{4}{3}\pi×(\sqrt{3})^{3}=4\sqrt{3}\pi$。] 5. [多选]数学中有许多形状优美、寓意独特的几何体,“勒洛四面体”就是其中之一.勒洛四面体是以正四面体的四个顶点为球心,以正四面体的棱长为半径的四个球的公共部分.如图所示,在勒洛四面体中,正四面体$A - BCD$的棱长为4,则下列结论正确的是 (
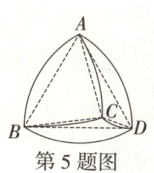
A.勒洛四面体最大的截面是正三角形
B.若$P,Q$是勒洛四面体$A - BCD$表面上的任意两点,则$PQ$的最大值为4
C.勒洛四面体$A - BCD$的体积是$8\sqrt{6}\pi$
D.勒洛四面体$A - BCD$内切球的半径是$4 - \sqrt{6}$
BD
)
A.勒洛四面体最大的截面是正三角形
B.若$P,Q$是勒洛四面体$A - BCD$表面上的任意两点,则$PQ$的最大值为4
C.勒洛四面体$A - BCD$的体积是$8\sqrt{6}\pi$
D.勒洛四面体$A - BCD$内切球的半径是$4 - \sqrt{6}$
答案:
5.BD[提示:由勒洛四面体的定义可知勒洛四面体最大的截面即经过四面体$A - BCD$表面的截面,如图
(1)所示,故A不正确。根据勒洛四面体的性质,它能在两个平行平面间自由转动,并且始终保持与两平面都接触,所以勒洛四面体表面上任意两点间的距离的最大值即为内接正四面体的棱长,所以勒洛四面体表面上任意两点间的距离的最大值为$4$,故B正确。如图
(2)所示,由对称性可知勒洛四面体内切球的球心$O$是正四面体$A - BCD$外接球的球心,连接$BO$,并延长交勒洛四面体的曲面于点$E$,则$OE$就是勒洛四面体内切球的半径。如图
(3)所示,在正四面体$A - BCD$中,$M$为$\triangle BCD$的中心,$O$是正四面体$A - BCD$外接球的球心,连接$BM$,$BO$,$AM$,由正四面体的性质可知$O$在$AM$上。因为$AB = 4$,所以$BM=\frac{2}{3}×\sqrt{4^{2}-2^{2}}=\frac{4\sqrt{3}}{3}$,则$AM=\sqrt{4^{2}-(\frac{4\sqrt{3}}{3})^{2}}=\frac{4\sqrt{6}}{3}$。因为$BO^{2}=BM^{2}+OM^{2}=(AM - OM)^{2}$,所以$BO^{2}=(\frac{4\sqrt{3}}{3})^{2}+OM^{2}=(\frac{4\sqrt{6}}{3}-OM)^{2}$,解得$BO = \sqrt{6}$,则正四面体$A - BCD$外接球的体积是$\frac{4}{3}\pi R^{3}=\frac{4}{3}\pi×(\sqrt{6})^{3}=8\sqrt{6}\pi$。因为勒洛四面体的体积小于正四面体$A - BCD$外接球的体积,所以C错误。因为$BE = AB = 4$,所以$OE = 4-\sqrt{6}$,故D正确。]


5.BD[提示:由勒洛四面体的定义可知勒洛四面体最大的截面即经过四面体$A - BCD$表面的截面,如图
(1)所示,故A不正确。根据勒洛四面体的性质,它能在两个平行平面间自由转动,并且始终保持与两平面都接触,所以勒洛四面体表面上任意两点间的距离的最大值即为内接正四面体的棱长,所以勒洛四面体表面上任意两点间的距离的最大值为$4$,故B正确。如图
(2)所示,由对称性可知勒洛四面体内切球的球心$O$是正四面体$A - BCD$外接球的球心,连接$BO$,并延长交勒洛四面体的曲面于点$E$,则$OE$就是勒洛四面体内切球的半径。如图
(3)所示,在正四面体$A - BCD$中,$M$为$\triangle BCD$的中心,$O$是正四面体$A - BCD$外接球的球心,连接$BM$,$BO$,$AM$,由正四面体的性质可知$O$在$AM$上。因为$AB = 4$,所以$BM=\frac{2}{3}×\sqrt{4^{2}-2^{2}}=\frac{4\sqrt{3}}{3}$,则$AM=\sqrt{4^{2}-(\frac{4\sqrt{3}}{3})^{2}}=\frac{4\sqrt{6}}{3}$。因为$BO^{2}=BM^{2}+OM^{2}=(AM - OM)^{2}$,所以$BO^{2}=(\frac{4\sqrt{3}}{3})^{2}+OM^{2}=(\frac{4\sqrt{6}}{3}-OM)^{2}$,解得$BO = \sqrt{6}$,则正四面体$A - BCD$外接球的体积是$\frac{4}{3}\pi R^{3}=\frac{4}{3}\pi×(\sqrt{6})^{3}=8\sqrt{6}\pi$。因为勒洛四面体的体积小于正四面体$A - BCD$外接球的体积,所以C错误。因为$BE = AB = 4$,所以$OE = 4-\sqrt{6}$,故D正确。]



6. [多选]已知四面体$A - BCD$的一个平面展开图如图所示,其中四边形$AEFD$是边长为$2\sqrt{2}$的菱形,$B,C$分别为$AE,FD$的中点,$BD = 2\sqrt{2}$,则在该四面体中 (

A.$BE\perp CD$
B.$BE$与平面$DCE$所成角的余弦值为$\frac{\sqrt{15}}{15}$
C.四面体$A - BCD$的内切球半径为$\frac{\sqrt{105}}{30}$
D.四面体$A - BCD$的外接球表面积为$8\pi$
ABC
)
A.$BE\perp CD$
B.$BE$与平面$DCE$所成角的余弦值为$\frac{\sqrt{15}}{15}$
C.四面体$A - BCD$的内切球半径为$\frac{\sqrt{105}}{30}$
D.四面体$A - BCD$的外接球表面积为$8\pi$
答案:
6.ABC[提示:由题意得展开图拼成的几何体如图所示, $AB = CD = \sqrt{2}$,$AD = BD = BC = AC = 2\sqrt{2}$,取$AB$的中点$M$,$CD$的中点$N$,连接$MN$,取$MN$的中点$O$,连接$OA$,过$O$作$OH\perp CM$于$H$,则$OH$是内切球的半径,$OA$是外接球的半径,$\therefore AM = CN = \frac{1}{2}AB = \frac{\sqrt{2}}{2}$,$CM = AN = \sqrt{AC^{2}-CN^{2}}=\sqrt{(2\sqrt{2})^{2}-(\frac{\sqrt{2}}{2})^{2}}=\frac{\sqrt{30}}{2}$,$MN = \sqrt{CM^{2}-CN^{2}}=\sqrt{(\frac{\sqrt{30}}{2})^{2}-(\frac{\sqrt{2}}{2})^{2}}=\sqrt{7}$。对于A,$AN\perp CD$,$BN\perp CD$,$AN\cap BN = N$,$\therefore CD\perp$平面$ABN$,$\because BE\subset$平面$ABN$,$\therefore BE\perp CD$,故A正确;对于B,$\because CD\subset$平面$ACD$,$\therefore$平面$ABN\perp$平面$ACD$,$\therefore\angle BAN$是$BE$与平面$DCE$所成角,$\therefore\cos\angle BAN=\frac{AM}{AN}=\frac{\sqrt{2}}{2}×\frac{2}{\sqrt{30}}=\frac{\sqrt{15}}{15}$,故B正确;对于C,$OH=\frac{CN}{CM}×\frac{1}{2}MN=\frac{\sqrt{2}}{2}×\frac{2}{\sqrt{30}}×\frac{1}{2}\sqrt{7}=\frac{\sqrt{105}}{30}$,故C正确;对于D,$OA^{2}=AM^{2}+(\frac{1}{2}MN)^{2}=(\frac{\sqrt{2}}{2})^{2}+(\frac{\sqrt{7}}{2})^{2}=\frac{9}{4}$,$\therefore$四面体$A - BCD$的外接球表面积为$4\pi×\frac{9}{4}=9\pi$,故D错误。]
$AB = CD = \sqrt{2}$,$AD = BD = BC = AC = 2\sqrt{2}$,取$AB$的中点$M$,$CD$的中点$N$,连接$MN$,取$MN$的中点$O$,连接$OA$,过$O$作$OH\perp CM$于$H$,则$OH$是内切球的半径,$OA$是外接球的半径,$\therefore AM = CN = \frac{1}{2}AB = \frac{\sqrt{2}}{2}$,$CM = AN = \sqrt{AC^{2}-CN^{2}}=\sqrt{(2\sqrt{2})^{2}-(\frac{\sqrt{2}}{2})^{2}}=\frac{\sqrt{30}}{2}$,$MN = \sqrt{CM^{2}-CN^{2}}=\sqrt{(\frac{\sqrt{30}}{2})^{2}-(\frac{\sqrt{2}}{2})^{2}}=\sqrt{7}$。对于A,$AN\perp CD$,$BN\perp CD$,$AN\cap BN = N$,$\therefore CD\perp$平面$ABN$,$\because BE\subset$平面$ABN$,$\therefore BE\perp CD$,故A正确;对于B,$\because CD\subset$平面$ACD$,$\therefore$平面$ABN\perp$平面$ACD$,$\therefore\angle BAN$是$BE$与平面$DCE$所成角,$\therefore\cos\angle BAN=\frac{AM}{AN}=\frac{\sqrt{2}}{2}×\frac{2}{\sqrt{30}}=\frac{\sqrt{15}}{15}$,故B正确;对于C,$OH=\frac{CN}{CM}×\frac{1}{2}MN=\frac{\sqrt{2}}{2}×\frac{2}{\sqrt{30}}×\frac{1}{2}\sqrt{7}=\frac{\sqrt{105}}{30}$,故C正确;对于D,$OA^{2}=AM^{2}+(\frac{1}{2}MN)^{2}=(\frac{\sqrt{2}}{2})^{2}+(\frac{\sqrt{7}}{2})^{2}=\frac{9}{4}$,$\therefore$四面体$A - BCD$的外接球表面积为$4\pi×\frac{9}{4}=9\pi$,故D错误。]
6.ABC[提示:由题意得展开图拼成的几何体如图所示,
 $AB = CD = \sqrt{2}$,$AD = BD = BC = AC = 2\sqrt{2}$,取$AB$的中点$M$,$CD$的中点$N$,连接$MN$,取$MN$的中点$O$,连接$OA$,过$O$作$OH\perp CM$于$H$,则$OH$是内切球的半径,$OA$是外接球的半径,$\therefore AM = CN = \frac{1}{2}AB = \frac{\sqrt{2}}{2}$,$CM = AN = \sqrt{AC^{2}-CN^{2}}=\sqrt{(2\sqrt{2})^{2}-(\frac{\sqrt{2}}{2})^{2}}=\frac{\sqrt{30}}{2}$,$MN = \sqrt{CM^{2}-CN^{2}}=\sqrt{(\frac{\sqrt{30}}{2})^{2}-(\frac{\sqrt{2}}{2})^{2}}=\sqrt{7}$。对于A,$AN\perp CD$,$BN\perp CD$,$AN\cap BN = N$,$\therefore CD\perp$平面$ABN$,$\because BE\subset$平面$ABN$,$\therefore BE\perp CD$,故A正确;对于B,$\because CD\subset$平面$ACD$,$\therefore$平面$ABN\perp$平面$ACD$,$\therefore\angle BAN$是$BE$与平面$DCE$所成角,$\therefore\cos\angle BAN=\frac{AM}{AN}=\frac{\sqrt{2}}{2}×\frac{2}{\sqrt{30}}=\frac{\sqrt{15}}{15}$,故B正确;对于C,$OH=\frac{CN}{CM}×\frac{1}{2}MN=\frac{\sqrt{2}}{2}×\frac{2}{\sqrt{30}}×\frac{1}{2}\sqrt{7}=\frac{\sqrt{105}}{30}$,故C正确;对于D,$OA^{2}=AM^{2}+(\frac{1}{2}MN)^{2}=(\frac{\sqrt{2}}{2})^{2}+(\frac{\sqrt{7}}{2})^{2}=\frac{9}{4}$,$\therefore$四面体$A - BCD$的外接球表面积为$4\pi×\frac{9}{4}=9\pi$,故D错误。]
$AB = CD = \sqrt{2}$,$AD = BD = BC = AC = 2\sqrt{2}$,取$AB$的中点$M$,$CD$的中点$N$,连接$MN$,取$MN$的中点$O$,连接$OA$,过$O$作$OH\perp CM$于$H$,则$OH$是内切球的半径,$OA$是外接球的半径,$\therefore AM = CN = \frac{1}{2}AB = \frac{\sqrt{2}}{2}$,$CM = AN = \sqrt{AC^{2}-CN^{2}}=\sqrt{(2\sqrt{2})^{2}-(\frac{\sqrt{2}}{2})^{2}}=\frac{\sqrt{30}}{2}$,$MN = \sqrt{CM^{2}-CN^{2}}=\sqrt{(\frac{\sqrt{30}}{2})^{2}-(\frac{\sqrt{2}}{2})^{2}}=\sqrt{7}$。对于A,$AN\perp CD$,$BN\perp CD$,$AN\cap BN = N$,$\therefore CD\perp$平面$ABN$,$\because BE\subset$平面$ABN$,$\therefore BE\perp CD$,故A正确;对于B,$\because CD\subset$平面$ACD$,$\therefore$平面$ABN\perp$平面$ACD$,$\therefore\angle BAN$是$BE$与平面$DCE$所成角,$\therefore\cos\angle BAN=\frac{AM}{AN}=\frac{\sqrt{2}}{2}×\frac{2}{\sqrt{30}}=\frac{\sqrt{15}}{15}$,故B正确;对于C,$OH=\frac{CN}{CM}×\frac{1}{2}MN=\frac{\sqrt{2}}{2}×\frac{2}{\sqrt{30}}×\frac{1}{2}\sqrt{7}=\frac{\sqrt{105}}{30}$,故C正确;对于D,$OA^{2}=AM^{2}+(\frac{1}{2}MN)^{2}=(\frac{\sqrt{2}}{2})^{2}+(\frac{\sqrt{7}}{2})^{2}=\frac{9}{4}$,$\therefore$四面体$A - BCD$的外接球表面积为$4\pi×\frac{9}{4}=9\pi$,故D错误。] 7. (2025·浙江杭州高一下期末)[多选] 在棱长为3的正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$中,$M$为$DD_{1}$的中点,$F$为侧面$AA_{1}D_{1}D$内一动点,满足$B_{1}F//$平面$BC_{1}M$,则 (
A.三棱锥$A - A_{1}BC$的外接球表面积为$27\pi$
B.三棱锥$F - BC_{1}M$的体积是定值
C.动点$F$的轨迹是一条圆弧,长度为$\frac{9\pi}{16}$
D.动点$F$的轨迹是一条线段,长度为$\frac{3\sqrt{2}}{2}$
ABD
)A.三棱锥$A - A_{1}BC$的外接球表面积为$27\pi$
B.三棱锥$F - BC_{1}M$的体积是定值
C.动点$F$的轨迹是一条圆弧,长度为$\frac{9\pi}{16}$
D.动点$F$的轨迹是一条线段,长度为$\frac{3\sqrt{2}}{2}$
答案:
7.ABD[提示:对于A,由题意可知三棱锥$A - A_{1}BC$的外接球即为正方体的外接球,可知正方体外接球的直径为正方体的体对角线,设正方体外接球的半径为$R$,则$2R=\sqrt{3^{2}+3^{2}+3^{2}}=3\sqrt{3}$,即$R = \frac{3\sqrt{3}}{2}$,所以三棱锥$A - A_{1}BC$的外接球表面积为$4\pi R^{2}=4\pi×(\frac{3\sqrt{3}}{2})^{2}=27\pi$,故A正确;对于B,因为$B_{1}F//$平面$BC_{1}M$,所以$F$点到平面$BC_{1}M$的距离为定值,又$\triangle BC_{1}M$的面积为定值,所以三棱锥$F - BC_{1}M$的体积为定值,故B正确;对于C,取$AA_{1}$,$A_{1}D_{1}$的中点$H$,$N$,连接$HB_{1}$,$NB_{1}$,$HN$,$HM$,如图所示, 因为$HM// B_{1}C_{1}$且$HM = B_{1}C_{1}$,所以四边形$HMC_{1}B_{1}$为平行四边形,所以$HB_{1}// MC_{1}$,同理可得$AD_{1}// BC_{1}$,又因为$HN// AD_{1}$,所以$HN// BC_{1}$,又因为$HB_{1}\subset$平面$HNB_{1}$,$HN\subset$平面$HNB_{1}$,$HB_{1}\cap HN = H$,$MC_{1}\subset$平面$BMC_{1}$,$BC_{1}\subset$平面$BMC_{1}$且$MC_{1}\cap BC_{1}=C_{1}$,所以平面$HNB_{1}//$平面$BMC_{1}$,又$B_{1}F\subset$平面$BC_{1}M$,所以$F$点的轨迹为线段$HN$;对于D,由选项C可知$F$点的轨迹为线段$HN$,$HN=\frac{1}{2}AD_{1}=\frac{1}{2}\sqrt{3^{2}+3^{2}}=\frac{3\sqrt{2}}{2}$,故D正确。]
因为$HM// B_{1}C_{1}$且$HM = B_{1}C_{1}$,所以四边形$HMC_{1}B_{1}$为平行四边形,所以$HB_{1}// MC_{1}$,同理可得$AD_{1}// BC_{1}$,又因为$HN// AD_{1}$,所以$HN// BC_{1}$,又因为$HB_{1}\subset$平面$HNB_{1}$,$HN\subset$平面$HNB_{1}$,$HB_{1}\cap HN = H$,$MC_{1}\subset$平面$BMC_{1}$,$BC_{1}\subset$平面$BMC_{1}$且$MC_{1}\cap BC_{1}=C_{1}$,所以平面$HNB_{1}//$平面$BMC_{1}$,又$B_{1}F\subset$平面$BC_{1}M$,所以$F$点的轨迹为线段$HN$;对于D,由选项C可知$F$点的轨迹为线段$HN$,$HN=\frac{1}{2}AD_{1}=\frac{1}{2}\sqrt{3^{2}+3^{2}}=\frac{3\sqrt{2}}{2}$,故D正确。]
7.ABD[提示:对于A,由题意可知三棱锥$A - A_{1}BC$的外接球即为正方体的外接球,可知正方体外接球的直径为正方体的体对角线,设正方体外接球的半径为$R$,则$2R=\sqrt{3^{2}+3^{2}+3^{2}}=3\sqrt{3}$,即$R = \frac{3\sqrt{3}}{2}$,所以三棱锥$A - A_{1}BC$的外接球表面积为$4\pi R^{2}=4\pi×(\frac{3\sqrt{3}}{2})^{2}=27\pi$,故A正确;对于B,因为$B_{1}F//$平面$BC_{1}M$,所以$F$点到平面$BC_{1}M$的距离为定值,又$\triangle BC_{1}M$的面积为定值,所以三棱锥$F - BC_{1}M$的体积为定值,故B正确;对于C,取$AA_{1}$,$A_{1}D_{1}$的中点$H$,$N$,连接$HB_{1}$,$NB_{1}$,$HN$,$HM$,如图所示,
 因为$HM// B_{1}C_{1}$且$HM = B_{1}C_{1}$,所以四边形$HMC_{1}B_{1}$为平行四边形,所以$HB_{1}// MC_{1}$,同理可得$AD_{1}// BC_{1}$,又因为$HN// AD_{1}$,所以$HN// BC_{1}$,又因为$HB_{1}\subset$平面$HNB_{1}$,$HN\subset$平面$HNB_{1}$,$HB_{1}\cap HN = H$,$MC_{1}\subset$平面$BMC_{1}$,$BC_{1}\subset$平面$BMC_{1}$且$MC_{1}\cap BC_{1}=C_{1}$,所以平面$HNB_{1}//$平面$BMC_{1}$,又$B_{1}F\subset$平面$BC_{1}M$,所以$F$点的轨迹为线段$HN$;对于D,由选项C可知$F$点的轨迹为线段$HN$,$HN=\frac{1}{2}AD_{1}=\frac{1}{2}\sqrt{3^{2}+3^{2}}=\frac{3\sqrt{2}}{2}$,故D正确。]
因为$HM// B_{1}C_{1}$且$HM = B_{1}C_{1}$,所以四边形$HMC_{1}B_{1}$为平行四边形,所以$HB_{1}// MC_{1}$,同理可得$AD_{1}// BC_{1}$,又因为$HN// AD_{1}$,所以$HN// BC_{1}$,又因为$HB_{1}\subset$平面$HNB_{1}$,$HN\subset$平面$HNB_{1}$,$HB_{1}\cap HN = H$,$MC_{1}\subset$平面$BMC_{1}$,$BC_{1}\subset$平面$BMC_{1}$且$MC_{1}\cap BC_{1}=C_{1}$,所以平面$HNB_{1}//$平面$BMC_{1}$,又$B_{1}F\subset$平面$BC_{1}M$,所以$F$点的轨迹为线段$HN$;对于D,由选项C可知$F$点的轨迹为线段$HN$,$HN=\frac{1}{2}AD_{1}=\frac{1}{2}\sqrt{3^{2}+3^{2}}=\frac{3\sqrt{2}}{2}$,故D正确。] 查看更多完整答案,请扫码查看


