2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年零失误分层训练高中数学必修第二册人教版黑吉辽内蒙古专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
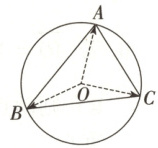
2. 已知$\triangle ABC$内接于$\odot O$,$AB = c,BC = a,CA = b$,$\odot O$的半径为$r$.
(1)若$\overrightarrow{OA}+2\overrightarrow{OB}+\sqrt{3}\overrightarrow{OC}=\boldsymbol{0}$,试求$\angle BOC$的大小;
(2)若$A$为动点,$\angle BAC = 60°$,$\overrightarrow{AO}=\lambda\overrightarrow{OC}+\mu\overrightarrow{OB}$,试求$\lambda +\mu$的最大值.
(1)若$\overrightarrow{OA}+2\overrightarrow{OB}+\sqrt{3}\overrightarrow{OC}=\boldsymbol{0}$,试求$\angle BOC$的大小;
(2)若$A$为动点,$\angle BAC = 60°$,$\overrightarrow{AO}=\lambda\overrightarrow{OC}+\mu\overrightarrow{OB}$,试求$\lambda +\mu$的最大值.

答案:
2.
(1)解:
∵$\overrightarrow{OA}+2\overrightarrow{OB}+\sqrt{3}\overrightarrow{OC}=\overrightarrow{0}$,
∴$\overrightarrow{AO}=2\overrightarrow{OB}+\sqrt{3}\overrightarrow{OC}$,
∴$\overrightarrow{AO}^2=(2\overrightarrow{OB}+\sqrt{3}\overrightarrow{OC})^2$.
∵$\overrightarrow{AO}=\overrightarrow{OB}=\overrightarrow{OC}=r$,
∴$r^2 = 4r^2 + 2×2×\sqrt{3}r^2×\cos\angle BOC + 3r^2$,
解得$\cos\angle BOC=-\frac{\sqrt{3}}{2}$,
由题意得$\angle BOC\in(0, \pi)$,
∴$\angle BOC=\frac{5\pi}{6}$.
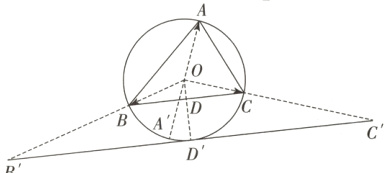
(2)解法1(等和线):过点O作OD'⊥BC交BC于D,交⊙O于D',连接BD',CD',过点D作B'C'//BC,交OB的延长线于B',交OC的延长线于C',延长AO交⊙O于A'.
∵$\overrightarrow{AO}=\lambda\overrightarrow{OC}+\mu\overrightarrow{OB}$,且$\overrightarrow{AO}=\overrightarrow{OA'}$,
∴$\overrightarrow{OA'}=\lambda\overrightarrow{OC}+\mu\overrightarrow{OB}$.
∵OD'⊥BC交BC于D,交⊙O于D',且过点D的直线B'C'//BC,
∴直线B'C'与⊙O相切于点D'.
∵OD'⊥BC交BC于D,
∴OD垂直平分线段BC.
∵$\angle BAC = 60^{\circ}$,
∴$\angle BOC = 2\angle BAC = 120^{\circ}$.
∵$\overrightarrow{OB}=\overrightarrow{OC}$,OD垂直平分线段BC,
∴OD平分$\angle BOC$,
∴$\angle BOD=\frac{\angle BOC}{2}=60^{\circ}$,
∴$OD = \overrightarrow{OB}\cos\angle BOD=\frac{1}{2}\overrightarrow{OB}=\frac{1}{2}OD'$.
∵当A'与D'重合时,$\lambda + \mu = k$取得最大值,$k_{max}=\frac{\overrightarrow{OB'}}{\overrightarrow{OB}}=\frac{\overrightarrow{OD'}}{\overrightarrow{OD}} = 2$,
∴$\lambda + \mu$的最大值为2.
解法2:
∵⊙O中,$\angle BAC = 60^{\circ}$,
∴$\angle BOC = 120^{\circ}$.
∵$\overrightarrow{AO}=\lambda\overrightarrow{OC}+\mu\overrightarrow{OB}$,
∴$\overrightarrow{AO}^2=(\lambda\overrightarrow{OC}+\mu\overrightarrow{OB})^2$,
∴$r^2=\lambda^2r^2 + 2×\lambda×\mu r^2×\cos120^{\circ}+\mu^2r^2$,
∴$\lambda^2+\mu^2=\lambda\mu + 1$.
根据题意,可知$\lambda>0$,$\mu>0$,
∴$(\lambda + \mu)^2 = 3\lambda\mu + 1\leqslant3×\frac{(\lambda + \mu)^2}{4}+1$(当且仅当$\lambda = \mu$时等号成立),
∴$(\lambda + \mu)^2\leqslant4$,
∴$\lambda + \mu\leqslant2$,
∴$\lambda + \mu$的最大值为2.
2.
(1)解:
∵$\overrightarrow{OA}+2\overrightarrow{OB}+\sqrt{3}\overrightarrow{OC}=\overrightarrow{0}$,
∴$\overrightarrow{AO}=2\overrightarrow{OB}+\sqrt{3}\overrightarrow{OC}$,
∴$\overrightarrow{AO}^2=(2\overrightarrow{OB}+\sqrt{3}\overrightarrow{OC})^2$.
∵$\overrightarrow{AO}=\overrightarrow{OB}=\overrightarrow{OC}=r$,
∴$r^2 = 4r^2 + 2×2×\sqrt{3}r^2×\cos\angle BOC + 3r^2$,
解得$\cos\angle BOC=-\frac{\sqrt{3}}{2}$,
由题意得$\angle BOC\in(0, \pi)$,
∴$\angle BOC=\frac{5\pi}{6}$.
(2)解法1(等和线):过点O作OD'⊥BC交BC于D,交⊙O于D',连接BD',CD',过点D作B'C'//BC,交OB的延长线于B',交OC的延长线于C',延长AO交⊙O于A'.
∵$\overrightarrow{AO}=\lambda\overrightarrow{OC}+\mu\overrightarrow{OB}$,且$\overrightarrow{AO}=\overrightarrow{OA'}$,
∴$\overrightarrow{OA'}=\lambda\overrightarrow{OC}+\mu\overrightarrow{OB}$.
∵OD'⊥BC交BC于D,交⊙O于D',且过点D的直线B'C'//BC,
∴直线B'C'与⊙O相切于点D'.
∵OD'⊥BC交BC于D,
∴OD垂直平分线段BC.
∵$\angle BAC = 60^{\circ}$,
∴$\angle BOC = 2\angle BAC = 120^{\circ}$.
∵$\overrightarrow{OB}=\overrightarrow{OC}$,OD垂直平分线段BC,

∴OD平分$\angle BOC$,
∴$\angle BOD=\frac{\angle BOC}{2}=60^{\circ}$,
∴$OD = \overrightarrow{OB}\cos\angle BOD=\frac{1}{2}\overrightarrow{OB}=\frac{1}{2}OD'$.
∵当A'与D'重合时,$\lambda + \mu = k$取得最大值,$k_{max}=\frac{\overrightarrow{OB'}}{\overrightarrow{OB}}=\frac{\overrightarrow{OD'}}{\overrightarrow{OD}} = 2$,
∴$\lambda + \mu$的最大值为2.
解法2:
∵⊙O中,$\angle BAC = 60^{\circ}$,
∴$\angle BOC = 120^{\circ}$.
∵$\overrightarrow{AO}=\lambda\overrightarrow{OC}+\mu\overrightarrow{OB}$,
∴$\overrightarrow{AO}^2=(\lambda\overrightarrow{OC}+\mu\overrightarrow{OB})^2$,
∴$r^2=\lambda^2r^2 + 2×\lambda×\mu r^2×\cos120^{\circ}+\mu^2r^2$,
∴$\lambda^2+\mu^2=\lambda\mu + 1$.
根据题意,可知$\lambda>0$,$\mu>0$,
∴$(\lambda + \mu)^2 = 3\lambda\mu + 1\leqslant3×\frac{(\lambda + \mu)^2}{4}+1$(当且仅当$\lambda = \mu$时等号成立),
∴$(\lambda + \mu)^2\leqslant4$,
∴$\lambda + \mu\leqslant2$,
∴$\lambda + \mu$的最大值为2.
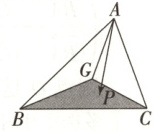
3. 已知点$G$是$\triangle ABC$的重心,点$P$是$\triangle GBC$内一点(不包括边界),设$\overrightarrow{AB}=\boldsymbol{a},\overrightarrow{AC}=\boldsymbol{b}$.
(1)试用$\boldsymbol{a},\boldsymbol{b}$表示$\overrightarrow{AG}$;
(2)若$\overrightarrow{AP}=\lambda\boldsymbol{a}+\mu\boldsymbol{b}$,求$\lambda +\mu$的取值范围.
(1)试用$\boldsymbol{a},\boldsymbol{b}$表示$\overrightarrow{AG}$;
(2)若$\overrightarrow{AP}=\lambda\boldsymbol{a}+\mu\boldsymbol{b}$,求$\lambda +\mu$的取值范围.

答案:
3.
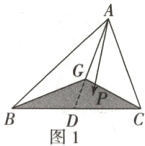
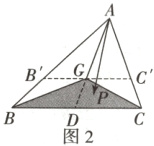
(1)解:如图1,延长AG,交BC于点D,则D为BC的中点,
$\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AD}=\frac{2}{3}(\overrightarrow{AB}+\overrightarrow{BD})=\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{BC}=\frac{2}{3}\left[\overrightarrow{AB}+\frac{1}{2}(\overrightarrow{AC}-\overrightarrow{AB})\right]=\frac{1}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}$.
(2)解法1(等和线):过点G作B'C'//BC交AB于B',交AC于C',如图2所示.
∵$\overrightarrow{AP}=\lambda\overrightarrow{a}+\mu\overrightarrow{b}$,且点P是△GBC内一点(不包括边界),
∴$\frac{2}{3}=\frac{\overrightarrow{AG}}{\overrightarrow{AD}}=\frac{\overrightarrow{AB'}}{\overrightarrow{AB}}<\lambda + \mu = k<\frac{\overrightarrow{AB}}{\overrightarrow{AB}} = 1$,
即$\lambda + \mu\in(\frac{2}{3},1)$.
解法2:$\overrightarrow{GB}=\overrightarrow{AB}-\overrightarrow{AG}=\frac{2}{3}\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}$,连接GP并延长,交BC于点P',如图3所示,
又$\overrightarrow{AP}=\overrightarrow{AG}+\overrightarrow{GP'}=\frac{1}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}+t(\overrightarrow{GB}+\overrightarrow{BP'})=\frac{1}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}+t\left(\frac{2}{3}\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+m(\overrightarrow{b}-\overrightarrow{a})\right)=\left(\frac{1}{3}+\frac{2}{3}t-tm\right)\overrightarrow{a}+\left(\frac{1}{3}+\frac{1}{3}t+tm\right)\overrightarrow{b}$(其中0 < t < 1,0 < m < 1).
因为$\overrightarrow{AP}=\lambda\overrightarrow{a}+\mu\overrightarrow{b}$,所以$\lambda=\frac{1}{3}+\frac{2}{3}t-tm$,$\mu=\frac{1}{3}+\frac{1}{3}t+tm$,
故$\lambda + \mu=\frac{2}{3}+\frac{1}{3}t$,
因为0 < t < 1,所以$\lambda + \mu=\frac{2}{3}+\frac{1}{3}t\in(\frac{2}{3},1)$.

3.
(1)解:如图1,延长AG,交BC于点D,则D为BC的中点,
$\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AD}=\frac{2}{3}(\overrightarrow{AB}+\overrightarrow{BD})=\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{BC}=\frac{2}{3}\left[\overrightarrow{AB}+\frac{1}{2}(\overrightarrow{AC}-\overrightarrow{AB})\right]=\frac{1}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}$.

(2)解法1(等和线):过点G作B'C'//BC交AB于B',交AC于C',如图2所示.
∵$\overrightarrow{AP}=\lambda\overrightarrow{a}+\mu\overrightarrow{b}$,且点P是△GBC内一点(不包括边界),
∴$\frac{2}{3}=\frac{\overrightarrow{AG}}{\overrightarrow{AD}}=\frac{\overrightarrow{AB'}}{\overrightarrow{AB}}<\lambda + \mu = k<\frac{\overrightarrow{AB}}{\overrightarrow{AB}} = 1$,
即$\lambda + \mu\in(\frac{2}{3},1)$.
解法2:$\overrightarrow{GB}=\overrightarrow{AB}-\overrightarrow{AG}=\frac{2}{3}\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}$,连接GP并延长,交BC于点P',如图3所示,
又$\overrightarrow{AP}=\overrightarrow{AG}+\overrightarrow{GP'}=\frac{1}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}+t(\overrightarrow{GB}+\overrightarrow{BP'})=\frac{1}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}+t\left(\frac{2}{3}\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+m(\overrightarrow{b}-\overrightarrow{a})\right)=\left(\frac{1}{3}+\frac{2}{3}t-tm\right)\overrightarrow{a}+\left(\frac{1}{3}+\frac{1}{3}t+tm\right)\overrightarrow{b}$(其中0 < t < 1,0 < m < 1).
因为$\overrightarrow{AP}=\lambda\overrightarrow{a}+\mu\overrightarrow{b}$,所以$\lambda=\frac{1}{3}+\frac{2}{3}t-tm$,$\mu=\frac{1}{3}+\frac{1}{3}t+tm$,
故$\lambda + \mu=\frac{2}{3}+\frac{1}{3}t$,
因为0 < t < 1,所以$\lambda + \mu=\frac{2}{3}+\frac{1}{3}t\in(\frac{2}{3},1)$.


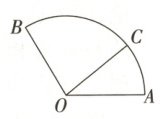
4.(2024·陕西西安交大附中高一下期中)在如图所示的扇形$AOB$中,扇形的半径为$2$,$\angle AOB = \frac{2\pi}{3}$,点$C$在弧$AB$上移动,$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$.
(1)若$\angle AOC=\frac{\pi}{6}$,求$x + y$的值;
(2)求$x + y$的最大值.
(1)若$\angle AOC=\frac{\pi}{6}$,求$x + y$的值;
(2)求$x + y$的最大值.

答案:
4.
(1)解法1(等和线):
如图1所示,连接AB,过点C作$A_1B_1 // AB$,交OA的延长线于点$A_1$,交OB的延长线于点$B_1$.
∵$OA = OB$,且$\angle AOB=\frac{2\pi}{3}$,
∴$\angle OBA=\angle OAB=\frac{\pi}{6}$.
∵$A_1B_1 // AB$,
∴$\angle A_1=\angle OAB=\frac{\pi}{6}$.
∵$\angle AOC=\frac{\pi}{6}$,
∴$\angle OCA=\frac{2\pi}{3}$,$A_1C = OC = 2$.
∴根据余弦定理可知$OA_1=\sqrt{CA_1^2 + OC^2 - 2CA_1· OC·\cos\angle OCA}=\sqrt{2^2 + 2^2 - 2×2×2×\cos\frac{2\pi}{3}} = 2\sqrt{3}$,
∴$x + y = k=\frac{OA_1}{OA}=\frac{2\sqrt{3}}{2}=\sqrt{3}$.
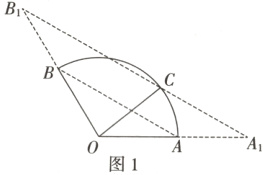
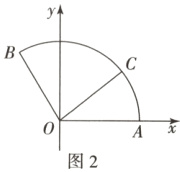
解法2:
如图2所示,以O为原点,以OA所在直线为x轴,以过O且与OA垂直的直线为y轴,建立平面直角坐标系,则$A(2, 0)$,$B(-1, \sqrt{3})$,
设$\angle AOC=\theta$,则$\theta\in\left[0, \frac{2\pi}{3}\right]$,所以$C(2\cos\theta, 2\sin\theta)$,$\overrightarrow{OC}=(2\cos\theta, 2\sin\theta)$.
当$\angle AOC=\frac{\pi}{6}$时,可得$C(\sqrt{3}, 1)$,
由$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$,可得$(\sqrt{3}, 1)=x(2, 0)+y(-1, \sqrt{3})$,
即$\begin{cases} \sqrt{3}=2x - y \\ 1=\sqrt{3}y \end{cases}$,
解得$\begin{cases} x=\frac{2\sqrt{3}}{3} \\ y=\frac{\sqrt{3}}{3} \end{cases}$,
所以$x + y=\sqrt{3}$.
(2)解法1:因为$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$,所以$\begin{cases} 2\cos\theta=2x - y \\ 2\sin\theta=\sqrt{3}y \end{cases}$,
所以$x + y=\sqrt{3}\sin\theta+\frac{2\sqrt{3}}{3}\cos\theta = 2\sin\left(\theta+\frac{\pi}{6}\right)$,
又$0\leqslant\theta\leqslant\frac{2\pi}{3}$,所以$\frac{\pi}{6}\leqslant\theta+\frac{\pi}{6}\leqslant\frac{5\pi}{6}$,
所以当$\theta=\frac{\pi}{3}$时,$x + y$取得最大值2,即$x + y$的最大值为2.
解法2:如图3所示,连接AB,过点O作$OD\perp AB$交弧AB于点D,过点D作$A_2B_2 // AB$,交OA的延长线于点$A_2$,交OB的延长线于点$B_2$,
易知当点C与D重合时,$x + y$取得最大值,
∵直线$A_2B_2 // AB$,$OD\perp AB$,
∴$\angle A_2=\angle OAB=\frac{\pi}{6}$,$\angle ODA_2=\frac{\pi}{2}$,
∴$(x + y)_{max}=k_{max}=\frac{OA_2}{OA}=\frac{OA_2}{OD\sin\frac{\pi}{6}} = 2$,即$x + y$的最大值为2.

4.
(1)解法1(等和线):
如图1所示,连接AB,过点C作$A_1B_1 // AB$,交OA的延长线于点$A_1$,交OB的延长线于点$B_1$.
∵$OA = OB$,且$\angle AOB=\frac{2\pi}{3}$,
∴$\angle OBA=\angle OAB=\frac{\pi}{6}$.
∵$A_1B_1 // AB$,
∴$\angle A_1=\angle OAB=\frac{\pi}{6}$.
∵$\angle AOC=\frac{\pi}{6}$,
∴$\angle OCA=\frac{2\pi}{3}$,$A_1C = OC = 2$.
∴根据余弦定理可知$OA_1=\sqrt{CA_1^2 + OC^2 - 2CA_1· OC·\cos\angle OCA}=\sqrt{2^2 + 2^2 - 2×2×2×\cos\frac{2\pi}{3}} = 2\sqrt{3}$,
∴$x + y = k=\frac{OA_1}{OA}=\frac{2\sqrt{3}}{2}=\sqrt{3}$.

解法2:
如图2所示,以O为原点,以OA所在直线为x轴,以过O且与OA垂直的直线为y轴,建立平面直角坐标系,则$A(2, 0)$,$B(-1, \sqrt{3})$,
设$\angle AOC=\theta$,则$\theta\in\left[0, \frac{2\pi}{3}\right]$,所以$C(2\cos\theta, 2\sin\theta)$,$\overrightarrow{OC}=(2\cos\theta, 2\sin\theta)$.
当$\angle AOC=\frac{\pi}{6}$时,可得$C(\sqrt{3}, 1)$,
由$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$,可得$(\sqrt{3}, 1)=x(2, 0)+y(-1, \sqrt{3})$,
即$\begin{cases} \sqrt{3}=2x - y \\ 1=\sqrt{3}y \end{cases}$,
解得$\begin{cases} x=\frac{2\sqrt{3}}{3} \\ y=\frac{\sqrt{3}}{3} \end{cases}$,
所以$x + y=\sqrt{3}$.

(2)解法1:因为$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$,所以$\begin{cases} 2\cos\theta=2x - y \\ 2\sin\theta=\sqrt{3}y \end{cases}$,
所以$x + y=\sqrt{3}\sin\theta+\frac{2\sqrt{3}}{3}\cos\theta = 2\sin\left(\theta+\frac{\pi}{6}\right)$,
又$0\leqslant\theta\leqslant\frac{2\pi}{3}$,所以$\frac{\pi}{6}\leqslant\theta+\frac{\pi}{6}\leqslant\frac{5\pi}{6}$,
所以当$\theta=\frac{\pi}{3}$时,$x + y$取得最大值2,即$x + y$的最大值为2.
解法2:如图3所示,连接AB,过点O作$OD\perp AB$交弧AB于点D,过点D作$A_2B_2 // AB$,交OA的延长线于点$A_2$,交OB的延长线于点$B_2$,
易知当点C与D重合时,$x + y$取得最大值,
∵直线$A_2B_2 // AB$,$OD\perp AB$,
∴$\angle A_2=\angle OAB=\frac{\pi}{6}$,$\angle ODA_2=\frac{\pi}{2}$,
∴$(x + y)_{max}=k_{max}=\frac{OA_2}{OA}=\frac{OA_2}{OD\sin\frac{\pi}{6}} = 2$,即$x + y$的最大值为2.

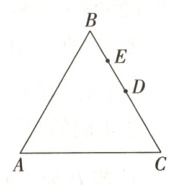
5.(2025·重庆一中高一下月考)如图,在边长为$8$的正三角形$ABC$中,$D$为$BC$的中点,$E$为$BD$的中
点.
(1)若点$P$为$\triangle ABC$的重心,且有$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AC}$,求$m$和$n$的值;
(2)若点$Q$在以点$E$为圆心、半径为$\sqrt{3}$的圆上运动,且有$\overrightarrow{AQ}=x\overrightarrow{AB}+y\overrightarrow{AC}$,求$x + y$的取值范围.
点.
(1)若点$P$为$\triangle ABC$的重心,且有$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AC}$,求$m$和$n$的值;
(2)若点$Q$在以点$E$为圆心、半径为$\sqrt{3}$的圆上运动,且有$\overrightarrow{AQ}=x\overrightarrow{AB}+y\overrightarrow{AC}$,求$x + y$的取值范围.

答案:
5.
(1)解:因为点P为△ABC的重心,所以$\overrightarrow{AP}=\frac{2}{3}\overrightarrow{AD}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})=m\overrightarrow{AB}+n\overrightarrow{AC}$,所以$m = n=\frac{1}{3}$.
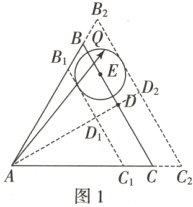
(2)解法1(等和线):作BC边的平行线$B_1C_1$和$B_2C_2$,分别与圆E相切,连接AD并延长交$B_1C_1$于$D_1$,交$B_2C_2$于$D_2$,如图1所示,
易知当Q位于$B_1C_1$与圆E的切点位置时,$x + y$取得最小值;当Q位于$B_2C_2$与圆E相切的位置时,$x + y$取得最大值.
即有$\frac{3}{4}=\frac{4\sqrt{3}-\sqrt{3}}{4\sqrt{3}}=\frac{AD - r}{AD}=\frac{\overrightarrow{AD_1}}{\overrightarrow{AD}}=\frac{\overrightarrow{AB_1}}{\overrightarrow{AB}}\leqslant x + y = k\leqslant\frac{\overrightarrow{AB_2}}{\overrightarrow{AB}}=\frac{\overrightarrow{AD_2}}{\overrightarrow{AD}}=\frac{AD + r}{AD}=\frac{4\sqrt{3}+\sqrt{3}}{4\sqrt{3}}=\frac{5}{4}$,
故$x + y\in\left[\frac{3}{4}, \frac{5}{4}\right]$.
解法2:以D为原点,DB,DA所在直线分别为x轴、y轴建立直角坐标系,如图2所示,则$C(-4, 0)$,$B(4, 0)$,$E(2, 0)$,$A(0, 4\sqrt{3})$.
因为点Q所在圆的方程为$(x - 2)^2 + y^2 = 3$,所以可设$Q(2+\sqrt{3}\cos\theta, \sqrt{3}\sin\theta)$,
所以$\overrightarrow{AC}=(-4, -4\sqrt{3})$,$\overrightarrow{AB}=(4, -4\sqrt{3})$,$\overrightarrow{AQ}=(2+\sqrt{3}\cos\theta, \sqrt{3}\sin\theta - 4\sqrt{3})$.
因为$\overrightarrow{AQ}=x\overrightarrow{AB}+y\overrightarrow{AC}$,所以$-4\sqrt{3}x - 4\sqrt{3}y=\sqrt{3}\sin\theta - 4\sqrt{3}$,即$x + y = 1-\frac{\sin\theta}{4}$.
所以由$\sin\theta\in[-1, 1]$,可得$x + y\in\left[\frac{3}{4}, \frac{5}{4}\right]$.

5.
(1)解:因为点P为△ABC的重心,所以$\overrightarrow{AP}=\frac{2}{3}\overrightarrow{AD}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})=m\overrightarrow{AB}+n\overrightarrow{AC}$,所以$m = n=\frac{1}{3}$.
(2)解法1(等和线):作BC边的平行线$B_1C_1$和$B_2C_2$,分别与圆E相切,连接AD并延长交$B_1C_1$于$D_1$,交$B_2C_2$于$D_2$,如图1所示,
易知当Q位于$B_1C_1$与圆E的切点位置时,$x + y$取得最小值;当Q位于$B_2C_2$与圆E相切的位置时,$x + y$取得最大值.
即有$\frac{3}{4}=\frac{4\sqrt{3}-\sqrt{3}}{4\sqrt{3}}=\frac{AD - r}{AD}=\frac{\overrightarrow{AD_1}}{\overrightarrow{AD}}=\frac{\overrightarrow{AB_1}}{\overrightarrow{AB}}\leqslant x + y = k\leqslant\frac{\overrightarrow{AB_2}}{\overrightarrow{AB}}=\frac{\overrightarrow{AD_2}}{\overrightarrow{AD}}=\frac{AD + r}{AD}=\frac{4\sqrt{3}+\sqrt{3}}{4\sqrt{3}}=\frac{5}{4}$,
故$x + y\in\left[\frac{3}{4}, \frac{5}{4}\right]$.

解法2:以D为原点,DB,DA所在直线分别为x轴、y轴建立直角坐标系,如图2所示,则$C(-4, 0)$,$B(4, 0)$,$E(2, 0)$,$A(0, 4\sqrt{3})$.
因为点Q所在圆的方程为$(x - 2)^2 + y^2 = 3$,所以可设$Q(2+\sqrt{3}\cos\theta, \sqrt{3}\sin\theta)$,
所以$\overrightarrow{AC}=(-4, -4\sqrt{3})$,$\overrightarrow{AB}=(4, -4\sqrt{3})$,$\overrightarrow{AQ}=(2+\sqrt{3}\cos\theta, \sqrt{3}\sin\theta - 4\sqrt{3})$.
因为$\overrightarrow{AQ}=x\overrightarrow{AB}+y\overrightarrow{AC}$,所以$-4\sqrt{3}x - 4\sqrt{3}y=\sqrt{3}\sin\theta - 4\sqrt{3}$,即$x + y = 1-\frac{\sin\theta}{4}$.
所以由$\sin\theta\in[-1, 1]$,可得$x + y\in\left[\frac{3}{4}, \frac{5}{4}\right]$.

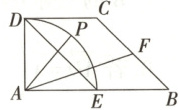
6.如图,在直角梯形$ABCD$中,$AB\perp AD$,$DC// AB$,$AD = DC = 1$,$AB = 2$,$E,F$分别为$AB,BC$的中点,点$P$在以$A$为圆心的圆弧$\overset\frown{DE}$上运动,若$\overrightarrow{AP}=x\overrightarrow{ED}+y\overrightarrow{AF}$,求$2x - y$的取值范围.

答案:
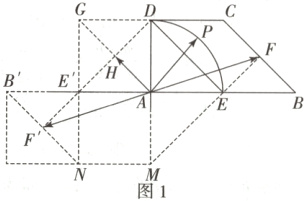
6.解法1(等和线):如图1所示,延长CD到G,使$DG = CD$,延长BA到B',使$AB' = BA$,延长FE交DA的延长线于点M,作线段MN平行且等于DG,连接NB',点H,F'分别是线段AG,B'N的中点,则$\overrightarrow{AF}=-\overrightarrow{AF'}$,$\overrightarrow{ED}=2\overrightarrow{AH}$,所以$\overrightarrow{AP}=2x\overrightarrow{AH}-y\overrightarrow{AF'}$.
令点P所在的直线l平行于HF',由等和线的性质可知,当点P与点D重合时,P,H,F'三点共线,此时$2x - y$取到最大值1;当点P与E重合时,易知F,P,M三点共线,且$FM// DF'$,此时$2x - y$取到最小值 - 1(因为$\overrightarrow{AF}=-\overrightarrow{AF'}$,故$2x - y = k = - \frac{\overrightarrow{AF}}{\overrightarrow{AF'}}=-1$),所以$2x - y\in[-1, 1]$.
解法2:建立如图2所示的坐标系,则$A(0, 0)$,$E(1, 0)$,$D(0, 1)$,$F(1.5, 0.5)$,$P(\cos\alpha, \sin\alpha)(0^{\circ}\leqslant\alpha\leqslant90^{\circ})$.
∵$\overrightarrow{AP}=x\overrightarrow{ED}+y\overrightarrow{AF}$,
∴$(\cos\alpha, \sin\alpha)=x(-1, 1)+y(1.5, 0.5)$,
∴$\begin{cases} \cos\alpha=-x + 1.5y \\ \sin\alpha=x + 0.5y \end{cases}$,
∴$\begin{cases} x=\frac{1}{4}(3\sin\alpha-\cos\alpha) \\ y=\frac{1}{2}(\cos\alpha+\sin\alpha) \end{cases}$,
∴$2x - y=\sin\alpha-\cos\alpha=\sqrt{2}\sin(\alpha - 45^{\circ})$.
∵$0^{\circ}\leqslant\alpha\leqslant90^{\circ}$,
∴$-45^{\circ}\leqslant\alpha - 45^{\circ}\leqslant45^{\circ}$,
∴$-\frac{\sqrt{2}}{2}\leqslant\sin(\alpha - 45^{\circ})\leqslant\frac{\sqrt{2}}{2}$,
∴$-1\leqslant\sqrt{2}\sin(\alpha - 45^{\circ})\leqslant1$,
∴$2x - y$的取值范围是$[-1, 1]$.

6.解法1(等和线):如图1所示,延长CD到G,使$DG = CD$,延长BA到B',使$AB' = BA$,延长FE交DA的延长线于点M,作线段MN平行且等于DG,连接NB',点H,F'分别是线段AG,B'N的中点,则$\overrightarrow{AF}=-\overrightarrow{AF'}$,$\overrightarrow{ED}=2\overrightarrow{AH}$,所以$\overrightarrow{AP}=2x\overrightarrow{AH}-y\overrightarrow{AF'}$.
令点P所在的直线l平行于HF',由等和线的性质可知,当点P与点D重合时,P,H,F'三点共线,此时$2x - y$取到最大值1;当点P与E重合时,易知F,P,M三点共线,且$FM// DF'$,此时$2x - y$取到最小值 - 1(因为$\overrightarrow{AF}=-\overrightarrow{AF'}$,故$2x - y = k = - \frac{\overrightarrow{AF}}{\overrightarrow{AF'}}=-1$),所以$2x - y\in[-1, 1]$.

解法2:建立如图2所示的坐标系,则$A(0, 0)$,$E(1, 0)$,$D(0, 1)$,$F(1.5, 0.5)$,$P(\cos\alpha, \sin\alpha)(0^{\circ}\leqslant\alpha\leqslant90^{\circ})$.
∵$\overrightarrow{AP}=x\overrightarrow{ED}+y\overrightarrow{AF}$,
∴$(\cos\alpha, \sin\alpha)=x(-1, 1)+y(1.5, 0.5)$,
∴$\begin{cases} \cos\alpha=-x + 1.5y \\ \sin\alpha=x + 0.5y \end{cases}$,
∴$\begin{cases} x=\frac{1}{4}(3\sin\alpha-\cos\alpha) \\ y=\frac{1}{2}(\cos\alpha+\sin\alpha) \end{cases}$,
∴$2x - y=\sin\alpha-\cos\alpha=\sqrt{2}\sin(\alpha - 45^{\circ})$.
∵$0^{\circ}\leqslant\alpha\leqslant90^{\circ}$,
∴$-45^{\circ}\leqslant\alpha - 45^{\circ}\leqslant45^{\circ}$,
∴$-\frac{\sqrt{2}}{2}\leqslant\sin(\alpha - 45^{\circ})\leqslant\frac{\sqrt{2}}{2}$,
∴$-1\leqslant\sqrt{2}\sin(\alpha - 45^{\circ})\leqslant1$,
∴$2x - y$的取值范围是$[-1, 1]$.

查看更多完整答案,请扫码查看


