《2025年全国重点高中提前招生同步强化全真试卷八年级数学上册》

1. (黄冈中学自主招生)设 $ a,b,c $ 分别是 $ \triangle ABC $ 的三条边,对应的角分别为 $ A,B,C $,若 $ b = 3,c = 2,C = 30° $,则可以作出符合条件的三角形的个数为 (C)

A.0
B.1
C.2
D.不确定

答案：
1. C 提示：如图2 - 1，过A点作AD⊥BC于D，
∵∠C = 30°，AC = b = 3，
∴AD = $\frac{1}{2}$AC = 1.5。
∵AB = c = 2，
∴符合条件的B点有两个，所以可以作出符合条件的三角形的个数为2个，故选C。

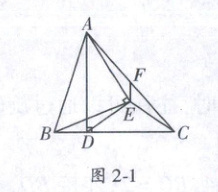
2. (福建泉州市永春县自主招生)如图 2 - 1,已知 $ AD $ 为 $ \triangle ABC $ 的高,$ AD = BC $,以 $ AB $ 为底边作等腰直角三角形 $ ABE $,$ EF // AD $,交 $ AC $ 于点 $ F $,连接 $ ED,EC $,有以下结论:① $ \triangle ADE \cong \triangle BCE $;② $ CE \perp AB $;③ $ BD = 2EF $;④ $ S_{\triangle BDE} = S_{\triangle ACE} $.其中正确的是 (D)

A.①②③
B.②④
C.①③
D.①③④

答案： 2. D 提示：延长CE交AD于K，交AB于H；设AD交BE于O。
∵∠ODB = ∠OEA，∠AOE = ∠DOB，
∴∠OAE = ∠OBD。
∵AE = BE，AD = BC，
∴△ADE≌△BCE，故①正确；
∵∠AED = ∠BEC，DE = EC，∠AEB = ∠DEC = 90°，
∴∠ECD = ∠ABE = 45°。
∵∠AHC = ∠ABC + ∠HCB = 90° + ∠EBC＞90°，
∴EC不垂直AB，故②错误；
∵∠AEB = ∠HED，
∴∠AEK = ∠BED。
∵AE = BE，∠KAE = ∠EBD，
∴△KAE≌△DBE，
∴BD = AK；
∵△DCK是等腰直角三角形，DE平分∠CDK，
∴EC = EK。
∵EF//AK，
∴AF = FC，
∴AK = 2EF，
∴BD = 2EF，故③正确；
∵EK = EC，
∴S△AKE = S△AEC。
∵△KAE≌△DBE，
∴S△KAE = S△BDE，
∴S△BDE = S△AEC，故④正确，故选D。

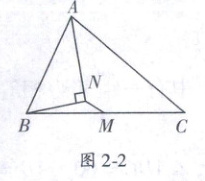
3. (乐平市自主招生)如图 2 - 2,$ M $ 是 $ \triangle ABC $ 的边 $ BC $ 的中点,$ AN $ 平分 $ \angle BAC $,$ BN \perp AN $ 于点 $ N $,且 $ AB = 10,BC = 15,MN = 3 $,则 $ \triangle ABC $ 的周长是 (D)

A.38
B.39
C.40
D.41

答案： 3. D 提示：延长BN交AC于点D，
∵AN平分∠BAC，BN⊥AN于点N，在Rt△ANB和Rt△AND中，∠BAN = ∠DAN，∠ANB = ∠AND，AN = AN，
∴△ANB≌△AND(ASA)，
∴AD = AB = 10，BN = DN，即N为BD的中点。
∵M是△ABC的边BC的中点，
∴CD = 2MN = 6，△ABC的周长为AB + AC + BC = 10 + (10 + 6) + 15 = 41。故选D。

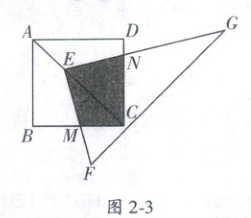
4. (山西中考)如图 2 - 3,点 $ E $ 在正方形 $ ABCD $ 的对角线 $ AC $ 上,且 $ EC = 2AE $,直角三角形 $ FEG $ 的两直角边 $ EF,EG $ 分别交 $ BC,DC $ 于点 $ M,N $.若正方形 $ ABCD $ 的边长为 $ a $,则重叠部分四边形 $ EMCN $ 的面积为 (D)

A.$ \frac{2}{3}a^2 $
B.$ \frac{1}{4}a^2 $
C.$ \frac{5}{9}a^2 $
D.$ \frac{4}{9}a^2 $

答案： 4. D 提示：过E作EP⊥BC于点P，EQ⊥CD于点Q，
∵四边形ABCD是正方形，
∴∠BCD = 90°。又
∵∠EPM = ∠EQN = 90°，∠PEM + ∠MEQ = 90°。三角形FEG是直角三角形，
∴∠NEF = ∠NEQ + ∠MEQ = 90°，
∴∠PEM = ∠NEQ。
∵AC是∠BCD的角平分线，∠EPC = ∠EQC = 90°，
∴EP = EQ，四边形PCQE是正方形，得△EPM≌△EQN，
∴S△EQN = S△EPM，四边形EMCN的面积等于正方形PCQE的面积。
∵正方形ABCD的边长为a，AC = $\sqrt{2}a$，EC = 2AE，
∴EC = $\frac{2\sqrt{2}}{3}a$，EP = PC = $\frac{2}{3}a$，正方形PCQE的面积 = $\frac{2}{3}a×\frac{2}{3}a = \frac{4}{9}a²$，故选D。

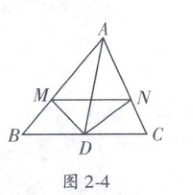
5. (湛江市霞山区自主招生)如图 2 - 4,在 $ \triangle ABC $ 中,$ AD $ 为 $ BC $ 边上中线,$ DM,DN $ 分别是 $ \angle ADB,\angle ADC $ 的角平分线,试比较 $ BM + CN $ 与 $ MN $ 的大小关系 (C)

A.$ BM + CN = MN $
B.$ BM + CN ＜ MN $
C.$ BM + CN ＞ MN $
D.无法确定

答案：
5. C 提示：如图2 - 2，延长ND至P，使DP = ND，连接MP，BP，
∵点D为BC的中点，
∴BD = CD。又
∵∠BDP = ∠CDN，
∴△BDP≌△CDN(SAS)，
∴BP = CN。
∵DM，DN分别是∠ADB，∠ADC的角平分线，∠ADB + ∠ADC = 180°，
∴∠ADM + ∠ADN = $\frac{1}{2}×180° = 90°$，
∴MD⊥PN。
∵DP = DN，
∴MN = MP。
∵BM + BP ＞ MP，
∴BM + CN ＞ MN。故选C。

6. (2023·浙江诸暨自主招生)在四边形 $ ABCD $ 中,对角线 $ AC $ 与 $ BD $ 相交于点 $ E $,若 $ AC $ 平分 $ \angle DAB $,$ AB = AE,AC = AD $.那么在下列四个结论中:① $ AC \perp BD $;② $ BC = DE $;③ $ \angle DBC = \frac{1}{2}\angle DAB $;④ $ \triangle ABE $ 是正三角形.其中正确的是 (B)

A.①和②
B.②和③
C.③和④
D.①和④

答案：
6. B 提示：如图2 - 3，

∵AB = AE，一个三角形的直角边和斜边一定不相等，
∴AC不垂直于BD，①错误；利用边角边定理可证得△ADE≌△ABC，那么BC = DE，②正确；由△ADE≌△ABC可得∠ADE = ∠ACB，那么A，B，C，D四点共圆，
∴∠DBC = ∠DAC = $\frac{1}{2}$∠DAB，③正确；△ABE不一定是等边三角形，那么④不一定正确。故选B。

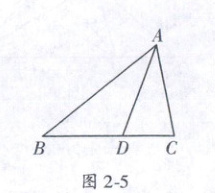
7. (四川初中数学竞赛)如图 2 - 5,在 $ \triangle ABC $ 中,$ AD $ 是 $ \angle BAC $ 的平分线,且 $ AB = AC + CD $,若 $ \angle BAC = 60° $,则 $ \angle ABC $ 的大小为 (A)

A.$ 40° $
B.$ 60° $
C.$ 80° $
D.$ 100° $

答案： 7. A 提示：解法一：在AB上取AC' = AC，
∵AD是角平分线，
∴△ACD≌△AC'D，又AB = AC + CD，得AB = AC' + C'D，故BC' = C'D，∠C = ∠ACD = 2∠B，又∠B + ∠C = 180° - ∠A = 120°，故∠B = 40°。解法二：延长AC至点E，使得CE = CD，连接DE，AB = AC + CD = AC + CE = AE，
∵AD是角平分线，
∴∠BAD = ∠EAD，又AD = AD，△ABD≌△AED(SAS)，∠E = ∠B。CE = CD，
∴∠CDE = ∠DCE，∠ACD = 2∠E = 2∠B，
∵∠ADC = ∠B + ∠BAD = ∠B + 30°，∠DAC = 30°，在△ADC中由三角形的内角和得∠B + 30° + 30° + 2∠B = 180°，故∠B = 40°。