《2025年全国重点高中提前招生同步强化全真试卷八年级数学上册》

1. (四川成都自主招生) 设 $ A,B,C,D $ 为平面上任意四点, 如果其中任意三点不在同一直线上, 则 $ \triangle ABC,\triangle ABD,\triangle ACD,\triangle BCD $ 中至少存在一个三角形的某个内角满足 (C)

A.不超过 $ 15^{\circ} $
B.不超过 $ 30^{\circ} $
C.不超过 $ 45^{\circ} $
D.以上都不对

答案： 1.C　提示:△ABC,△ABD,△ACD,△BCD中至少存在一个三角形的某个内角满足不超过45°,证明如下:
　假设A,B,C,D四点，任选三点构成的三角形的三个内角都大于45°,当ABCD构成凸四边形时，可得各角和大于360°，与四边形内角和等于360°矛盾;当ABCD构成凹四边形时，可得三角形内角和大于180°，与三角形内角和等于180°矛盾.故在△ABC，△ABD,△ACD,△BCD中至少有一个三角形的内角不超过45°.故选C.

2. (成都市武侯区自主招生) 若一个三角形的三边和为 40, 且各边长均为整数, 则符合条件的三角形的个数为 (C)

A.31
B.32
C.33
D.34

答案： 2.C　提示:根据题意得三角形的三边都小于20,设最小的两边为x≤y≤19,x+y＞20　当x=2时,y=19,当x=3时,y=18,当x=4时,y=17,18,当x=5时,y=16,17,当x=6时,y=15,16,17,当x=7时,y=14,15,16,当x=8时,y=13,14,15,16,当x=9时,y=12,13,14,15,当x=10时,y=11,12,13,14,15,当x=11时,y=11,12,13,14,当x=12时,y=12,13,14,当x=13时,y=13,符合条件的三角形的个数为1+1+2+2+3+3+4+4+5+4+3+1=33.故选C.

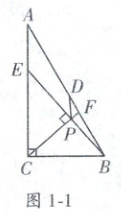
3. (2024·蚌埠三模) 如图 1 - 1, 在 $ Rt\triangle ABC $ 中, $ \angle ACB = 90^{\circ},AC = 5,BC = 3 $, $ D $ 是 $ AB $ 的中点, $ E $ 为射线 $ CA $ 上一动点. 过点 $ C $ 作 $ CP \perp BE $ 于点 $ P $, 交 $ AB $ 于点 $ F $, 则 $ DP $ 长度的最小值是 (B)

A.$ \sqrt{5} $
B.1
C.$ \sqrt{3} $
D.$ \sqrt{5} - 2 $

答案：
3.B　提示:如图1−1,取CB的中点O,连接OP,DO,由∠ACB=90°,AC=5,BC=3,D是AB的中点,CP⊥BE,得DO=$\frac{1}{2}$AC=2.5,PO=$\frac{1}{2}$CB=1.5,得DP≥DO−PO=2.5−1.5=1(仅当D,P,O三点共线时取等号).故选B.

4. 把一个多边形纸片沿一条直线剪下一个三角形后, 变成一个 18 边形, 则原多边形的边数不可能是 (A)

A.16
B.17
C.18
D.19

答案： 4.A　提示:一个n边形剪去一个角后，剩下的形状可能是n边形或(n+1)边形或(n−1)边形,所以当剪去一个角后,剩下的部分是一个18边形，则这张纸片原来的形状可能是18边形或17边形或19边形，不可能是16边形.故选A.

5. (2023·浙江慈溪中学核心素养测试) 把一根长为 100 cm 的铁丝截成 $ n $ 小段 $ (n \geq 3) $, 每段长不小于 10 cm, 若对不论怎样的截法, 总存在 3 小段. 以它们为边可拼成一个三角形, 则 $ n $ 的最小值是 (B)

A.4
B.5
C.6
D.7

答案： 5.B　提示:先假设截取的小段从短到长排列依次是a₁,a₂,a₃,a₄,a₅,…,a₁₀；
∵每一段不小于10cm,
∴a₁+a₂≥20,a₃不与前两段组成三角形的话,a₃≥a₁+a₂,即a₃≥20,a₄不与前三段的任意两段构成三角形的话,必须大于任意两段之和,即a₄≥a₃+a₂,即a₄≥30,此时剩下的a₅≤100−10−10−20−30=30,那么前面四段中必有两段与a₅组成三角形.
∴n的最小值为5.故选B.

6. (2022·深圳市第九届“鹏程杯”邀请赛) 已知三角形三边的长分别为 $ a,b,c $, 且 $ a,b,c $ 均为整数, 若 $ b = 7,a ＜ b $, 则满足条件的不同形状的三角形的个数是 (A)

A.30
B.36
C.40
D.42
E.45

答案： 6.A　提示:
∵三角形的三边a,b,c的长都是整数,且a＜b,b=7,
∴a=1,2,3,4,5,6.根据三角形的三边关系,得b−a＜c＜b+a,即7−a＜c＜7+a.当a=1时,6＜c＜8,则c=7,此时满足条件的三角形有1个;当a=2时,5＜c＜9,则c=6,7,8,此时满足条件的三角形有3个;当a=3时，4＜c＜10,则c=5,6,7,8,9,此时满足条件的三角形有5个;当a=4时,3＜c＜11,则c=4,5,6,7,8,9,10,此时满足条件的三角形有7个;当a=5时,2＜c＜12,则c=3,4,5,6,7,8,9,10,11,此时满足条件的三角形有9个;当a=6时，1＜c＜13,则c=2,3,4,5,6,7,8,9,10,11,12,此时满足条件的三角形有11个.
∵边长一样，形状应该一样,其中2,6,7重复一次;3,6,7重复一次;3,5,7重复一次;4,5,7重复一次;4,6,7重复一次;5,6,7重复一次,
∴满足条件的三角形一共有1+3+5+7+9+11−6=30 (个).故选A.

7. (宁波重点中学保送生招生考试) 用三种边长相等的正多边形地砖铺地, 其顶点拼在一起, 刚好能完全铺满地面. 已知正多边形的边数分别为 $ x,y,z $. 则 $ \frac{1}{x} + \frac{1}{y} + \frac{1}{z} $ 的值为 (C)

A.1
B.$ \frac{2}{3} $
C.$ \frac{1}{2} $
D.$ \frac{1}{3} $

答案： 7.C　提示:由题意知,这三种多边形的3个内角之和为360°,已知正多边形的边数为x,y,z,那么这3个内角和可表示为$\frac{(x - 2)×180}{x}+\frac{(y - 2)×180}{y}+\frac{(z - 2)×180}{z}=360$,两边都除以180得$1-\frac{2}{x}+1-\frac{2}{y}+1-\frac{2}{z}=2$,两边都除以2得$\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{1}{2}$.故选C.

8. (成都青羊区自主招生) 已知 7 条长度分别为整数 $ a_1,a_2,·s,a_7 $ 的线段, 它们中的任意三条都不能构成三角形, 若 $ a_1 = 1 ＜ a_2 ＜ a_3 ＜ a_4 ＜ a_5 ＜ a_6 ＜ a_7 = 21 $, 则 $ a_6 = $ (B)

A.18
B.13
C.8
D.5

答案： 8.B　提示:不能构成三角形，那么前两个数之和小于或等于第三个数字，最小的a₁是1,最小情况如下:1,2,3,5,8,13,21,34满足条件若a₁=1cm,a₇=21cm,则a₆=13cm.故选B.

9. (温州市初中数学竞赛能力检测) 某同学用纸剪凸四边形, 凸五边形, 凸六边形, 每种至少剪一个, 剪出的多边形共有 95 条边, 那么所剪的多边形中的内角是直角的个数最多是90_ 个.

答案： 9.90　提示:由多边形的内角和可知四边形最多有四个直角，五边形和六边形最多有三直角，剪一个凸四边形，一个凸五边形，一个凸六边形共有15条边,4+3+3=10个直角，剩下95−15=80条边都是四边形并且都是矩形直角最多，80条边组成20个矩形，共有80个直角，所以，所剪的多边形中的内角是直角的个数最多是10+80=90.

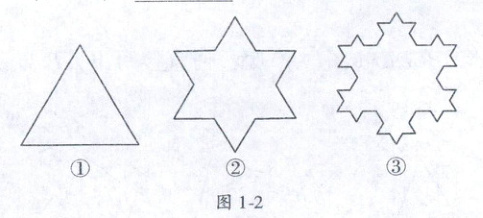
10. (2022·华师一附中自主招生) 2022 年冬奥会在北京胜利召开, 开幕式上, “雪花引导牌”以线条造型展现出简洁、空灵、浪漫的冰雪美学. 其中雪花造型惊艳全球, “雪花”图形的作法是: 从一个正三角形开始, 把每条边分成三等份, 然后以各边中间一段为底边分别向外作正三角形, 再去掉底边. 反复进行这一过程, 就得到一条“雪花”状的曲线. 设原正三角形 (图①) 的边长为 1, 把图①, 图②, 图③中图形的周长依次记为 $ C_1,C_2,C_3 $, 将图③继续进行这一过程, 得到的曲线的周长记为 $ C_4 $, 则 $ C_4 =$$\frac{64}{9}$$$ _.

答案： 10.$\frac{64}{9}$　提示:观察发现:第二个图形在第一个图形的周长的基础上多了它的周长的$\frac{1}{3}$,即为$\frac{4}{3}·3a$,第三个在第二个的基础上，多了其周长的$\frac{1}{3}$,即$(\frac{4}{3})^2·3a$,依次类推，则得到的第四个图形的周长是第一个图形周长的$(\frac{4}{3})^{(4 - 1)}·3a$,故$C_4=(\frac{4}{3})^{(4 - 1)}×3×1=\frac{64}{9}$.