《2025年全国重点高中提前招生同步强化全真试卷八年级数学上册》

17. (山东枣庄自主招生)(1)阅读理解:
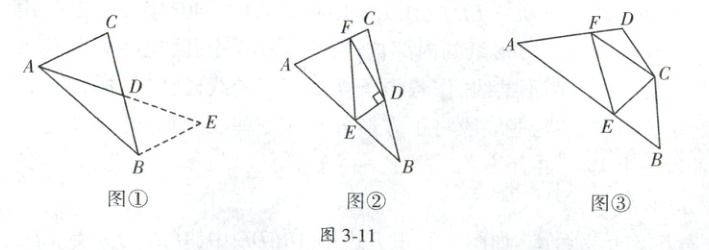
如图①,在△ABC 中,若 AB = 10,AC = 6,求 BC 边上的中线 AD 的取值范围.
解决此问题可以用如下方法:延长 AD 到点 E 使 DE = AD,再连接 BE(或将△ACD 绕着点 D 逆时针旋转 180°得到△EBD),把 AB,AC,2AD 集中在△ABE 中,利用三角形三边的关系即可判断. 中线 AD 的取值范围是2＜AD＜8;
(2)问题解决:
如图②,在△ABC 中,D 是 BC 边上的中点,DE⊥DF 于点 D,DE 交 AB 于点 E,DF 交 AC 于点 F,连接 EF,求证:BE + CF ＞ EF;
(3)问题拓展:
如图③,在四边形 ABCD 中,∠B + ∠D = 180°,CB = CD,∠BCD = 140°,以 C 为顶点作一个 70°角,角的两边分别交 AB,AD 于 E,F 两点,连接 EF,探索线段 BE,DF,EF 之间的数量关系,并加以证明.

答案：
17.
(1)解:延长AD至E，使DE = AD，连接BE，
∵AD是BC边上的中线，
∴BD = CD，
∴△BDE≌△CDA(SAS)，
∴BE = AC = 6，在△ABE中，由三角形的三边关系得AB - BE＜AE＜AB + BE，
∴10 - 6＜AE＜10 + 6，即4＜AE＜16，
∴2＜AD＜8;
(2)证明:延长FD至点M，使DM = DF，连接BM，EM，如图3 - 9①所示:同
(1)得△BMD≌△CFD(SAS)，
∴BM = CF.
∵DE⊥DF，DM = DF，
∴EM = EF，在△BME中，由三角形的三边关系得BE + BM＞EM，
∴BE + CF＞EF;
(3)解:BE + DF = EF，理由如下:延长AB至点N，使BN = DF，连接CN，如图3 - 9②所示:
∵∠ABC + ∠D = 180°，∠NBC + ∠ABC = 180°，
∴∠NBC = ∠D，
∴△NBC≌△FDC(SAS)，
∴CN = CF，∠NCB = ∠FCD，
∵∠BCD = 140°，∠ECF = 70°，
∴∠BCE + ∠FCD = 70°，
∴∠ECN = 70° = ∠ECF，
∴△NCE≌△FCE(SAS)，
∴EN = EF，
∵BE + BN = EN，
∴BE + DF = EF.

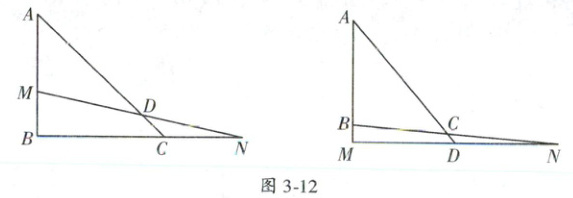
18. (华师一附中自主招生)如图 3 - 12,已知 Rt△ABC 的三边满足$(AB - 4)^2 + |AB - BC| = 0$,∠ABC = 90°.
(1)若 M 是边 AB 上一点,N 是边 BC 延长线上一点,且线段 AM = CN = m,$\frac{m}{AB - m} = \frac{AB}{BC} + 2$,求 m 的值;
(2)若 M 是边 AB 上一动点,N 是边 BC 延长线上一动点,且线段 AM = CN,判断线段 DM 与 DN 的大小关系,并说明你的理由;
(3)若 M,N 分别是边 AB,BC 延长线上的动点,D 为线段 MN 与边 AC 延长线的交点,线段 AM = CN,判断线段 DM 与 DN 的大小关系,并说明你的理由.

答案：
18.解:
(1)
∵AB - 4 = 0且AB - BC = 0，
∴AB = BC = 4.
∵$\frac{m}{AB - m}$ = $\frac{AB}{BC}$ + 2，
∴$\frac{m}{4 - m}$ = 1 + 2 = 3，
∴m = 3，经检验得m = 3.
(2)DM = DN，理由如下:如图3 - 10图1，过M作ME⊥AB交AC于E，
∵AB = BC，∠B = 90°，
∴∠A = ∠ACB = 45°，∠AEM = 90° - ∠A = 45°，
∴AM = ME，
∵AM = CN，
∴ME = CN.
∵∠AME = ∠B = 90°，
∴ME//BC，
∴∠EMD = ∠N，
∴△EMD≌△CND(AAS)，
∴DM = DN.
(3)DM = DN，理由如下:如图3 - 10图2，过M作MH⊥AM交AD的延长线于H，同
(2)可证:DM = DN.