《2025年全国重点高中提前招生同步强化全真试卷八年级数学上册》

15. (浙江鼓楼区自主招生)记三角形三边长为$a$,$b$,$c$,对应边上的高为$h_a$,$h_b$,$h_c$,请解答:
(1)已知$h_a:h_b:h_c = 2:3:4$,且这三角形周长为$26cm$,求$a$,$b$,$c$.
(2)若三角形的三条高分别为$2$,$x$,$6$,求$x$的取值范围.
(3)若三条高分别为$2$,$x$,$6$的三角形是等腰三角形,求$x$.

答案： 15.解：
(1)设$h_a = 2k$，$h_b = 3k$，$h_c = 4k$，则$\frac{1}{2}ah_a = \frac{1}{2}bh_b = \frac{1}{2}ch_c$，即$\frac{1}{2} × a × 2k = \frac{1}{2} × b × 3k = \frac{1}{2} × c × 4k$，$\therefore 2a = 3b = 4c$，$\therefore a:b:c = 6:4:3$；又$\because a + b + c = 26cm$，$\therefore a = 12cm$，$b = 8cm$，$c = 6cm$；
(2)设三角形的面积为$s$，则$s = \frac{1}{2}ah_a = a$，$s = \frac{1}{2}bh_b = \frac{1}{2} × b × 3k$，$s = \frac{1}{2}ch_c = \frac{1}{2} × c × 4k$，$\therefore a = s$，$b = \frac{2s}{3}$，$c = \frac{s}{2}$，又$a - c \lt b \lt a + c$，即$s - \frac{s}{2} \lt \frac{2s}{3} \lt s + \frac{s}{2}$，$\frac{s}{2} \lt \frac{2s}{3} \lt \frac{3s}{2}$，$\frac{1}{3} \lt \frac{2}{3} \lt \frac{3}{2}$，$\frac{3}{2} \lt x \lt 3$；
(3)设三角形的面积为$s$，由
(2)知$a = s$，$b = \frac{2s}{x}$，$c = \frac{s}{3}$，显然$a \gt c$，分两种情况：①如果$a = b$，那么$s = \frac{2s}{x}$，解得$x = 2$；②如果$b = c$，那么$b + c \lt a$，不满足三角形三边关系定理，故舍去.故所求$x = 2$.

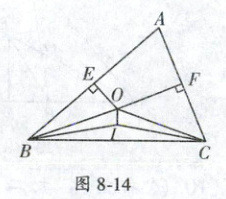
16. (靖江市月考)如图 8 - 14,$OE$,$OF$分别是$\triangle ABC$中$AB$,$AC$边的中垂线(即垂直平分线),$\angle OBC$,$\angle OCB$的平分线相交于点$I$,试判定$OI$与$BC$的位置关系,并给出证明.

答案：
16.解：$OI \perp BC$. 理由：如图8−8，连接$OA$，过点$I$作$IM \perp OB$于点$M$，过点$I$作$IN \perp OC$于点$N$，过点$I$作$IG \perp BC$于点$G$，$\because OE$，$OF$分别是$AB$，$AC$边的中垂线，$\therefore OA = OB$，$OA = OC$，$\therefore OB = OC$，$\because \angle OBC$，$\angle OCB$的平分线相交于点$I$，$\therefore IM = IG$，$IN = IG$，$\therefore IM = IN$，$\therefore$点$I$在$\angle BOC$的角平分线上，$\because OB = OC$，$\therefore OI \perp BC$.
　　

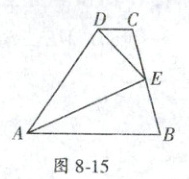
17. (2022·西安碑林区期末)如图 8 - 15,在四边形$ABCD$中,$AB// CD$,点$E$是$BC$的中点,$DE$平分$\angle ADC$. 求证:$AE$是$\angle DAB$的平分线.

答案：
17.解：如图8−9，过点$E$作$EH \perp AB$于点$H$，反向延长$EH$交$DC$的延长线于点$G$，过点$E$作$EF \perp AD$于点$F$，$\because AB // CD$，$EH \perp AB$，$\therefore EG \perp DC$，$\because$点$E$是$BC$的中点，$\therefore CE = BE$，易证$\triangle CGE \cong \triangle BHE$，$GE = EH$，$\because DE$平分$\angle ADC$，$\therefore GE = EF$，$\therefore EF = EH$，$\therefore AE$是$\angle DAB$的平分线.