《2025年全国重点高中提前招生同步强化全真试卷八年级数学上册》

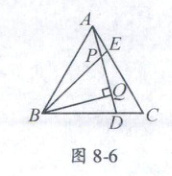
7. 如图 8 - 6,$\triangle ABC$为等边三角形,$AE = CD$,$AD$,$BE$相交于点$P$,$BQ\perp AD$于点$Q$,$PQ = 3$,$PE = 1$,则$AD$的长是(D)

A.4
B.5
C.6
D.7

答案： 7.D 提示：$\because \triangle ABC$为等边三角形，$\therefore \angle BAC = \angle C = 60^{\circ}$，$AB = AC$，又$\because AE = CD$，$\therefore \triangle ABE \cong \triangle CAD(SAS)$，$\therefore \angle ABE = \angle CAD$，$BE = AD$，$\angle BPQ = \angle BAP + \angle ABE = \angle BAP + \angle CAD = \angle BAC = 60^{\circ}$，又$\because BQ \perp PQ$，$\therefore \angle BQP = 90^{\circ}$，$\angle PBQ = 30^{\circ}$，$\therefore PB = 2PQ = 6$，$\therefore BE = BP + PE = 6 + 1 = 7$，$\therefore AD = BE = 7$.

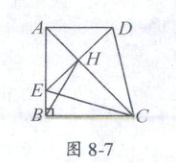
8. 如图 8 - 7,在直角梯形$ABCD$中,$AD// BC$,$\angle ABC = 90^{\circ}$,$AB = BC$,$E$为$AB$边上一点,$\angle BCE = 15^{\circ}$,且$AE = AD$. 连接$DE$交对角线$AC$于$H$,连接$BH$. 下列结论:①$\triangle ACD\cong \triangle ACE$;②$\triangle CDE$为等边三角形;③$\frac{EH}{BE} = 2$;④$\frac{S_{\triangle EBC}}{S_{\triangle EHC}} = \frac{AH}{CH}$. 其中正确的是(B)

A.①②
B.①②④
C.③④
D.①②③④

答案： 8.B 提示：$\because AD // BC$，$AB = BC$，$\angle ABC = 90^{\circ}$，$\therefore \angle BAC = \angle ACB = \angle CAD = 45^{\circ}$，又$\because AE = AD$，$\therefore \angle AEH = \angle ADH = 45^{\circ}$，$\therefore AC \perp DE$，又$\angle BCE = 15^{\circ}$，$\angle HCE = 30^{\circ}$，$\therefore \angle DEC = 60^{\circ}$，在$Rt\triangle HEC$中，$EH = \frac{1}{2}EC$，$\therefore DE = EC$，$\therefore \triangle CDE$为等边三角形，且$\triangle ACD \cong \triangle ACE$. 故有①②④正确.

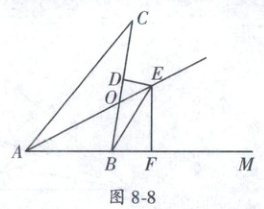
9. (2023·福建龙岩长汀六校联考)如图 8 - 8,$AE$是$\angle CAM$的角平分线,点$B$在射线$AM$上,$DE$是线段$BC$的中垂线交$AE$于点$E$,$EF\perp AM$. 若$\angle ACB = 26^{\circ}$,$\angle CBE = 25^{\circ}$,则$\angle AED = $39°.

答案：
9.39° 提示：如图8−5，连接$CE$，过$E$作$ER \perp AC$于$R$，交$CD$于$Q$，$AE$交$BC$于$O$，$\because DE$是线段$BC$的中垂线，$\therefore \angle EDC = 90^{\circ}$，$CE = BE$，$\angle ECB = \angle CBE$，$\because \angle CBE = 25^{\circ}$，$\therefore \angle ECB = 25^{\circ}$，$\therefore \angle DEB = \angle CED = 90^{\circ} - 25^{\circ} = 65^{\circ}$，$\because ER \perp AC$，$ED \perp BC$，$\therefore \angle QRC = \angle QDE = 90^{\circ}$，$\therefore \angle ACB + \angle CQR = 90^{\circ}$，$\angle EQD + \angle QED = 90^{\circ}$，$\because \angle CQR = \angle EQD$，$\therefore \angle ACB = \angle QED$，$\because \angle ACB = 26^{\circ}$，$\therefore \angle QED = 26^{\circ}$，$\because AE$平分$\angle CAM$，$ER \perp AC$，$EF \perp AM$，$\therefore ER = EF$，在$Rt\triangle ERC$和$Rt\triangle EFB$中，$CE = BE$，$ER = EF$，$\therefore Rt\triangle ERC \cong Rt\triangle EFB(HL)$，$\therefore \angle EBF = \angle ACE = \angle ACB + \angle ECD = 26^{\circ} + 25^{\circ} = 51^{\circ}$，$\because \angle EFB = 90^{\circ}$，$\therefore \angle BEF = 90^{\circ} - \angle EBF = 90^{\circ} - 51^{\circ} = 39^{\circ}$，$\therefore \angle REF = \angle RED + \angle BED + \angle BEF = 26^{\circ} + 65^{\circ} + 39^{\circ} = 130^{\circ}$，$\because \angle ARE = \angle AFE = 90^{\circ}$，$\therefore \angle CAM = 360^{\circ} - 90^{\circ} - 90^{\circ} - 130^{\circ} = 50^{\circ}$，$\because AE$平分$\angle CAM$，$\therefore \angle CAE = \frac{1}{2}\angle CAM = 25^{\circ}$，$\therefore \angle DOE = \angle CAE + \angle ACB = 25^{\circ} + 26^{\circ} = 51^{\circ}$，$\because ED \perp BC$，$\angle EDB = 90^{\circ}$，$\therefore \angle AED = 90^{\circ} - \angle DOE = 90^{\circ} - 51^{\circ} = 39^{\circ}$，故答案为$39^{\circ}$.
　　

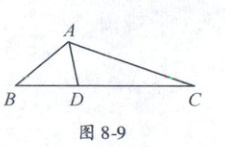
10. (“希望杯”初二竞赛)如图 8 - 9,已知$\triangle ABC$中,$AD$平分$\angle BAC$,$\angle C = 20^{\circ}$,$AB + BD = AC$,则$\angle B$的度数为40°.

答案： 10.40° 提示：在$AC$上截取$AE = AB$，连接$DE$，则可证$\triangle ABD \cong \triangle AED$，$\therefore BD = DE$，$\angle B = \angle AED$，$\because AB + BD = AC$，$\therefore AB + DE = AC$，$\because CE = DE$，$\therefore \angle EDC = \angle C = 20^{\circ}$，$\therefore \angle B = \angle AED = 40^{\circ}$.

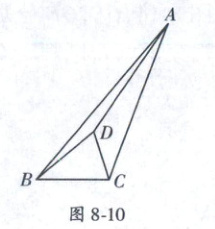
11. (“学而思杯”中学生理科能力大赛)如图 8 - 10,已知$AB = a$,$BD = b$,$(a,b$为常数),$BC = BD$,$\angle ABD:\angle BAC:\angle ACD:\angle CBD = 1:2:4:4$,则$2S_{\triangle ABC} - S_{\triangle ABD} - S_{\triangle ACD} = $$\frac{1}{2}ab$.

答案：
11.$\frac{1}{2}ab$ 解：如图8−6，$\because BC = BD$，$\therefore \angle BDC = \angle BCD$(等边对等角)；又$\because \angle ABD:\angle BAC:\angle ACD:\angle CBD = 1:2:4:4$，$\therefore$设$\angle ABD = x$，则$\angle BAC = 2x$，$\angle ACD = 4x$，$\angle CBD = 4x$，$\therefore \angle ABD + \angle DBC + \angle BCD + \angle ACD + \angle BAC = x + 4x + \frac{180^{\circ}-4x}{2}+ 4x + 2x = 180^{\circ}$(三角形内角和定理)，解得，$x = 10^{\circ}$；$\therefore \angle ABD = 10^{\circ}$，$\angle CBD = \angle ACD = 40^{\circ}$，$\angle BCD = 70^{\circ}$；作点$D$关于$BC$的对称点$D'$，连接$BD'$，则$BD = BD'$，$\angle DBC = \angle D'BC = 40^{\circ}$，$\angle BCD' = \angle BCD = 70^{\circ}$，$\therefore \angle ABD' = \angle ABD + 2\angle DBC = 90^{\circ}$，$\angle ACD' = \angle ACD + 2\angle DBC = 180^{\circ}$，即点$D'$在$AC$的延长线上，$\therefore \triangle ABD'$是直角三角形；而$AB = a$，$BD = b$，$\therefore 2S_{\triangle ABC} - S_{\triangle ABD} - S_{\triangle BCD} = 2S_{\triangle ABC} - S_{\triangle ABD} - (S_{\triangle ABC} - S_{\triangle ABD} - S_{\triangle BCD}) = S_{\triangle ABC} + S_{\triangle BCD} = S_{\triangle ABC} + S_{\triangle BCD} = \frac{1}{2} · AB · BD' = \frac{1}{2} · AB · BD = \frac{1}{2}ab$. 故答案为$\frac{1}{2}ab$.
　　

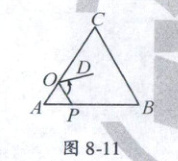
12. (湖北省鄂州高中自主招生)如图 8 - 11 所示,在等边$\triangle ABC$中,$AC = 9$,点$O$在$AC$上,且$AO = 3$,点$P$是$AB$上一动点,连接$OP$,将线段$OP$绕点$O$逆时针旋转$60^{\circ}$得到线段$OD$,要使点$D$恰好落在$BC$上,则$AP$的长为6.

答案：
12.6 提示：如图8−7，连接$PD$，$\because \angle POD = 60^{\circ}$，$OP = OD$，$\therefore \angle 1 + \angle 2 + 60^{\circ} = 180^{\circ}$，又$\angle 1 + \angle A + \angle APO = 180^{\circ}$，$\therefore \angle 2 = \angle APO$. 同理$\angle 1 = \angle CDO$，$\therefore \triangle APO \cong \triangle COD$，$\therefore AP = OC = AC - AO = 9 - 3 = 6$.
　　

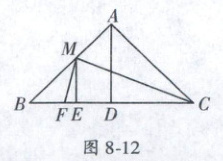
13. (衡阳县自主招生)如图 8 - 12,在$\triangle ABC$中,$AB = AC$,$CM$平分$\angle ACB$,与$AB$交于点$M$,$AD\perp BC$于点$D$,$ME\perp BC$于点$E$,$MF\perp MC$与$BC$交于点$F$,若$CF = 12$,则$DE = $3.

答案： 13.3 提示：取$CF$的中点$G$，连接$MG$，设$DE = x$，$EF = y$，可得$DC = CF - EF - DE = 12 - x - y$，$\because AB = AC$，$AD \perp BC$，$\therefore BD = DC = 12 - x - y$①，$\because FG = CG = 6$，$\therefore EG = FG - EF = 6 - y$②；$\because MG$是$Rt\triangle MFC$斜边上的中线，$\therefore \angle FGM = \angle BCM = \angle ACB$；$\because AB = AC$，$\therefore \angle B = \angle ACB$，$\therefore \angle FGM = \angle B$，又$ME \perp BG$，$BE = EG$，由①、②得$12 - 2x - y = 6 - y$，$\therefore x = 3$. 故答案为$3$.

14. 如图 8 - 13,图①是一块边长为 1,周长记为$P_1$的正三角形纸板,沿图①的底边剪去一块边长为$\frac{1}{2}$的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的$\frac{1}{2}$)后,得到图③,④…记第$n(n\geq 3)$块纸板的周长为$P_n$,则$P_n - P_{n - 1} = $$(\frac{1}{2})^{n - 1}$.(用含$n$的代数式表示)

答案： 14.$(\frac{1}{2})^{n - 1}$ 提示：由图可知，依次剪下小正三角形纸板过程中，原图形的两边分别是为$\frac{1}{4}$和$\frac{1}{2}$始终不变，当$n \geq 3$时，每一个纸板周长大于前一个纸板周长，如$P_3 - P_2 = (\frac{1}{4})^2$，$P_4 - P_3 = (\frac{1}{2})^3$，由此类推，$P_n - P_{n - 1} = (\frac{1}{2})^{n - 1}$.