2025年全国重点高中提前招生同步强化全真试卷八年级数学上册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年全国重点高中提前招生同步强化全真试卷八年级数学上册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
7. (马鞍山市第二中学实验班招生) 已知如图 7 - 7, $ D $ 为等边三角形 $ ABC $ 内一点, $ DB = DA$, $ BF = AB$, $\angle 1 = \angle 2$, 则 $\angle BFD$ 为 (
A.$15^{\circ}$
B.$20^{\circ}$
C.$30^{\circ}$
D.$45^{\circ}$
C
)
A.$15^{\circ}$
B.$20^{\circ}$
C.$30^{\circ}$
D.$45^{\circ}$
答案:
7.C 提示:连接CD,证△ACD≌△BCD。
8. (济南槐荫区期末) 如图 7 - 8, 在等边三角形 $ ABC $ 中, 在 $ AC $ 边上取两点 $ M$, $ N$, 使 $\angle MBN = 30^{\circ}$. 若 $ AM = m$, $ MN = x$, $ CN = n$, 则以 $ x$, $ m$, $ n $ 为边长的三角形的形状为 (
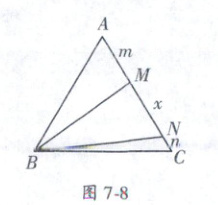
A.锐角三角形
B.直角三角形
C.钝角三角形
D.随 $ x$, $ m$, $ n $ 的值而定
C
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.随 $ x$, $ m$, $ n $ 的值而定
答案:
8.C 提示:如图7-4,将△ABM绕点B顺时针旋转60°得到△CBH,连接HN。
∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠A=60°,
∴∠MBN=30°,
∴∠ABM+∠CBH=30°,∠NBH=∠CBH+∠CBN=30°。
∵BM=BH,BN=BN,
∴△NBM≌△NBH,MN=NH=x。
∵x,m,n为边长的三角形△NCH是钝角三角形,故选C。

8.C 提示:如图7-4,将△ABM绕点B顺时针旋转60°得到△CBH,连接HN。
∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠A=60°,
∴∠MBN=30°,
∴∠ABM+∠CBH=30°,∠NBH=∠CBH+∠CBN=30°。
∵BM=BH,BN=BN,
∴△NBM≌△NBH,MN=NH=x。
∵x,m,n为边长的三角形△NCH是钝角三角形,故选C。

9. (2022 秋·武汉市洪山区期末) 如图 7 - 9, 已知 $\angle AOB = \alpha (0^{\circ} < \alpha < 60^{\circ})$, 射线 $ OA $ 上一点 $ M$, 以 $ OM$ 为边在 $ OA $ 下方作等边 $\triangle OMN$, 点 $ P $ 为射线 $ OB $ 上一点, 若 $\angle MNP = \alpha$, 则 $\angle OMP =$
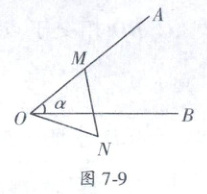
30°或120° - α
.
答案:
9.30°或120° - α 提示:

(1)当P位于MN左侧时,如图7-5图1,
∵△OMN是等边三角形,
∴MN=MO=ON,∠MON=∠MNO=60°。
∵∠MNP=∠AOB=α,
∴∠PON=∠PNO,
∴PO=PN,△MPO≌△MPN(SAS),
∴∠OMP=∠NMP=$\frac{1}{2}∠OMN=\frac{1}{2} × 60°=30°$。
(2)当P位于MN右侧时,如图7-5图2,将△MNP绕着点M顺时针旋转60°得到△MOQ,此时△MPQ是等边三角形,
∴∠MPQ=60°,
∴∠OMP=180°-∠MPQ-∠MOP=180°-60°-α=120°-α。
故答案为30°或120° - α。
9.30°或120° - α 提示:

(1)当P位于MN左侧时,如图7-5图1,
∵△OMN是等边三角形,
∴MN=MO=ON,∠MON=∠MNO=60°。
∵∠MNP=∠AOB=α,
∴∠PON=∠PNO,
∴PO=PN,△MPO≌△MPN(SAS),
∴∠OMP=∠NMP=$\frac{1}{2}∠OMN=\frac{1}{2} × 60°=30°$。
(2)当P位于MN右侧时,如图7-5图2,将△MNP绕着点M顺时针旋转60°得到△MOQ,此时△MPQ是等边三角形,
∴∠MPQ=60°,
∴∠OMP=180°-∠MPQ-∠MOP=180°-60°-α=120°-α。
故答案为30°或120° - α。
10. 如图 7 - 10, 在等边三角形 $ ABC $ 中, 点 $ D$, $ E $ 分别是 $ AB$, $ BC $ 边上的两个动点, 且满足 $ AD = BE$, $ AE $ 与 $ CD $ 交于点 $ F$, $ AG \perp CD $ 交于点 $ G$, 则 $\frac{FG}{AF} =$
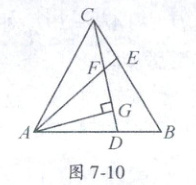
$\frac{1}{2}$
.
答案:
10.$\frac{FG}{AF}=\frac{1}{2}$ 提示:
∵CE=BD,∠ACE=∠B,AC=BC,
∴△ACE≌△CBD,
∴∠CAE=∠BCD。
∵∠ACF+∠BCD=60°,
∴∠CAE+∠ACF=60°,
∴∠AFG=60°。
又AG⊥CD,
∴$\frac{FG}{AF}=\frac{1}{2}$。
∵CE=BD,∠ACE=∠B,AC=BC,
∴△ACE≌△CBD,
∴∠CAE=∠BCD。
∵∠ACF+∠BCD=60°,
∴∠CAE+∠ACF=60°,
∴∠AFG=60°。
又AG⊥CD,
∴$\frac{FG}{AF}=\frac{1}{2}$。
11. (2022 秋·隰县期中) 如图 7 - 11, 已知: $\angle MON = 30^{\circ}$, 点 $ A_1$, $ A_2$, $ A_3$, … 在射线 $ OM $ 上, 点 $ B_1$, $ B_2$, $ B_3$, … 在射线 $ ON $ 上, $\triangle A_1B_1B_2$, $\triangle A_2B_2B_3$, $\triangle A_3B_3B_4$, … 均为等边三角形, 若 $ OB_1 = 1$, 则 $\triangle A_8B_8B_9$ 的边长为
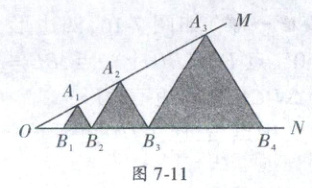
128
.
答案:
11.128 提示:设等边三角形的边长依次为$a_1$,$a_2$,$a_3$,⋯。
∵△$A_1B_1A_2$,$B_2A_2B_3$是等边三角形,如图7-6,
∵$B_1A_1=B_1A_2$,∠3=∠4=∠12=60°,
∴∠2=120°,∠MON=30°,
∴∠1=180°-120°-30°=30°。
又
∵∠3=60°,
∴∠5=180°-60°-30°=90°。
∵∠MON=∠1=30°,$OB_1=B_1A_1=1$,
∴$B_1A_1// A_2B_2// A_3B_3// A_4B_4// A_5B_5$,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴$a_2=2a_1$,$a_3=4a_1=4$,$a_4=8a_1=8$,$a_5=16a_1$,以此类推:$a_8=2^{7}=128$,即△$A_8B_8B_9$的边长为128,故答案为128。

11.128 提示:设等边三角形的边长依次为$a_1$,$a_2$,$a_3$,⋯。
∵△$A_1B_1A_2$,$B_2A_2B_3$是等边三角形,如图7-6,
∵$B_1A_1=B_1A_2$,∠3=∠4=∠12=60°,
∴∠2=120°,∠MON=30°,
∴∠1=180°-120°-30°=30°。
又
∵∠3=60°,
∴∠5=180°-60°-30°=90°。
∵∠MON=∠1=30°,$OB_1=B_1A_1=1$,
∴$B_1A_1// A_2B_2// A_3B_3// A_4B_4// A_5B_5$,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴$a_2=2a_1$,$a_3=4a_1=4$,$a_4=8a_1=8$,$a_5=16a_1$,以此类推:$a_8=2^{7}=128$,即△$A_8B_8B_9$的边长为128,故答案为128。

12. 如图 7 - 12, $\angle AOB = 60^{\circ}$, $ OA = OB$, 动点 $ C $ 从点 $ O $ 出发, 沿射线 $ OB $ 方向移动, 以 $ AC $ 为边在右侧作等边三角形 $ ACD$, 连接 $ AB$, $ BD$, 则 $ BD $ 所在的直线与 $ OA $ 所在的直线的位置关系是
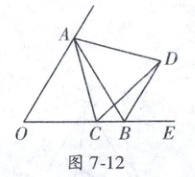
BD//OA
.
答案:
12.BD//OA 提示:
∵∠AOB=60°,OA=OB,
∴△OAB是等边三角形,
∴OA=AB,∠OAB=∠BOA=60°。
①当点C在线段OB上时,
∵△ACD是等边三角形,
∴AC=AD,∠CAD=60°,
∴∠OAC=∠BAD,可证△AOC≌△ABD(SAS),
∴∠ABD=∠AOC=60°,∠DBE=180°-∠ABO-∠ABD=60°=∠AOB,
∴BD//OA。
②当点C在OB的延长线上时,如图7-7,同①的方法得出OA//BD。
∵△ACD是等边三角形,
∴AC=AD,∠CAD=60°,
∴∠OAC=∠BAD,可证△AOC≌△ABD(SAS),
∴∠ABD=∠AOC=60°,
∴∠DBE=180°-∠ABO-∠ABD=60°=∠AOB,
∴BD//OA。
故答案为BD//OA。

12.BD//OA 提示:
∵∠AOB=60°,OA=OB,
∴△OAB是等边三角形,
∴OA=AB,∠OAB=∠BOA=60°。
①当点C在线段OB上时,
∵△ACD是等边三角形,
∴AC=AD,∠CAD=60°,
∴∠OAC=∠BAD,可证△AOC≌△ABD(SAS),
∴∠ABD=∠AOC=60°,∠DBE=180°-∠ABO-∠ABD=60°=∠AOB,
∴BD//OA。
②当点C在OB的延长线上时,如图7-7,同①的方法得出OA//BD。
∵△ACD是等边三角形,
∴AC=AD,∠CAD=60°,
∴∠OAC=∠BAD,可证△AOC≌△ABD(SAS),
∴∠ABD=∠AOC=60°,
∴∠DBE=180°-∠ABO-∠ABD=60°=∠AOB,
∴BD//OA。
故答案为BD//OA。

13. 如图 7 - 13, 在四边形 $ ABCD $ 中, $ AB = AC$, $\angle ABD = 60^{\circ}$, $\angle ADB = 76^{\circ}$, $\angle BDC = 28^{\circ}$, 则 $\angle DBC$ 的度数为
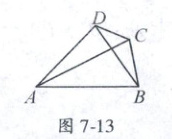
16°
.
答案:
13.16° 提示:如图7-8,延长BD到点E使DE=DC,连接AE,则易证△ADC≌△ADE(SAS),
∴∠DAC=∠EAD=76°-60°=16°,
∴∠BAC=44°-16°=28°,
∴∠DBC=(180°-28°)÷2-60°=16°。

13.16° 提示:如图7-8,延长BD到点E使DE=DC,连接AE,则易证△ADC≌△ADE(SAS),
∴∠DAC=∠EAD=76°-60°=16°,
∴∠BAC=44°-16°=28°,
∴∠DBC=(180°-28°)÷2-60°=16°。

14. (湖北省黄冈市八年级预赛) 如图 7 - 14. 点 $ P $ 是正 $\triangle ABC$ 内一点, $\angle APB = 125^{\circ}$, $\angle BPC = 100^{\circ}$, 则以 $ AP$, $ BP$, $ CP $ 为边组成的三角形各内角的度数为
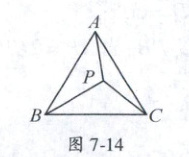
65°,75°,40°
.
答案:
14.65°,75°,40° 提示:如图7-9,以点A为中心,将△APB逆时针旋转60°,得△AQC,则△APB≌△AQC,
∴QC=PB,连接PQ,则△APQ为等边三角形,
∴PQ=PA,故△PCQ是以PA,PB,PC为边组成的三角形。
∵∠APB=∠AQC=125°,∠AQP=60°,
∴∠PQC=65°。
∠APC=360°-∠APB-∠BPC=135°,∠APQ=60°,
∴∠QPC=75°,于是∠PCQ=40°,故以PA,PB,PC为边组成的三角形三个内角是65°,75°,40°。

14.65°,75°,40° 提示:如图7-9,以点A为中心,将△APB逆时针旋转60°,得△AQC,则△APB≌△AQC,
∴QC=PB,连接PQ,则△APQ为等边三角形,
∴PQ=PA,故△PCQ是以PA,PB,PC为边组成的三角形。
∵∠APB=∠AQC=125°,∠AQP=60°,
∴∠PQC=65°。
∠APC=360°-∠APB-∠BPC=135°,∠APQ=60°,
∴∠QPC=75°,于是∠PCQ=40°,故以PA,PB,PC为边组成的三角形三个内角是65°,75°,40°。

15. (2023 秋·东丰县期末) 在 $\triangle DEF$ 中, $ DE = DF$, 点 $ B $ 在 $ EF $ 边上, 且 $\angle EBD = 60^{\circ}$, $ C $ 是射线 $ BD $ 上的一个动点 (不与点 $ B $ 重合, 且 $ BC \neq BE$), 在射线 $ BE $ 上截取 $ BA = BC$, 连接 $ AC$.
(1) 当点 $ C $ 在线段 $ BD $ 上时,
① 若点 $ C $ 与点 $ D $ 重合, 请根据题意补全图 1, 并直接写出线段 $ AE $ 与 $ BF $ 的数量关系为
② 如图 2, 若点 $ C $ 不与点 $ D $ 重合, 请证明 $ AE = BF + CD$;
八年级数学(上) · 26 ·
(2) 当点 $ C $ 在线段 $ BD $ 的延长线上时, 用等式表示线段 $ AE$, $ BF$, $ CD $ 之间的数量关系 (直接写出结果, 不需要证明).

(1) 当点 $ C $ 在线段 $ BD $ 上时,
① 若点 $ C $ 与点 $ D $ 重合, 请根据题意补全图 1, 并直接写出线段 $ AE $ 与 $ BF $ 的数量关系为
AE=BF
;② 如图 2, 若点 $ C $ 不与点 $ D $ 重合, 请证明 $ AE = BF + CD$;
八年级数学(上) · 26 ·
(2) 当点 $ C $ 在线段 $ BD $ 的延长线上时, 用等式表示线段 $ AE$, $ BF$, $ CD $ 之间的数量关系 (直接写出结果, 不需要证明).

答案:
15.解:
(1)①如图7-10图1,
∵BA=BC,∠EBD=60°,
∴△ABC是等边三角形,
∴AD=AB=BC,∠DAB=∠ABC=60°,∠EAD=∠FBD=120°。
∵DE=DF,∠E=∠F,可证△ADE≌△BDF(AAS),
∴AE=BF;故答案为AE=BF。
②证明:如图7-10图2,在BE上截取BG=BD,连接DG。
∵∠EBD=60°,BG=BD,
∴△GBD是等边三角形,同理△ABC也是等边三角形,
∴AG=CD,DE=DF,
∴∠E=∠F。
又
∵∠DGB=∠DBC=60°,
∴∠DGE=∠DBF=120°,可证△DGE≌△DBF(AAS),
∴GE=BF,
∴AE=BF + CD。
(2)如图7-10图4,连接DG,由
(1)知,GE=BF,AG=CD,
∴AE=EG - AG,
∴AE=CD - BF。


15.解:
(1)①如图7-10图1,
∵BA=BC,∠EBD=60°,
∴△ABC是等边三角形,
∴AD=AB=BC,∠DAB=∠ABC=60°,∠EAD=∠FBD=120°。
∵DE=DF,∠E=∠F,可证△ADE≌△BDF(AAS),
∴AE=BF;故答案为AE=BF。
②证明:如图7-10图2,在BE上截取BG=BD,连接DG。
∵∠EBD=60°,BG=BD,
∴△GBD是等边三角形,同理△ABC也是等边三角形,
∴AG=CD,DE=DF,
∴∠E=∠F。
又
∵∠DGB=∠DBC=60°,
∴∠DGE=∠DBF=120°,可证△DGE≌△DBF(AAS),
∴GE=BF,
∴AE=BF + CD。
(2)如图7-10图4,连接DG,由
(1)知,GE=BF,AG=CD,
∴AE=EG - AG,
∴AE=CD - BF。


查看更多完整答案,请扫码查看


