2025年全国重点高中提前招生同步强化全真试卷八年级数学上册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年全国重点高中提前招生同步强化全真试卷八年级数学上册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
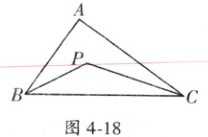
18. (2022·芜湖市无为实验中学竞赛)如图4-18,在△ABC中,∠ABC = 60°,∠ACB = 40°,P为∠ABC与∠ACB的平分线的交点,求证:AB = PC.

答案:
18.证明:如图4 - 11,连接AP并延长交BC于点D,作∠CAD的平分线AE,交BC于点E,
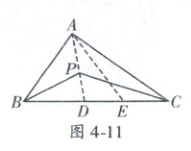
∴∠PAE=∠EAC;
∵P为∠ABC的平分线与∠ACB的平分线的交点,
∴∠BAD=∠DAC.
∵∠ABC=60°,∠ACB=40°,
∴∠BAC=80°.
∴∠BAD=$\frac{1}{2}$×80°=40°,∠EAD=20°,
∴∠BAE=60°,
∴△ABE为等边三角形,
∴AE=AB,
∴△ADE≌△CDP(ASA).
∴AE=PC,故AB=PC.
18.证明:如图4 - 11,连接AP并延长交BC于点D,作∠CAD的平分线AE,交BC于点E,

∴∠PAE=∠EAC;
∵P为∠ABC的平分线与∠ACB的平分线的交点,
∴∠BAD=∠DAC.
∵∠ABC=60°,∠ACB=40°,
∴∠BAC=80°.
∴∠BAD=$\frac{1}{2}$×80°=40°,∠EAD=20°,
∴∠BAE=60°,
∴△ABE为等边三角形,
∴AE=AB,
∴△ADE≌△CDP(ASA).
∴AE=PC,故AB=PC.
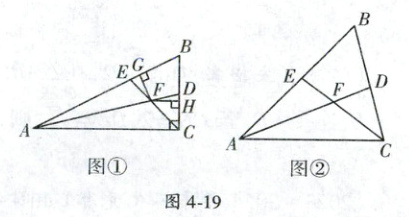
19. (2023秋·黄冈期末)如图①,在△ABC中,∠ACB是直角,∠B = 60°,AD,CE分别是∠BAC,∠BCA的平分线,AD,CE相交于点F,且FG⊥AB于G,FH⊥BC于H.
(1)求证:∠BEC = ∠ADC;
(2)请你判断FE与FD之间的数量关系,并证明;
(3)如图②,在△ABC中,如果∠ACB不是直角,∠B = 60°,AD,CE分别是∠BAC,∠BCA的平分线,AD,CE相交于点F.请问,你在(2)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
(1)求证:∠BEC = ∠ADC;
(2)请你判断FE与FD之间的数量关系,并证明;
(3)如图②,在△ABC中,如果∠ACB不是直角,∠B = 60°,AD,CE分别是∠BAC,∠BCA的平分线,AD,CE相交于点F.请问,你在(2)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

答案:
19.提示:
(1)
∵AD,CE分别是∠BAC,∠BCA的平分线,
∴∠DAC=∠DAB=$\frac{1}{2}$∠BAC=15°,∠ACE=$\frac{1}{2}$∠ACB=45°,
∴∠CDA=∠BAD+∠ABD=75°,∠BEC=∠BAC+∠ECA=75°,
∴∠BEC=∠ADC;
(2)相等 理由:连接BF,
∵F是角平分线交点,
∴BF也是角平分线,
∴HF=FG,∠DHF=∠EGF=90°.
∵在Rt△ABC中,∠ACB=90°,∠ABC=60°,
∴∠BAC=30°,
∴∠DAC=$\frac{1}{2}$∠BAC=15°,
∴∠CDA=75°.
∵∠HFC=45°,∠HFG=120°,
∴∠GFE=15°,
∴∠GEF=75°=∠HDF,
∴△DHF≌△EGF(AAS),
∴FE=FD;
(3)成立 理由:如图4 - 12,过点F作FM⊥BC于M.作FN⊥AB于N,连接BF,
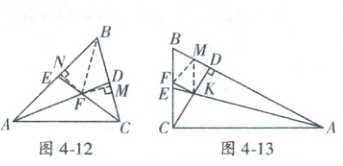
∵F是角平分线交点,
∴BF也是角平分线,
∴MF=FN,∠DMF=∠ENF=90°,
∴四边形BNFM是圆内接四边形.
∵∠ABC=60°,
∴∠MFN=180° - ∠ABC=120°.
∵∠CFA=180° - (∠FAC+∠FCA)=180° - $\frac{1}{2}$(∠ABC+∠ACB)=180° - $\frac{1}{2}$(180° - ∠ABC)=180° - $\frac{1}{2}$(180° - 60°)=120°,
∴∠DFE=∠CFA=∠MFN=120°.又
∵∠MFN=∠MFD+∠DFN,∠DFE=∠DFN+∠NFE,
∴∠DFM=∠NFE,
∴△DMF≌△ENF(ASA),
∴FE=FD.
19.提示:
(1)
∵AD,CE分别是∠BAC,∠BCA的平分线,
∴∠DAC=∠DAB=$\frac{1}{2}$∠BAC=15°,∠ACE=$\frac{1}{2}$∠ACB=45°,
∴∠CDA=∠BAD+∠ABD=75°,∠BEC=∠BAC+∠ECA=75°,
∴∠BEC=∠ADC;
(2)相等 理由:连接BF,
∵F是角平分线交点,
∴BF也是角平分线,
∴HF=FG,∠DHF=∠EGF=90°.
∵在Rt△ABC中,∠ACB=90°,∠ABC=60°,
∴∠BAC=30°,
∴∠DAC=$\frac{1}{2}$∠BAC=15°,
∴∠CDA=75°.
∵∠HFC=45°,∠HFG=120°,
∴∠GFE=15°,
∴∠GEF=75°=∠HDF,
∴△DHF≌△EGF(AAS),
∴FE=FD;
(3)成立 理由:如图4 - 12,过点F作FM⊥BC于M.作FN⊥AB于N,连接BF,

∵F是角平分线交点,
∴BF也是角平分线,
∴MF=FN,∠DMF=∠ENF=90°,
∴四边形BNFM是圆内接四边形.
∵∠ABC=60°,
∴∠MFN=180° - ∠ABC=120°.
∵∠CFA=180° - (∠FAC+∠FCA)=180° - $\frac{1}{2}$(∠ABC+∠ACB)=180° - $\frac{1}{2}$(180° - ∠ABC)=180° - $\frac{1}{2}$(180° - 60°)=120°,
∴∠DFE=∠CFA=∠MFN=120°.又
∵∠MFN=∠MFD+∠DFN,∠DFE=∠DFN+∠NFE,
∴∠DFM=∠NFE,
∴△DMF≌△ENF(ASA),
∴FE=FD.
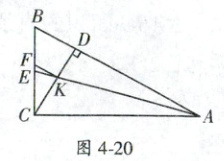
20. (大连市数学竞赛)如图4-20,在Rt△ABC中,∠ACB = 90°,CD⊥AB于点D,AE平分∠BAC,交CD于点K,交BC于点E,F是BE上的一点,且BF = CE,求证:FK//AB.

答案:
20.证明:如图4 - 13,过点K作KM//BC交AB于M,连接FM,则∠KMA=∠B.
∵AE平分∠BAC,
∴∠MAK=∠CAK,易证△AKC≌△AKM(AAS),
∴CK=MK.又
∵∠CEK=∠B+∠BAE,∠CKE=∠DCA+∠CAE,而∠B=∠DCA,∠BAE=∠CAE,
∴∠CEK=∠CKE,
∴CK=CE,
∴MK=CK=CE=BF.
∵KM//BC,
∴∠FMK=∠MFB,
∴△FMB≌△MFK(SAS),
∴∠BMF=∠KFM,
∴AB//FK.

20.证明:如图4 - 13,过点K作KM//BC交AB于M,连接FM,则∠KMA=∠B.
∵AE平分∠BAC,
∴∠MAK=∠CAK,易证△AKC≌△AKM(AAS),
∴CK=MK.又
∵∠CEK=∠B+∠BAE,∠CKE=∠DCA+∠CAE,而∠B=∠DCA,∠BAE=∠CAE,
∴∠CEK=∠CKE,
∴CK=CE,
∴MK=CK=CE=BF.
∵KM//BC,
∴∠FMK=∠MFB,
∴△FMB≌△MFK(SAS),
∴∠BMF=∠KFM,
∴AB//FK.

查看更多完整答案,请扫码查看


