2025年全国重点高中提前招生同步强化全真试卷八年级数学上册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年全国重点高中提前招生同步强化全真试卷八年级数学上册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
19. (2024·长沙市雅礼教育集团创新拔尖选拔赛)【基础巩固】(1)如图 1,在△ABC 与△ADE 中,AB = AC,AD = AE,∠BAC = ∠DAE,求证:△AEC≌△ADB.
【尝试应用】(2)如图 2,在△ABC 与△ADE 中,AB = AC,AD = AE,∠BAC = ∠DAE = 90°,B,D,E 三点在一条直线上,AC 与 BE 交于点 F,若点 F 为 AC 中点,
①求∠BEC 的大小;
②CE = 2,求△ACE 的面积.
【拓展提高】(3)如图 3,△ABC 与△ADE 中,AB = AC,DA = DE,∠BAC = ∠ADE = 90°,BE 与 CA 交于点 F,DC = DF,CD⊥DF,△BCF 的面积为 18,求 AF 的长.
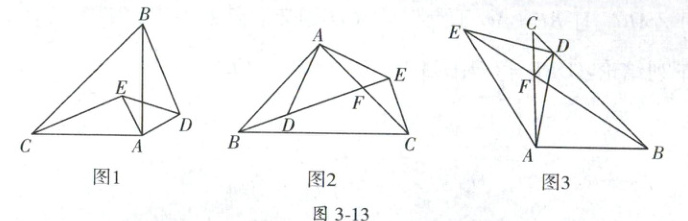
【尝试应用】(2)如图 2,在△ABC 与△ADE 中,AB = AC,AD = AE,∠BAC = ∠DAE = 90°,B,D,E 三点在一条直线上,AC 与 BE 交于点 F,若点 F 为 AC 中点,
①求∠BEC 的大小;
②CE = 2,求△ACE 的面积.
【拓展提高】(3)如图 3,△ABC 与△ADE 中,AB = AC,DA = DE,∠BAC = ∠ADE = 90°,BE 与 CA 交于点 F,DC = DF,CD⊥DF,△BCF 的面积为 18,求 AF 的长.

答案:
19.
(1)证明:
∵∠BAC = ∠DAE,
∴∠BAC - ∠BAE = ∠DAE - ∠BAE,即∠CAE = ∠BAD,
∴△AEC≌△ADB(SAS);
(2)解:①
∵AD = AE,∠DAE = 90°,
∴∠ADE = ∠AED = 45°,
∴∠ADB = 180° - ∠ADE = 180° - 45° = 135°.同
(1)得△AEC≌△ADB(SAS),
∴∠AEC = ∠ADB = 135°.
∴∠BEC = ∠AEC - ∠AED = 135° - 45° = 90°;②如图3 - 11图1,过点A作AG⊥DE于点G,则∠FGA = 90°,由①可知,∠FEC = 90°,
∴∠FGA = ∠FEC.
∵点F为AC中点,
∴AF = CF.又
∵∠AFG = ∠CFE,
∴△AGF≌△CEF(AAS),
∴AG = CE = 2,GF = EF.
∵AD = AE,∠DAE = 90°,
∴DG = EG = AG = 2,
∴GF = EF = $\frac{1}{2}$EG = 1,
∴$S_{\triangle ACE}$ = 2×$\frac{1}{2}$CE·EF = 2×$\frac{1}{2}$×2×1 = 2;
(3)解:如图3 - 11图2,连接CE,同
(2)得△CDE≌△FDA(SAS),
∴CE = AF,∠DCE = ∠DFA = 135°,
∴∠ACE = ∠DCE - ∠ACB = 135° - 45° = 90°,
∴△ACE≌△BAF(SAS),
∴$S_{\triangle ACE}$ = $S_{\triangle BAF}$.
∵∠ACE = ∠BAC,
∴CE//AB,
∴$S_{\triangle ABE}$ = $S_{\triangle ABC}$ = $\frac{1}{2}$AC·AB = $\frac{1}{2}$AC².
∵$S_{\triangle ABC}$ + $S_{\triangle ACE}$ - $S_{\triangle AEF}$ - $S_{\triangle CEF}$ = $S_{\triangle BCF}$,
∴$\frac{1}{2}$AC² + $\frac{1}{2}$AC·CE - $\frac{1}{2}$AC² - CE·CF = 18,
∴AC·AF - AF·CF = 36,
∴AF(AC - CF) = 36,
∴$AF^2$ = 36,
∴AF = $\sqrt{36}$ = 6.



19.
(1)证明:
∵∠BAC = ∠DAE,
∴∠BAC - ∠BAE = ∠DAE - ∠BAE,即∠CAE = ∠BAD,
∴△AEC≌△ADB(SAS);
(2)解:①
∵AD = AE,∠DAE = 90°,
∴∠ADE = ∠AED = 45°,
∴∠ADB = 180° - ∠ADE = 180° - 45° = 135°.同
(1)得△AEC≌△ADB(SAS),
∴∠AEC = ∠ADB = 135°.
∴∠BEC = ∠AEC - ∠AED = 135° - 45° = 90°;②如图3 - 11图1,过点A作AG⊥DE于点G,则∠FGA = 90°,由①可知,∠FEC = 90°,
∴∠FGA = ∠FEC.
∵点F为AC中点,
∴AF = CF.又
∵∠AFG = ∠CFE,
∴△AGF≌△CEF(AAS),
∴AG = CE = 2,GF = EF.
∵AD = AE,∠DAE = 90°,
∴DG = EG = AG = 2,
∴GF = EF = $\frac{1}{2}$EG = 1,
∴$S_{\triangle ACE}$ = 2×$\frac{1}{2}$CE·EF = 2×$\frac{1}{2}$×2×1 = 2;
(3)解:如图3 - 11图2,连接CE,同
(2)得△CDE≌△FDA(SAS),
∴CE = AF,∠DCE = ∠DFA = 135°,
∴∠ACE = ∠DCE - ∠ACB = 135° - 45° = 90°,
∴△ACE≌△BAF(SAS),
∴$S_{\triangle ACE}$ = $S_{\triangle BAF}$.
∵∠ACE = ∠BAC,
∴CE//AB,
∴$S_{\triangle ABE}$ = $S_{\triangle ABC}$ = $\frac{1}{2}$AC·AB = $\frac{1}{2}$AC².
∵$S_{\triangle ABC}$ + $S_{\triangle ACE}$ - $S_{\triangle AEF}$ - $S_{\triangle CEF}$ = $S_{\triangle BCF}$,
∴$\frac{1}{2}$AC² + $\frac{1}{2}$AC·CE - $\frac{1}{2}$AC² - CE·CF = 18,
∴AC·AF - AF·CF = 36,
∴AF(AC - CF) = 36,
∴$AF^2$ = 36,
∴AF = $\sqrt{36}$ = 6.




20. (2024·重庆)在△ABC 中,AB = AC,点 D 是 BC 边上一点(点 D 不与端点重合). 点 D 关于直线 AB 的对称点为 E,连接 AD,DE. 在直线 AD 上取一点 F,使∠EFD = ∠BAC,直线 EF 与直线 AC 交于点 G.
(1)如图 1,若∠BAC = 60°,BD < CD,∠BAD = α,求∠AGE 的度数(用含 α 的代数式表示);
(2)如图 1,若∠BAC = 60°,BD < CD,用等式表示线段 CG 与 DE 之间的数量关系,并证明;
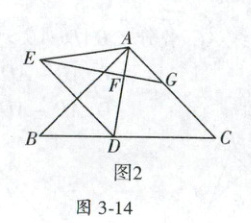
(3)如图 2,若∠BAC = 90°,点 D 从点 B 移动到点 C 的过程中,连接 AE,当△AEC 为等腰三角形时,请直接写出此时$\frac{CG}{AG}$的值.
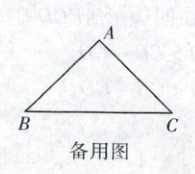
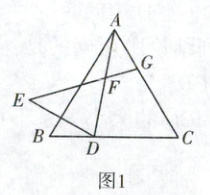
(1)如图 1,若∠BAC = 60°,BD < CD,∠BAD = α,求∠AGE 的度数(用含 α 的代数式表示);
(2)如图 1,若∠BAC = 60°,BD < CD,用等式表示线段 CG 与 DE 之间的数量关系,并证明;
(3)如图 2,若∠BAC = 90°,点 D 从点 B 移动到点 C 的过程中,连接 AE,当△AEC 为等腰三角形时,请直接写出此时$\frac{CG}{AG}$的值.



答案:
20.提示:
(1)设AB,EF交于H,
∵∠EFD = ∠BAC,∠BAC = 60°,
∴∠EFD = 60°.
∵∠EFD = ∠AHF + ∠BAD = ∠AHF + α,
∴∠AHF = 60° - α.
∵∠AGE + ∠AHF + ∠BAC = 180°,
∴∠AGE = 180° - 60° - ∠AHF = 120° - ∠AHF,
∴∠AGE = 120° - (60° - α) = 60° + α;

(2)CG = $\frac{2\sqrt{3}}{3}$DE,理由如下:如图3 - 12图1,在CG上截取CM = BD,连接BM,BE,AE,BM交AD于点Q,
∵AB = AC,∠BAC = 60°,
∴△BCA为等边三角形,
∴∠ABC = ∠C = 60°,BC = AB,
∴△ABD≌△BCM(SAS),
∴∠3 = ∠4.
∵∠AQM = ∠3 + ∠5,
∴∠AQM = ∠4 + ∠5 = 60°.
∵∠EFD = ∠BAC = 60°,
∴∠AQM = ∠EFD,
∴EG//BM.
∵点D关于直线AB的对称点为点E,
∴AE = AD,BE = BD,∠ABE = ∠ABC = 60°,
∴∠EBC = 120°,
∴∠EBC + ∠C = 180°,
∴EB//AC,
∴四边形EBMG是平行四边形,
∴BE = GM,
∴BE = GM = BD = CM,
∴CG = 2BD,记AB与DE的交点为点N,则由轴对称可知DE⊥AB
20.提示:
(1)设AB,EF交于H,
∵∠EFD = ∠BAC,∠BAC = 60°,
∴∠EFD = 60°.
∵∠EFD = ∠AHF + ∠BAD = ∠AHF + α,
∴∠AHF = 60° - α.
∵∠AGE + ∠AHF + ∠BAC = 180°,
∴∠AGE = 180° - 60° - ∠AHF = 120° - ∠AHF,
∴∠AGE = 120° - (60° - α) = 60° + α;

(2)CG = $\frac{2\sqrt{3}}{3}$DE,理由如下:如图3 - 12图1,在CG上截取CM = BD,连接BM,BE,AE,BM交AD于点Q,
∵AB = AC,∠BAC = 60°,
∴△BCA为等边三角形,
∴∠ABC = ∠C = 60°,BC = AB,
∴△ABD≌△BCM(SAS),
∴∠3 = ∠4.
∵∠AQM = ∠3 + ∠5,
∴∠AQM = ∠4 + ∠5 = 60°.
∵∠EFD = ∠BAC = 60°,
∴∠AQM = ∠EFD,
∴EG//BM.
∵点D关于直线AB的对称点为点E,
∴AE = AD,BE = BD,∠ABE = ∠ABC = 60°,
∴∠EBC = 120°,
∴∠EBC + ∠C = 180°,
∴EB//AC,
∴四边形EBMG是平行四边形,
∴BE = GM,
∴BE = GM = BD = CM,
∴CG = 2BD,记AB与DE的交点为点N,则由轴对称可知DE⊥AB
查看更多完整答案,请扫码查看


