《2025年全国重点高中提前招生同步强化全真试卷八年级数学上册》

18. (重庆市竞赛)如图6 - 14，△ABC是边长为1的等边三角形，△BDC是顶角∠BDC为120°的等腰三角形，以D为顶点作一个60°角，角的两边分别交AB于M，交AC于N，连接MN. 求证：△AMN的周长为2.

答案：
18.证明：如图6 - 13，在AC的延长线上截取CE = BM，可证Rt△BDM≌Rt△CDE。
得MD = ED，∠MDB = ∠EDC，
∴∠MDE = 120° - ∠MDB + ∠EDC = 120°，
又∠MDN = 60°，∠NDE = 60°，可证△MDN≌△EDN得MN = EN。
故△AMN的周长 = AM + MN + AN = AM + AN + NE = AM + AE = AB + AC = 2。

19. (天津市竞赛)如图6 - 15所示，在△ABC中，已知∠A = 90°，AB = AC，D为AC中点，AE⊥BD于点E，延长AE交BC于点F. 求证：∠ADB = ∠CDF.

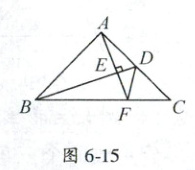
答案：
19.证明：如图6 - 14，作∠BAC的平分线与BD交于点G。
∵∠BAC = 90°，
∴∠3 = ∠DAG = $\frac{1}{2}$∠BAC = 45°。
∵AE⊥BD，
∴∠2 + ∠BAE = 90°，∠1 + ∠BAE = 90°，
∴∠1 = ∠2。
又
∵AB = AC，∠C = 45°，
∴△ABG≌△CAF，
∴AG = CF。
同理△ADG≌△CDF，故∠ADB = ∠CDF。

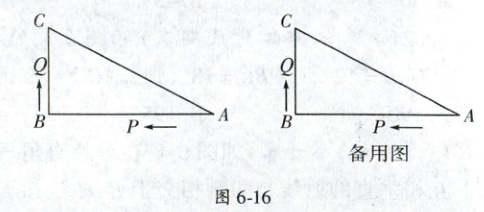
20. (2023秋·怀集县期末)如图6 - 16，在△ABC中，∠B = 90°，AB = 16 cm，BC = 12 cm，AC = 20 cm，P，Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1 cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2 cm，它们同时出发，设出发的时间为t s.
(1)BP =_(用t的代数式表示).
(2)当点Q在边BC上运动时，出发_s后，△PQB是等腰三角形.
(3)当点Q在边CA上运动时，出发几秒后，△BCQ是等腰三角形？

答案：
20.
(1)由题意可知AP = t，BQ = 2t，
∵AB = 16cm，
∴BP = AB - AP = (16 - t)cm。
(2)当点Q在边BC上运动，△PQB为等腰三角形时，则有BP = BQ，即16 - t = 2t，解得t = $\frac{16}{3}$。
∴出发$\frac{16}{3}$s后，△PQB能形成等腰三角形。
(3)
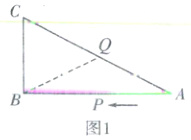
①当△BCQ是以BC为底边的等腰三角形时：CQ = BQ，如图6 - 15图1所示，则∠C = ∠CBQ。
∵∠ABC = 90°，
∴∠CBQ + ∠ABQ = 90°。
∵∠A + ∠C = 90°，
∴∠A = ∠ABQ，
∴BQ = AQ。
∴CQ = AQ = 10(cm)，
∴BC + CQ = 22(cm)，
∴t = 22÷2 = 11s。
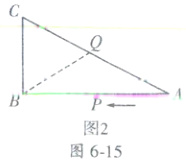
②当△BCQ是以BQ为底边的等腰三角形时：CQ = BC，如图6 - 15图2所示，则BC + CQ = 24(cm)，
∴t = 24÷2 = 12s。
③当△BCQ是以CQ为底边的等腰三角形时：BQ = BC，如图6 - 15图3所示。
∵$\frac{1}{2}$×AB×BC = $\frac{1}{2}$×AC×BD，
∴$\frac{1}{2}$×16×12 = $\frac{1}{2}$×20×BD，
∴BD = $\frac{48}{5}$。
∴CD = √(BC² - BD²) = $\frac{36}{5}$。
CQ = 2CD = $\frac{72}{5}$，
BC + CQ = 12 + $\frac{72}{5}$ = $\frac{132}{5}$，
t = $\frac{132}{5}$÷2 = $\frac{66}{5}$s。
综上所述；当t为11s或12s或$\frac{66}{5}$s时，△BCQ是等腰三角形。