《2025年全国重点高中提前招生同步强化全真试卷八年级数学上册》

11. (2024·广东省拔尖创新人才学科知识竞赛＜初赛＞) 五条长度均为整数厘米的线段: $ a_1,a_2,a_3,a_4,a_5 $, 满足 $ a_1 ＜ a_2 ＜ a_3 ＜ a_4 ＜ a_5 $, 其中 $ a_1 = 1 cm,a_5 = 9 cm $, 且这五条线段中的任意三条都不能构成三角形, 则 $ a_3 =$3$$ _ cm.

答案： 11.3　提示:解法一:根据三角形的三边关系，如果五条线段中的任意三条都不能构成三角形且五条长度均为整数厘米的线段，又a₁＜a₂＜a₃＜a₄＜a₅,则a₁≥2.要想使a₁,a₂,a₃构不成三角形,则a₃−a₂≥1,即a₃≥3;要想使a₃,a₄,a₅构不成三角形,则a₅−a₄≥a₃,即a₅≤a₄+a₃=6.若a₂,a₃,a₄构不成三角形,则a₂+a₃≤a₄,即a₄≤a₄−a₂=4,此时a₃=3或4,但当a₃=4时,没有任何一个整数能使a₁,a₄,a₅不能构成三角形,故排除.所以a₃=3.解法二:由题意,得a₁+a₂≤a₃,a₂+a₃≤a₄,a₃+a₄≤a₅,三个不等式相加得到a₁+2a₂+2a₃+a₄≤a₃+a₄+a₅,化简得到2a₂+a₃≤a₅−a₁=8,即2a₂+a₃≤8,
∵a₂≥2,
∴a₃只能取3或4.当a₃=4时,有a₂≤a₅−a₃=5,
∵a₅=5,a₂≤a₄−a₁=1,与a₂≥2矛盾;
∴a₃=3.

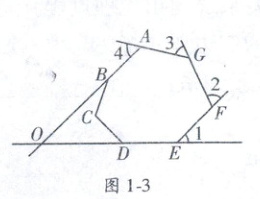
12. (2024·长沙市雅礼教育集团创新拔尖选拔赛) 如图 1 - 3, 七边形 $ ABCDEFG $ 中, $ AB,ED $ 的延长线交于点 $ O $, 外角 $ \angle 1,\angle 2,\angle 3,\angle 4 $ 的和等于 $ 220^{\circ} $, 则 $ \angle BOD $ 的度数是40°_ 度.

答案：
12.40°　提示:在DO延长线上找一点M,如图1−2.
∵多边形的外角和为360°,
∴∠BOM=360°−220°=140°.
∵∠BOD+∠BOM=180°,
∴∠BOD=180°−∠BOM=180°−140°=40°.

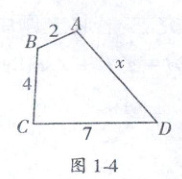
13. (2023 - 2024 学年合肥五十中培优选拔) 如图 1 - 4, $ ABCD $ 是凸四边形, 则 $ x $ 的取值范围是1＜x＜13_.

答案： 13.1＜x＜13　提示:连接BD,在△BCD中,
∵BC=4,CD=7,
∴7−4＜BD＜7+4,即3＜BD＜11;
∵BD−AB＜AD＜BD+AB,AB=2,
∴3−2＜AD＜11+2，即1＜AD＜13.
∴1＜x＜13.

14. (希望杯培训) 已知三角形的两角之和为 $ n^{\circ} $, 最大角比最小角大 $ 24^{\circ} $, 则 $ n $ 的取值范围为104°≤n°≤136°_.

答案： 14.104°≤n°≤136°　提示:设最小角为α°,则最大角为α°+24°,另一角为180°−2α°−24°=156°−2α°,依题意可得如下不等式组:
$\begin{cases}α°＞0° \\156°−2α°≥α° \\α°+24°≥156°−2α°\end{cases}$
解得44°≤α°≤52°.①若n°=180°−α°,则α°=180°−n°,
∴44°≤180°−n°≤52°,解得128°≤n°≤136°.②若n°=α°+(α°+24°)=2α°+24°,则α°=$\frac{1}{2}$(n°−24°),
∴44°≤$\frac{1}{2}$(n°−24°)≤52°,解得112°≤n°≤128°.③若n°=α°+(156°−2α°)=156°−α°,则α°=156°−n°,
∴44°≤156°−n°≤52°,解得104°≤n°≤112°.综上所述，n°的范围为104°≤n°≤136°.

15. (浙江自主招生) 如图 1 - 5, 设 $ P $ 为 $ \triangle ABC $ 外一点, 点 $ P $ 在边 $ AC $ 之外, 在 $ \angle B $ 之内. $ S_{\triangle PBC}:S_{\triangle PCA}:S_{\triangle PAB} = 4:2:3 $. 又知 $ \triangle ABC $ 三边 $ a,b,c $ 上的高为 $ h_a = 3,h_b = 5,h_c = 6 $, 求点 $ P $ 到三边的距离之和是多少.

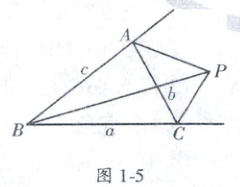
答案： 15.解:设P到三边的距离为Pₐ,P_b,P_c,S_{△PBC}=4S,S_{△PCA}=2S,S_{△PAB}=3S,则S_{△ABC}=S_{△PBC}+S_{△PAB}+S_{△PCA}=4S+3S+2S=5S,
∴$\frac{S_{△PBC}}{S_{△ABC}}=\frac{4S}{9S}=\frac{4}{9}=\frac{P_a}{h_a}$,
∴$P_a=\frac{4}{9}h_a$,同理可得$P_b=\frac{2}{9}h_b$,$P_c=\frac{3}{9}h_c$,$P_a+P_b+P_c=\frac{4}{9}h_a+\frac{2}{9}h_b+\frac{3}{9}h_c$.

16. (浙江余姚市自主招生) 在凸四边形 $ ABCD $ 中, $ \angle A - \angle B = \angle B - \angle C = \angle C - \angle D ＞ 0 $, 且四个内角中有一个角为 $ 84^{\circ} $, 求其余各角的度数.

答案： 16.提示:设∠A−∠B=∠B−∠C=∠C−∠D=x＞0,则∠A＞∠B＞∠C＞∠D,∠C=∠D+x,∠B=∠D+2x,∠A=∠D+3x.
∵∠A+∠B+∠C+∠D=6x+4∠D=360°,
∴∠D+$\frac{3}{2}$x=90°.①∠D=84°时,x=4°,∠A=96°,∠B=92°,∠C=88°;②∠C=84°时,2x+4∠C=360°,x=12°,∠A=108°,∠B=96°,∠D=72°;③∠B=84°时,−2x+4∠B=360°,x=−12°,∠A=72°,∠C=96°,∠D=108°(舍去);④∠A=84°时,−6x+4∠A=360°,x=−4°,∠D=96°,∠C=92°,∠B=88°(舍去).