《2025年全国重点高中提前招生同步强化全真试卷八年级数学上册》

9.(南靖县自主招生改编)某人在平面镜里看到的时间是12:01,此时实际时间是10:51.

答案： 9.10:51 提示:解:从镜子中看到的是12:01,则真实时间应该是将此读数倒看:10:51。故填10:51。

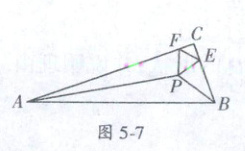
10.(2023·武汉江夏区月考)如图5-7,在$Rt\triangle ABC$中,$\angle C=90°$,两锐角的角平分线交于点$P$,点$E,F$分别在边$BC,AC$上,且都不与点$C$重合,若$\angle EPF=45°$,连接$EF$,当$AC=24$,$BC=7$,$AB=25$时,则$\triangle CEF$的周长为6.

答案：
10.6 解:如图5 - 8,过点P作PM⊥BC于M,PN⊥AC于N,PK⊥AB于K,在EB上取一点J,使得MJ = FN,连接PJ。
∵BP平分∠ABC,PA平分∠CAB,PM⊥BC,PN⊥AC,PK⊥AB,
∴PM = PK,PK = PN,
∴PM = PN,
∵∠C = ∠PMC = ∠PNC = 90°,
∴四边形PMCN是正方形,
∴CM = PM,
∴∠MPN = 90°,
∴△PMJ≌△PNF(SAS),
∴∠MPJ = ∠FPN,PJ = PF,
∴∠JPF = ∠MPN = 90°,
∵∠EPF = 45°,
∴∠EPF = ∠EPJ = 45°,
∴△PEF≌△PEJ(SAS),
∴EF = EJ,
∴EF = EM + FN,
∴△CEF的周长 = CE + EF + CF = CE + EM + CF + FN = 2CM = 2PM,
∵S△ABC = 1/2·BC·AC = 1/2(AC + BC + AB)·PM,
∴PM = 3,
∴△ECF的周长为6。

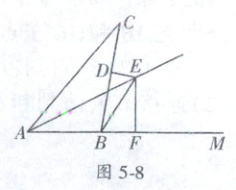
11.(2023秋·福建龙岩长仃六校联考)如图5-8,$AE$是$\angle CAM$的角平分线,点$B$在射线$AM$上,$DE$是线段$BC$的中垂线交$AE$于$E$,$EF\perp AM$.若$\angle ACB=26°$,$\angle CBE=25°$,则$\angle AED=$39°.

答案：
11.39° 解:如图5 - 9,连接CE,过E作ER⊥AC于R,交CD于Q,AE交BC于O,
∵DE是线段BC的中垂线,
∴∠EDC = 90°,CE = BE,
∴∠ECB = ∠CBE,
∵∠CBE = 25°,
∴∠ECB = 25°,
∴∠DEB = ∠CED = 90° - 25° = 65°,
∵ER⊥AC,ED⊥BC,
∴∠QRC = ∠QDE = 90°,
∴∠ACB + ∠CQR = 90°,∠EQD + ∠QED = 90°,
∴∠ACB = ∠QED,
∴∠QED = 26°,
∵AE平分∠CAM,ER⊥AC,EF⊥AM,
∴ER = EF,
∴Rt△ERCRt△EFB(HL),
∴∠EBF = ∠ACE = ∠ACB + ∠ECD = 26° + 25° = 51°,
∵∠EFB = 90°,
∴∠BEF = 90° - ∠EBF = 90° - 51° = 39°,∠REF = ∠RED + ∠BED + ∠BEF = 26° + 65° + 39° = 130°,
∵∠ARE = ∠AFE = 90°,
∴∠CAM = 360° - 90° - 90° - 130° = 50°,
∴∠CAE = 25°,
∴∠DOE = ∠CAE + ∠ACB = 51°,
∴∠AED = 90° - ∠DOE = 39°。

12.如图5-9,$\angle MON$内有一点$P,PP_1,PP_2$分别被$OM,ON$垂直平分,$P_1P_2$与$OM,ON$分别交于点$A,B$.若$P_1P_2=10\ cm$,则$\triangle PAB$的周长为10cm.

答案： 12.10cm 解:
∵P₁P₂分别被OM,ON垂直平分,
∴PA = AP₁,PB = BP₂;又
∵P₁P₂ = PA + AB + BP = PA + AB + PB = 10cm,
∴△PAB的周长为10cm。

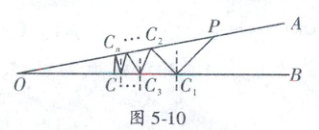
13.(广西竞赛)如图5-10,有两面夹角$\angle AOB=11°$的镜面$OA,OB$,从一个镜面上$P$点发射的光线,顺次在点$C_1,C_2,C_3,·s,C_n,C$反射,当垂直地射到镜面上的$C$点时,光线就会逆向从原路返回到$P$点,若当反射次数$n$为最大时,则$\angle OPC_1$的大小为2°度.

答案：
13.2° 解:如图5 - 10所示,CₙC₁⊥OB,∠AOB = 11°,∠OC₁C = 90° - 11° = 79°。根据反射定律易知∠Cₙ₋₂CₙCₙ₋₁ = ∠OC₁C = 79°,
∴∠CₙCₙ₋₁Cₙ₋₂ = 180° - 79°×2 = 22°。则∠CₙCₙ₋₁Cₙ₋₂ = 90° - 22° = 68°,可求得∠Cₙ₋₁Cₙ₋₂Cₙ₋₃ = 44°,同理∠Cₙ₋₁Cₙ₋₂Cₙ₋₃ = 66°,…,∠C₃C₂C₁ = 132°,∠C₁C₂P = 154°,∠APC₁ = 176°,
∵入射角此时已不能再大,
∴∠OPC₁ = (180° - 176°)÷2 = 2°

14.(山东省竞赛)如图5-11,在$Rt\triangle ABC$中,$\angle ACB=90°$,$\angle CAB=30°$,$\angle ACB$的平分线与$\angle ABC$的外角平分线交于点$E$,连接$AE$,则$\angle AEB=$45°.

答案：
14.45° 提示:如图5 - 11,过点E分别作EF⊥AC于点F,EG⊥AB于点G,EM⊥BC于点M。可知EG = EM = EF,
∴AE平分∠BAF,
∴∠1 = 1/2·∠BAF = 75°,∠2 = 1/2∠ABM = 60°,可得∠AEB = 45°

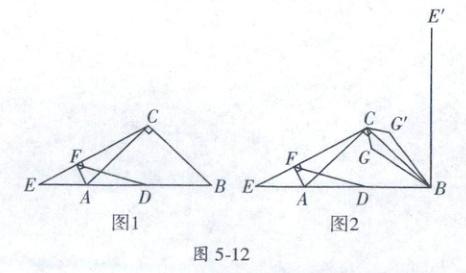
15.(2024·重庆市江津区月考)如图1,在等腰直角三角形$ABC$中,$AB=4\sqrt{2}$,点$D$是斜边$AB$的中点,点$E$是$BA$延长线上一点,连接$CE$,过点$A$作$AF\perp CE$于点$F$,连接$DF$.
(1)当$\angle AEC=30°$时,求$EF$的长;
(2)求证:$AF+CF=\sqrt{2}DF$;
(3)如图2,点$G$为平面内一点,且$CG=1$,连接$BG$,将$\triangle BCG$沿直线$BC$翻折得到$\triangle BCG'$,将线段$BE$绕点$B$顺时针旋转$90°$得到线段$BE'$,当点$E$在射线$BA$上运动时,请直接写出$E'G'$的最小值.

答案：
15.
(1)解:连接CD,
∵等腰Rt△ABC中,AB = 4√2,点D是斜边AB的中点,
∴CD = AD = DB = 1/2AB = 1/2×4√2 = 2√2,
∵∠AEC = 30°,ED = √3CD = √3×2√2 = 2√6,
∴EA = ED - AD = 2√6 - 2√2,
∴EF = √3/2EA = √3/2(2√6 - 2√2) = 3√2 - √6。
(2)证明:如图5 - 12图1,过点B,作BG⊥EC,交EC的延长线于点G,连接DG,
∴∠GCB + ∠GBC = 90°,
∵AC⊥BC,
∴∠GCB + ∠FCA = 90°,
∴∠GBC = ∠FCA,又
∵AC = BC,
∴△FAC≌△GCB(AAS),
∴AF = CG,
∵∠FAD = ∠GCD = 120°,AD = CD,
∴△FAD≌△GCD(SAS),
∴FD = DG,∠ADF = ∠CDG,
∴∠ADF + ∠FDC = ∠CDG + ∠FDC = 90°,即∠FDG = 90°,
∴△FDG是等腰直角三角形,
∴FG = √2FD,即CG + CF = √2FD,
∴AF + CF = √2DF。
(3)解:如图5 - 12图2,由翻折的性质可得,CG = CC' = 1,当CE'⊥BE',点G'在线段CE'上,E'G'取得最小值,
∵CD⊥BD,BD⊥BE',
∴CE' = BD = 2√2,E'G' = CE' - CG' = 2√2 - 1。