2025年全国重点高中提前招生同步强化全真试卷八年级数学上册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年全国重点高中提前招生同步强化全真试卷八年级数学上册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
8. (浙江自主招生)如图 3 - 5,在△ABC 中,AD 是∠A 的外角平分线,P 是 AD 上异于 A 的任意一点,设 PB = m,PC = n,AB = c,AC = b,则(m + n)与(b + c)的大小关系是 (
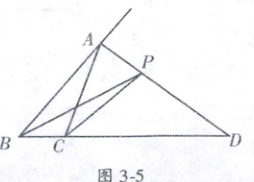
A.m + n > b + c
B.m + n < b + c
C.m + n = b + c
D.无法确定
A
)
A.m + n > b + c
B.m + n < b + c
C.m + n = b + c
D.无法确定
答案:
8.A 提示:在BA的延长线上取点E,使AE = AC,连接EP,如图3 - 3.
∵AD是∠BAC的外角平分线,∠CAD = ∠EAD,可证△ACP≌△AEP(SAS),
∴PE = PC.在△PBE中,PB + PE>AB + AE,
∵PB = m,PC = n,AB = c,AC = b,
∴m + n>b + c.
∵AD是∠BAC的外角平分线,∠CAD = ∠EAD,可证△ACP≌△AEP(SAS),
∴PE = PC.在△PBE中,PB + PE>AB + AE,
∵PB = m,PC = n,AB = c,AC = b,
∴m + n>b + c.
9. (福州一中自主招生)如图 3 - 6,线段 AB,CD 相交于点 O,∠DAB 和∠BCD 的平分线 AP 和 CP 相交于点 P,若∠D = 70°,∠B = 20°,则∠P 的度数为
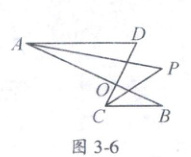
45°
.
答案:
9.45° 提示:由对顶三角形的性质知∠DAP + ∠D = ∠PCD + ∠P①,∠PCB + ∠B = ∠PAB + ∠P②,① + ②得∠DAP + ∠D + ∠PCB + ∠B = ∠PCD + ∠PAB + 2∠P,
∵∠DAP = ∠PAB,∠PCB = ∠PCD,
∴∠D + ∠B = 2∠P,
∴∠P = $\frac{1}{2}$(∠B + ∠D) = $\frac{1}{2} × (20° + 70°)$ = 45°.
∵∠DAP = ∠PAB,∠PCB = ∠PCD,
∴∠D + ∠B = 2∠P,
∴∠P = $\frac{1}{2}$(∠B + ∠D) = $\frac{1}{2} × (20° + 70°)$ = 45°.
10. (陕西西安自主招生)如图 3 - 7,已知∠BAD = ∠DAC = 9°,AD⊥AE,且 AB + AC = BE. 则∠B =
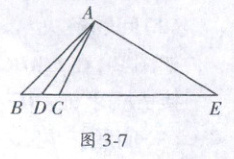
48°
.
答案:
10.48° 提示:延长BA到F,使AF = AC,连接EF,如图3 - 4所示:
∵AB + AC = BE,
∴AB + AF = BE,即BF = BE,
∴∠F = ∠BEF = $\frac{180° - ∠B}{2}$.
∵∠BAD = ∠DAC = 9°,AD⊥AE,即∠DAE = 90°,
∴∠FAE = 180° - (∠BAD + ∠DAE) = 180° - (9° + 90°) = 81°,∠CAE = ∠DAE - ∠DAC = 90° - 9° = 81°,
∴∠FAE = ∠CAE,
∴△AFE≌△ACE(SAS),
∴∠F = ∠ACE.又
∵∠ACE为△ABC的外角,
∴∠ACE = ∠B + ∠BAC = ∠B + 18°,
∴∠F = ∠B + 18°,
∴∠B + 18° = $\frac{180° - ∠B}{2}$,解得∠B = 48°.
∵AB + AC = BE,
∴AB + AF = BE,即BF = BE,
∴∠F = ∠BEF = $\frac{180° - ∠B}{2}$.
∵∠BAD = ∠DAC = 9°,AD⊥AE,即∠DAE = 90°,
∴∠FAE = 180° - (∠BAD + ∠DAE) = 180° - (9° + 90°) = 81°,∠CAE = ∠DAE - ∠DAC = 90° - 9° = 81°,
∴∠FAE = ∠CAE,
∴△AFE≌△ACE(SAS),
∴∠F = ∠ACE.又
∵∠ACE为△ABC的外角,
∴∠ACE = ∠B + ∠BAC = ∠B + 18°,
∴∠F = ∠B + 18°,
∴∠B + 18° = $\frac{180° - ∠B}{2}$,解得∠B = 48°.
11. (“希望杯”初二)若△ABC 的三个内角满足 3∠A > 5∠B,3∠C > 2∠B,则△ABC 必是
钝角
三角形. (选填“锐角”“直角”或“钝角”)
答案:
11.钝角 提示:
∵∠A + ∠B + ∠C = 180°,
∴∠C = 180° - ∠A - ∠B,又3∠C<2∠B,
∴3(180° - ∠A - ∠B)<2∠B,即540° - 3∠A<5∠B,
∴∠B>$\frac{540 - 3∠A}{5}$,
∵3∠A>5∠B,∠B<$\frac{3}{5}$∠A,
∴$\frac{540° - 3∠A}{5}$<$\frac{3}{5}$∠A,
∴540° - 3∠A<3∠A,
∴∠A>90°.
∵∠A + ∠B + ∠C = 180°,
∴∠C = 180° - ∠A - ∠B,又3∠C<2∠B,
∴3(180° - ∠A - ∠B)<2∠B,即540° - 3∠A<5∠B,
∴∠B>$\frac{540 - 3∠A}{5}$,
∵3∠A>5∠B,∠B<$\frac{3}{5}$∠A,
∴$\frac{540° - 3∠A}{5}$<$\frac{3}{5}$∠A,
∴540° - 3∠A<3∠A,
∴∠A>90°.
12. (江西婺源县重点高中自主招生)以线段 AC 为对角线的四边形 ABCD(它的四个顶点 A,B,C,D 按顺时针方向排列),已知 AB = BC = CD,∠ABC = 100°,∠CAD = 40°,则∠BCD 的度数为
80°或100°
.
答案:
12.80°或100° 提示:
∵AB = BC,∠ABC = 100°,
∴∠1 = ∠2 = ∠CAD = 40°,
∴AD//BC.点D的位置有两种情况:
(1)如图3 - 5①,过点C分别作CE⊥AB于E,CF⊥AD于F,
∵∠1 = ∠CAD,CE = CF,
∴Rt△ACE≌Rt△ACF,
∴∠ACE = ∠ACF;同理可证Rt△BCE≌Rt△DCF,
∴∠BCE = ∠DCF,
∴∠ACD = ∠2 = 40°,
∴∠BCD = 80°;
(2)如图3 - 5②,
∵AD'//BC,AB = CD',
∴四边形ABCD'是等腰梯形,
∴∠BCD' = ∠ABC = 100°.综上所述,∠BCD = 80°或100°.
∵AB = BC,∠ABC = 100°,
∴∠1 = ∠2 = ∠CAD = 40°,
∴AD//BC.点D的位置有两种情况:
(1)如图3 - 5①,过点C分别作CE⊥AB于E,CF⊥AD于F,
∵∠1 = ∠CAD,CE = CF,
∴Rt△ACE≌Rt△ACF,
∴∠ACE = ∠ACF;同理可证Rt△BCE≌Rt△DCF,
∴∠BCE = ∠DCF,
∴∠ACD = ∠2 = 40°,
∴∠BCD = 80°;
(2)如图3 - 5②,
∵AD'//BC,AB = CD',
∴四边形ABCD'是等腰梯形,
∴∠BCD' = ∠ABC = 100°.综上所述,∠BCD = 80°或100°.
13. (2024·肥城市一模)一张正方形纸的内部被针扎了 2010 个孔,这些孔和正方形的顶点之中的任何 3 点都不共线. 作若干条互不相交的线段,它们的端点都是这些孔或正方形的顶点,这些线段将正方形分割成一些三角形,并且在这些三角形的内部和边上都不再有小孔. 请问一共作了
6031
条线段. 共得到4022
个三角形.
答案:
13.6031 4022 提示:把2010个小孔和正方形的4个顶点所组成的集合称之为M,显然,M中的点都是一些三角形的公共顶点,下面我们从两个方面来计算所有三角形的内角和,①设共分成了n个三角形,于是它们的内角和为n·180°;②另一方面,这些三角形的内角的顶点都是M中的点,也即它们的内角都是由M中的点提供的,正方形的每个顶点都提供90°的角,每个孔点则提供360°的角,所以得到的n个三角形的内角和又应为4×90° + 2010×360° = 2011×360°,综合两个方面可得n·180° = 2011×360°,则n = 4022,即有4022个三角形,这4022个三角形共有4022×3条边,其中有4条边是原正方形的4条边,不用另行作出,其他各边都是作出的线段,每条线段恰为两个三角形的公共边,故作出的线段总数为(4022×3 - 4)÷2 = 6031.综上所述可得一共作了6031条线段,共得到4022个三角形.
14. (2024·重庆南岸区自主招生)如图 3 - 8,正五边形 ABCDE 中,M,N 分别是 CD,DE 的中点,连接 AM,BN 相交于点 O,那么∠AOB 的度数为
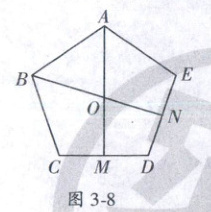
72°
.
答案:
14.提示:如图3 - 6,
∵五边形ABCDE是正五边形,
∴BC = DE,∠BCM = ∠EDM = 108°.
∵M是CD的中点,
∴CM = DM,
∴△BCM≌△EDM(SAS).
∴BM = EM.
∵AB = AE,
∴AM垂直平分BE,
∴∠OBH + ∠BOH = 90°,则△BCD≌△BAE(SAS),
∴BD = BE,
∵N是DE的中点,
∴BN⊥DE,
∴∠EBN + ∠BEN = 90°,
∵∠BAE = 108°,AB = AE,
∴∠AEB = ∠ABE = 36°,
∴∠BEN = 108° - 36° = 72°,
∴∠BOA = ∠BEN = 72°,故答案为72°.
14.提示:如图3 - 6,
∵五边形ABCDE是正五边形,
∴BC = DE,∠BCM = ∠EDM = 108°.
∵M是CD的中点,
∴CM = DM,
∴△BCM≌△EDM(SAS).
∴BM = EM.
∵AB = AE,
∴AM垂直平分BE,
∴∠OBH + ∠BOH = 90°,则△BCD≌△BAE(SAS),
∴BD = BE,
∵N是DE的中点,
∴BN⊥DE,
∴∠EBN + ∠BEN = 90°,
∵∠BAE = 108°,AB = AE,
∴∠AEB = ∠ABE = 36°,
∴∠BEN = 108° - 36° = 72°,
∴∠BOA = ∠BEN = 72°,故答案为72°.

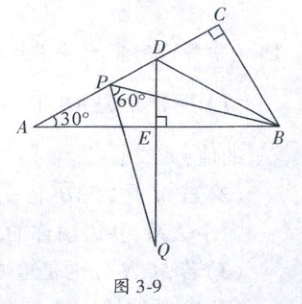
15. (深圳市“鹏程杯”八年级邀请赛)如图 3 - 9,在 Rt△ABC 中,∠ACB = 90°,∠A = 30°,BD 是△ABC 的角平分线,DE⊥AB 于点 E. 在线段 AD 上任取一点 P,以 PB 为一边,在 PB 的下方作∠BPQ = 60°,PQ 交 DE 延长线于点 Q. 请判断线段 DA,DP,DQ 之间的数量关系,并证明你的结论.

答案:
15.解:DQ = DP + DA,理由如下:如图3 - 7,以PD为边作等边三角形PDF,
∴PD = FD = PF,∠PFD = ∠PDF = ∠DPF = 60°,
∵∠ACB = 90°,∠A = 30°,
∴∠ABC = 60°,
∵BD是△ABC的角平分线,
∴∠ABD = ∠CBD = 30° = ∠A,
∴∠ADB = 120°,AD = BD,
∴∠ADB + ∠ADF = 180°,点B,点D,点F三点共线.
∵DE⊥AB,AD = BD,
∴∠ADE = ∠BDE = 60°,
∴∠PFB = ∠PDQ.
∵∠FPD = ∠BPQ = 60°,
∴∠BPF = ∠QPD,可得△BPF≌△QPD(ASA),BF = DQ,DQ = BF = DP + DB = DP + DA.
15.解:DQ = DP + DA,理由如下:如图3 - 7,以PD为边作等边三角形PDF,
∴PD = FD = PF,∠PFD = ∠PDF = ∠DPF = 60°,
∵∠ACB = 90°,∠A = 30°,
∴∠ABC = 60°,
∵BD是△ABC的角平分线,
∴∠ABD = ∠CBD = 30° = ∠A,
∴∠ADB = 120°,AD = BD,
∴∠ADB + ∠ADF = 180°,点B,点D,点F三点共线.
∵DE⊥AB,AD = BD,
∴∠ADE = ∠BDE = 60°,
∴∠PFB = ∠PDQ.
∵∠FPD = ∠BPQ = 60°,
∴∠BPF = ∠QPD,可得△BPF≌△QPD(ASA),BF = DQ,DQ = BF = DP + DB = DP + DA.

16. (北京市竞赛)如图 3 - 10,在△ABC 中,∠ABC = 46°,点 D 是边 BC 上的一点,DC = AB,∠DAB = 21°,试确定∠CAD 的度数.


答案:
16.解:如图3 - 8,作△ABD关于AD的轴对称图形△AED,即将△ABD沿AD翻折至△ADE,连接CE,则∠EAD = 21°,AE = AB,
∴DE = BD,∠ADC = 21° + 46° = 67°,故∠ADE = ∠ADB = 180° - 67° = 113°.∠CDE = 113° - 67° = 46°,
∵DC = AB,
∴△CDE≌△ABD≌△AED,设O为AE与DC的交点,
∵∠ODE = ∠OED = 46°,
∴OD = OE,又DC = AE,则AO = CO,从而∠OCA = ∠OAC,故∠COE = 2∠ACO,易知∠COE = 2×46° = 92°,从而∠ACO = 46° = ∠OAC,得∠CAD = ∠DAE + ∠OAC = 67°.
16.解:如图3 - 8,作△ABD关于AD的轴对称图形△AED,即将△ABD沿AD翻折至△ADE,连接CE,则∠EAD = 21°,AE = AB,
∴DE = BD,∠ADC = 21° + 46° = 67°,故∠ADE = ∠ADB = 180° - 67° = 113°.∠CDE = 113° - 67° = 46°,
∵DC = AB,
∴△CDE≌△ABD≌△AED,设O为AE与DC的交点,
∵∠ODE = ∠OED = 46°,
∴OD = OE,又DC = AE,则AO = CO,从而∠OCA = ∠OAC,故∠COE = 2∠ACO,易知∠COE = 2×46° = 92°,从而∠ACO = 46° = ∠OAC,得∠CAD = ∠DAE + ∠OAC = 67°.

查看更多完整答案,请扫码查看


