第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
9. 小林在计算 2.47 加一个一位小数时,由于错误地把数的末位对齐,结果得到 2.9,正确的得数是(
6.7
)。
答案:
2.9 - 2.47 = 0.43
0.43 × 10 = 4.3
2.47 + 4.3 = 6.7
6.7
0.43 × 10 = 4.3
2.47 + 4.3 = 6.7
6.7
10. 火星与太阳的平均距离约是 227940000 千米,改写成用“亿千米”作单位的数是(
2.2794
)亿千米,保留两位小数约是(2.28
)亿千米。
答案:
2.2794;2.28。
11. 一个四位小数精确到百分位后是 6.74,这个四位小数最大是(
6.7449
),最小是(6.7350
)。
答案:
答题卡:
11.
最大四位小数:6.7449(四舍五入到百分位为6.74,且为最大值,因此千分位取4,万分位取最大值9)
但由于四位小数只需考虑到万分位,且要使得整个数尽可能大但不超过6.74的精确范围,所以最大为6.7449中的9可省略,即最大为6.744(因为当千分位为4时,百分位不加1,为最大精确值)
但根据常规四舍五入理解,我们取到能四舍五入后仍为6.74的最大值,即6.744(万分位为最大数9时仍四舍五入为6.74,但通常我们保留到需要精确的下一位,所以写6.744即可)
最终最大值为:6.744
最小四位小数:6.7350(四舍五入到百分位为6.74,且为最小值,因此千分位取5,万分位取最小值0,但因为是小数,所以末尾0可省略)
简化后最小为:6.735
综上,这个四位小数最大是 6.744,最小是 6.735。
11.
最大四位小数:6.7449(四舍五入到百分位为6.74,且为最大值,因此千分位取4,万分位取最大值9)
但由于四位小数只需考虑到万分位,且要使得整个数尽可能大但不超过6.74的精确范围,所以最大为6.7449中的9可省略,即最大为6.744(因为当千分位为4时,百分位不加1,为最大精确值)
但根据常规四舍五入理解,我们取到能四舍五入后仍为6.74的最大值,即6.744(万分位为最大数9时仍四舍五入为6.74,但通常我们保留到需要精确的下一位,所以写6.744即可)
最终最大值为:6.744
最小四位小数:6.7350(四舍五入到百分位为6.74,且为最小值,因此千分位取5,万分位取最小值0,但因为是小数,所以末尾0可省略)
简化后最小为:6.735
综上,这个四位小数最大是 6.744,最小是 6.735。
12. 飞飞在玩拼图游戏,按如图所示的方法继续拼下去,4 个这样的图形拼成的总长度是(
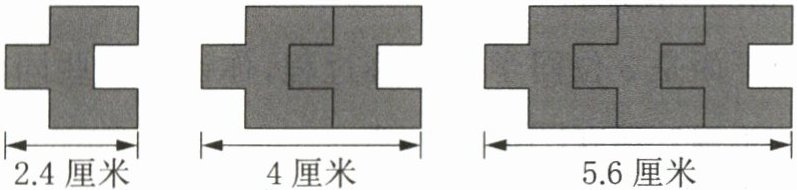
7.2
)厘米,5 个这样的图形拼成的总长度是(8.8
)厘米。
答案:
设拼$n$个图形时的总长度为$a_{n}$厘米。
$a_{1}=2.4$;
$a_{2}=4=2.4+(4 - 2.4)=2.4 + 1.6$;
$a_{3}=5.6=4+(5.6 - 4)=2.4+1.6×2$。
由此可推出$a_{n}=2.4 + 1.6×(n - 1)$,化简可得$a_{n}=1.6n + 0.8$。
当$n = 4$时,$a_{4}=1.6×4+0.8=6.4 + 0.8 = 7.2$(厘米)。
当$n = 5$时,$a_{5}=1.6×5+0.8=8 + 0.8 = 8.8$(厘米)。
故答案为:$7.2$;$8.8$。
$a_{1}=2.4$;
$a_{2}=4=2.4+(4 - 2.4)=2.4 + 1.6$;
$a_{3}=5.6=4+(5.6 - 4)=2.4+1.6×2$。
由此可推出$a_{n}=2.4 + 1.6×(n - 1)$,化简可得$a_{n}=1.6n + 0.8$。
当$n = 4$时,$a_{4}=1.6×4+0.8=6.4 + 0.8 = 7.2$(厘米)。
当$n = 5$时,$a_{5}=1.6×5+0.8=8 + 0.8 = 8.8$(厘米)。
故答案为:$7.2$;$8.8$。
1. 两数相减得 0.28,被减数是 8.36,减数是(
A.8.08
B.8.18
C.8.64
A
)。A.8.08
B.8.18
C.8.64
答案:
答题卡:
1. 解:根据被减数 - 减数 = 差,可得减数 = 被减数 - 差。
已知被减数是 8.36,差是 0.28,则减数为 8.36 - 0.28 = 8.08。
答案选 A。
1. 解:根据被减数 - 减数 = 差,可得减数 = 被减数 - 差。
已知被减数是 8.36,差是 0.28,则减数为 8.36 - 0.28 = 8.08。
答案选 A。
2. 下面的数与 1 最接近的是(
A.0.999
B.1.01
C.0.9998
C
)。A.0.999
B.1.01
C.0.9998
答案:
A选项与1的差:
|1 - 0.999| = 0.001
B选项与1的差:
|1.01 - 1| = 0.01
C选项与1的差:
|1 - 0.9998| = 0.0002
比较得:
0.0002 < 0.001 < 0.01
答:选C。
|1 - 0.999| = 0.001
B选项与1的差:
|1.01 - 1| = 0.01
C选项与1的差:
|1 - 0.9998| = 0.0002
比较得:
0.0002 < 0.001 < 0.01
答:选C。
3. 在如图所示的框中,百分位不够减,需要向“5”借“1”,这个“1”表示(
A.10 个 0.1
B.10 个 0.01
C.10 个 0.001
B
)。
A.10 个 0.1
B.10 个 0.01
C.10 个 0.001
答案:
百分位不够减,向十分位借“1”,这里的“1”在十分位上,表示 1 个 0.1,借到百分位后,1 个 0.1 就是 10 个 0.01。
答案选B。
答案选B。
4. 一个加数是两位数,另一个加数是三位小数,它们的和是(
A.一
B.二
C.三
C
)位小数。A.一
B.二
C.三
答案:
答题卡:
4. C
解析:
一个加数是两位数(整数部分,无小数),另一个加数是三位小数。
根据小数加法规则,和的小数位数与小数部分位数最多的加数一致。
因此,和是三位小数。
答案选C。
4. C
解析:
一个加数是两位数(整数部分,无小数),另一个加数是三位小数。
根据小数加法规则,和的小数位数与小数部分位数最多的加数一致。
因此,和是三位小数。
答案选C。
5. 在一道减法算式中,差是 5.28,如果被减数不变,减数减少 0.8,那么现在的差是(
A.4.48
B.6.08
C.5.2
B
)。A.4.48
B.6.08
C.5.2
答案:
B.6.08
查看更多完整答案,请扫码查看


