2025年复习大本营期末假期复习一本通暑假八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年复习大本营期末假期复习一本通暑假八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 如图所示,$∠1和∠2$是对顶角的图形个数是(

A.1个
B.2个
C.3个
D.4个
A
)
A.1个
B.2个
C.3个
D.4个
答案:
【解析】:对顶角的定义为:有公共顶点,并且角的两边互为反向延长线的两个角。
图
(1):∠1和∠2没有公共顶点,不符合对顶角定义。
图
(2):∠1和∠2有公共顶点,但两边不是互为反向延长线,不符合定义。
图
(3):∠1和∠2有公共顶点,且两边互为反向延长线,是对顶角。
图
(4):∠1和∠2有公共顶点,但两边不是互为反向延长线,不符合定义。
综上,只有图
(3)中的∠1和∠2是对顶角,共1个。
【答案】:A
图
(1):∠1和∠2没有公共顶点,不符合对顶角定义。
图
(2):∠1和∠2有公共顶点,但两边不是互为反向延长线,不符合定义。
图
(3):∠1和∠2有公共顶点,且两边互为反向延长线,是对顶角。
图
(4):∠1和∠2有公共顶点,但两边不是互为反向延长线,不符合定义。
综上,只有图
(3)中的∠1和∠2是对顶角,共1个。
【答案】:A
2. 下列说法中正确的是(
A.在同一个平面内,过直线$l上的一点作l$的垂线不止一条
B.直线$l$的垂线有无数条
C.如果两条线段不相交,那么这两条线段就不可能互相垂直
D.过直线$l上的一点A和直线l外的一点B可画一条直线与l$垂直
B
)A.在同一个平面内,过直线$l上的一点作l$的垂线不止一条
B.直线$l$的垂线有无数条
C.如果两条线段不相交,那么这两条线段就不可能互相垂直
D.过直线$l上的一点A和直线l外的一点B可画一条直线与l$垂直
答案:
【解析】:
A选项:在同一平面内,过直线$l$上的一点,只能作出一条与$l$垂直的直线,因此A选项错误。
B选项:对于任意一条直线$l$,我们可以在直线$l$的任意位置、任意方向上作垂线,因此直线$l$的垂线有无数条,B选项正确。
C选项:两条线段不相交,并不意味着它们不能垂直。例如,两条线段分别在两条互相垂直的直线上,且没有交点,但这两条线段仍然是垂直的。因此C选项错误。
D选项:过直线$l$上的一点$A$和直线$l$外的一点$B$,如果$AB$与$l$不垂直,则过点$A$无法作出与$l$垂直且经过点$B$的直线。因此D选项错误。
【答案】:B
A选项:在同一平面内,过直线$l$上的一点,只能作出一条与$l$垂直的直线,因此A选项错误。
B选项:对于任意一条直线$l$,我们可以在直线$l$的任意位置、任意方向上作垂线,因此直线$l$的垂线有无数条,B选项正确。
C选项:两条线段不相交,并不意味着它们不能垂直。例如,两条线段分别在两条互相垂直的直线上,且没有交点,但这两条线段仍然是垂直的。因此C选项错误。
D选项:过直线$l$上的一点$A$和直线$l$外的一点$B$,如果$AB$与$l$不垂直,则过点$A$无法作出与$l$垂直且经过点$B$的直线。因此D选项错误。
【答案】:B
3. 如图所示,下列说法不正确的是(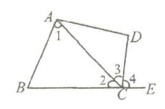
A.$∠1与∠2$是同旁内角
B.$∠1与∠ACE$是内错角
C.$∠B与∠4$是同位角
D.不能得到$∠1和∠3$是内错角
D
)
A.$∠1与∠2$是同旁内角
B.$∠1与∠ACE$是内错角
C.$∠B与∠4$是同位角
D.不能得到$∠1和∠3$是内错角
答案:
【解析】:
对于选项A:观察图可知$∠1$与$∠2$是直线$AB$,$DE$被直线$BC$所截形成的同旁内角,所以A选项正确。
对于选项B:观察图可知$∠1$与$∠ACE$是直线$AB$,$DE$被直线$AC$所截形成的内错角,所以B选项正确。
对于选项C:观察图可知$∠B$与$∠4$是直线$AB$,$CD$被直线$BE$所截形成的同位角,所以C选项正确。
对于选项D:观察图可知,当直线$BE$,$AC$被直线$DE$所截时,$∠1$和$∠3$是内错角,所以D选项错误。
【答案】:D
对于选项A:观察图可知$∠1$与$∠2$是直线$AB$,$DE$被直线$BC$所截形成的同旁内角,所以A选项正确。
对于选项B:观察图可知$∠1$与$∠ACE$是直线$AB$,$DE$被直线$AC$所截形成的内错角,所以B选项正确。
对于选项C:观察图可知$∠B$与$∠4$是直线$AB$,$CD$被直线$BE$所截形成的同位角,所以C选项正确。
对于选项D:观察图可知,当直线$BE$,$AC$被直线$DE$所截时,$∠1$和$∠3$是内错角,所以D选项错误。
【答案】:D
4. 已知$∠α=32^{\circ }$,则$∠α$的补角为( )
A.$58^{\circ }$
B.$68^{\circ }$
C.$148^{\circ }$
D.$168^{\circ }$
A.$58^{\circ }$
B.$68^{\circ }$
C.$148^{\circ }$
D.$168^{\circ }$
答案:
【解析】:
已知角$∠α=32^{\circ}$,根据补角的定义,两个角的和为$180^{\circ}$。
因此,$∠α$的补角为:
$180^{\circ}-32^{\circ}=148^{\circ}$
【答案】:C.$148^{\circ}$
已知角$∠α=32^{\circ}$,根据补角的定义,两个角的和为$180^{\circ}$。
因此,$∠α$的补角为:
$180^{\circ}-32^{\circ}=148^{\circ}$
【答案】:C.$148^{\circ}$
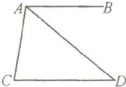
5. 如图所示,$AB// CD$,$∠C= 80^{\circ }$,$∠CAD= 60^{\circ }$,则$∠BAD$的度数等于(
A.$60^{\circ }$
B.$50^{\circ }$
C.$45^{\circ }$
D.$40^{\circ }$
D
)
A.$60^{\circ }$
B.$50^{\circ }$
C.$45^{\circ }$
D.$40^{\circ }$
答案:
【解析】:因为 $AB // CD$,根据两直线平行,同旁内角互补,所以$\angle BAC + \angle C=180^{\circ}$。已知$\angle C = 80^{\circ}$,则$\angle BAC=180^{\circ}-\angle C = 180^{\circ}-80^{\circ}=100^{\circ}$。又因为$\angle CAD = 60^{\circ}$,所以$\angle BAD=\angle BAC-\angle CAD=100^{\circ}-60^{\circ}=40^{\circ}$。
【答案】:D
【答案】:D
6. 下列说法正确的是(
A.过一点有且只有一条直线与已知直线平行
B.平面内,过一点有且只有一条直线与已知直线垂直
C.因为$a// b$,$c// d$,所以$a// d$
D.一条直线的平行线只有一条
B
)A.过一点有且只有一条直线与已知直线平行
B.平面内,过一点有且只有一条直线与已知直线垂直
C.因为$a// b$,$c// d$,所以$a// d$
D.一条直线的平行线只有一条
答案:
【解析】:
A选项:根据平行公理,经过直线外一点,有且只有一条直线与这条直线平行。但A选项的描述中缺少了“直线外”这一关键信息,因此A选项是错误的。
B选项:在平面内,根据垂直的定义和性质,我们知道过一点有且仅有一条直线与已知直线垂直。因此B选项是正确的。
C选项:平行线的传递性是在同一平面内,如果两条直线都与第三条直线平行,那么这两条直线也平行。但C选项中给出了$a// b$和$c// d$,并没有说明$b$和$c$或$d$的关系,或者$a$和$d$在同一平面内,因此不能直接推断出$a// d$。所以C选项是错误的。
D选项:一条直线的平行线有无数条,因为只要保持与这条直线的距离不变并平行移动,就可以得到无数条这样的平行线。所以D选项是错误的。
综上所述,只有B选项是正确的。
【答案】:B
A选项:根据平行公理,经过直线外一点,有且只有一条直线与这条直线平行。但A选项的描述中缺少了“直线外”这一关键信息,因此A选项是错误的。
B选项:在平面内,根据垂直的定义和性质,我们知道过一点有且仅有一条直线与已知直线垂直。因此B选项是正确的。
C选项:平行线的传递性是在同一平面内,如果两条直线都与第三条直线平行,那么这两条直线也平行。但C选项中给出了$a// b$和$c// d$,并没有说明$b$和$c$或$d$的关系,或者$a$和$d$在同一平面内,因此不能直接推断出$a// d$。所以C选项是错误的。
D选项:一条直线的平行线有无数条,因为只要保持与这条直线的距离不变并平行移动,就可以得到无数条这样的平行线。所以D选项是错误的。
综上所述,只有B选项是正确的。
【答案】:B
7. 如图所示,下列条件中,能判断直线$l_{1}// l_{2}$的是(

A.$∠2= ∠3$
B.$∠1= ∠3$
C.$∠4+∠5= 180^{\circ }$
D.$∠2= ∠4$
B
)
A.$∠2= ∠3$
B.$∠1= ∠3$
C.$∠4+∠5= 180^{\circ }$
D.$∠2= ∠4$
答案:
【解析】:
A. 选项A中,$\angle 2$ 和 $\angle 3$ 为同旁内角。只有当$\angle 2+\angle 3=180^\circ$时,才能判定$l_1 // l_2$,故A错误;
B. 选项B中,$\angle 1$ 和 $\angle 3$ 为同位角。根据同位角相等,两直线平行的判定定理,若$\angle 1 = \angle 3$,则$l_1 // l_2$,故B正确;
C. 选项C中,$\angle 4$ 和 $\angle 5$ 为邻补角,$\angle 4+\angle 5= 180^\circ$,无法判定$l_1 // l_2$,故C错误;
D. 选项D中,$\angle 2$ 和 $\angle 4$ 是对顶角,$\angle 2=\angle 4$无法判定$l_1 // l_2$,故D错误。
【答案】:B
A. 选项A中,$\angle 2$ 和 $\angle 3$ 为同旁内角。只有当$\angle 2+\angle 3=180^\circ$时,才能判定$l_1 // l_2$,故A错误;
B. 选项B中,$\angle 1$ 和 $\angle 3$ 为同位角。根据同位角相等,两直线平行的判定定理,若$\angle 1 = \angle 3$,则$l_1 // l_2$,故B正确;
C. 选项C中,$\angle 4$ 和 $\angle 5$ 为邻补角,$\angle 4+\angle 5= 180^\circ$,无法判定$l_1 // l_2$,故C错误;
D. 选项D中,$\angle 2$ 和 $\angle 4$ 是对顶角,$\angle 2=\angle 4$无法判定$l_1 // l_2$,故D错误。
【答案】:B
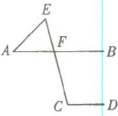
8. 如右图所示,已知直线$AB// CD$,$∠C= 125^{\circ }$,$∠A= 45^{\circ }$,那么$∠E$的大小为(
A.$70^{\circ }$
B.$80^{\circ }$
C.$90^{\circ }$
D.$100^{\circ }$
B
)
A.$70^{\circ }$
B.$80^{\circ }$
C.$90^{\circ }$
D.$100^{\circ }$
答案:
【解析】:因为直线$AB// CD$,$\angle C = 125^{\circ}$,所以$\angle EFB$与$\angle C$是同位角,$\angle EFB=\angle C = 125^{\circ}$。又因为$\angle EFB$是$\triangle AEF$的外角,$\angle A = 45^{\circ}$,根据三角形外角等于不相邻两个内角之和,可得$\angle E=\angle EFB-\angle A=125^{\circ}-45^{\circ}=80^{\circ}$。
【答案】:B
【答案】:B
9. 下列说法:①一个锐角的余角是锐角;②一个角的补角一定是钝角;③相等的角一定是对顶角;④若$∠α与∠β$互补,$∠α与∠γ$互补,则$∠β与∠γ$互补。其中正确的说法有(
A.1个
B.2个
C.3个
D.4个
A
)A.1个
B.2个
C.3个
D.4个
答案:
【解析】:
①一个锐角的余角是锐角:锐角是小于$90^\circ$的角,其余角为$90^\circ$减去这个锐角,结果仍然小于$90^\circ$,所以是锐角。这个说法是正确的。
②一个角的补角一定是钝角:补角是两个角的和为$180^\circ$。例如,$90^\circ$的补角是$90^\circ$,是直角而非钝角。所以这个说法是错误的。
③相等的角一定是对顶角:对顶角一定相等,但相等的角不一定是对顶角。例如,两个直角三角形的直角都是$90^\circ$,但它们不是对顶角。所以这个说法是错误的。
④若$\angle \alpha$与$\angle \beta$互补,$\angle \alpha$与$\angle \gamma$互补,则$\angle \beta$与$\angle \gamma$互补:如果$\angle \alpha$与$\angle \beta$互补,那么$\angle \alpha + \angle \beta = 180^\circ$;同理,$\angle \alpha + \angle \gamma = 180^\circ$。由此可得$\angle \beta = \angle \gamma$,但这并不意味着$\angle \beta$与$\angle \gamma$互补,它们只是相等。所以这个说法是错误的。
综上所述,只有①是正确的。
【答案】:A
①一个锐角的余角是锐角:锐角是小于$90^\circ$的角,其余角为$90^\circ$减去这个锐角,结果仍然小于$90^\circ$,所以是锐角。这个说法是正确的。
②一个角的补角一定是钝角:补角是两个角的和为$180^\circ$。例如,$90^\circ$的补角是$90^\circ$,是直角而非钝角。所以这个说法是错误的。
③相等的角一定是对顶角:对顶角一定相等,但相等的角不一定是对顶角。例如,两个直角三角形的直角都是$90^\circ$,但它们不是对顶角。所以这个说法是错误的。
④若$\angle \alpha$与$\angle \beta$互补,$\angle \alpha$与$\angle \gamma$互补,则$\angle \beta$与$\angle \gamma$互补:如果$\angle \alpha$与$\angle \beta$互补,那么$\angle \alpha + \angle \beta = 180^\circ$;同理,$\angle \alpha + \angle \gamma = 180^\circ$。由此可得$\angle \beta = \angle \gamma$,但这并不意味着$\angle \beta$与$\angle \gamma$互补,它们只是相等。所以这个说法是错误的。
综上所述,只有①是正确的。
【答案】:A
10. 如右图所示,点$O在直线AB$上,且$∠COA= 36^{\circ }$,则$∠DOB$的大小为(

A.$38^{\circ }$
B.$54^{\circ }$
C.$64^{\circ }$
D.$72^{\circ }$
B
)
A.$38^{\circ }$
B.$54^{\circ }$
C.$64^{\circ }$
D.$72^{\circ }$
答案:
【解析】:因为点$O$在直线$AB$上,所以$\angle AOB = 180^{\circ}$。观察图形可知,$\angle COD = 90^{\circ}$(图中有直角符号)。已知$\angle COA = 36^{\circ}$,则$\angle AOC + \angle COD + \angle DOB = 180^{\circ}$,即$36^{\circ} + 90^{\circ} + \angle DOB = 180^{\circ}$,解得$\angle DOB = 180^{\circ} - 36^{\circ} - 90^{\circ} = 54^{\circ}$。
【答案】:B
【答案】:B
11. 如右图所示,点$C在∠AOB的OB$边上,用尺规作出了$CN// OA$,作图痕迹中,弧$FG$是(

A.以点$C$为圆心,$OD$为半径的弧
B.以点$C$为圆心,$DM$为半径的弧
C.以点$E$为圆心,$OD$为半径的弧
D.以点$E$为圆心,$DM$为半径的弧
D
)
A.以点$C$为圆心,$OD$为半径的弧
B.以点$C$为圆心,$DM$为半径的弧
C.以点$E$为圆心,$OD$为半径的弧
D.以点$E$为圆心,$DM$为半径的弧
答案:
【解析】:要作$CN// OA$,根据尺规作一个角等于已知角的方法,需以点$O$为圆心,任意长为半径画弧,交$OA$于点$M$,交$OB$于点$D$;再以点$C$为圆心,$OM$(或$OD$)为半径画弧,交$OB$于点$E$;然后以点$E$为圆心,$DM$为半径画弧,交前弧于点$F$,过点$C$、$F$作射线$CN$,则$CN// OA$。观察作图痕迹,弧$FG$是以点$E$为圆心,$DM$为半径的弧。
【答案】:D
【答案】:D
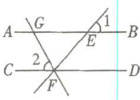
12. 如图,直线$AB// CD$,直线$EF分别交直线AB$,$CD于点E$,$F$,过点$F作FG⊥FE$,交直线$AB于点G$。若$∠1= 42^{\circ }$,则$∠2$的大小是(
A.$56^{\circ }$
B.$48^{\circ }$
C.$46^{\circ }$
D.$40^{\circ }$
$48^{\circ}$
)
A.$56^{\circ }$
B.$48^{\circ }$
C.$46^{\circ }$
D.$40^{\circ }$
答案:
【解析】:
因为$AB// CD$,$\angle 1 = 42^{\circ}$,根据两直线平行,同位角相等,可得$\angle EFD=\angle 1 = 42^{\circ}$。
因为$FG\perp FE$,所以$\angle GFE = 90^{\circ}$。
又因为$\angle 2+\angle EFD+\angle GFE = 180^{\circ}$(平角的定义),所以$\angle 2=180^{\circ}-\angle GFE-\angle EFD = 180^{\circ}-90^{\circ}-42^{\circ}=48^{\circ}$。
【答案】:$48^{\circ}$
因为$AB// CD$,$\angle 1 = 42^{\circ}$,根据两直线平行,同位角相等,可得$\angle EFD=\angle 1 = 42^{\circ}$。
因为$FG\perp FE$,所以$\angle GFE = 90^{\circ}$。
又因为$\angle 2+\angle EFD+\angle GFE = 180^{\circ}$(平角的定义),所以$\angle 2=180^{\circ}-\angle GFE-\angle EFD = 180^{\circ}-90^{\circ}-42^{\circ}=48^{\circ}$。
【答案】:$48^{\circ}$
查看更多完整答案,请扫码查看


