《2025年复习大本营期末假期复习一本通暑假八年级数学北师大版》

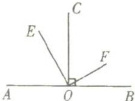
例1 如图,$OC\perp AB$,$\angle AOE= \angle COF$,则射线$OE$,$OF$是什么位置关系？请说明理由。

答案： 【解析】：
此题中要确定射线$OE$和$OF$的位置关系，需利用已知条件$OC\perp AB$，所以$\angle AOC = 90^{\circ}$。
又因为$\angle AOE=\angle COF$，通过等量代换可得$\angle AOE+\angle COE=\angle COF+\angle COE$，即$\angle EOF=\angle AOC = 90^{\circ}$，从而得出$OE$与$OF$互相垂直。
【答案】：
射线$OE$与$OF$互相垂直。

【针对训练1】如图所示,$OA\perp OC$,$OB\perp OD$,$\angle AOB= 150^{\circ}$,求$\angle COD$的度数。

答案： 【解析】：因为 $OA \perp OC$，所以 $\angle AOC = 90^{\circ}$；又因为 $OB \perp OD$，所以 $\angle BOD = 90^{\circ}$。已知 $\angle AOB = 150^{\circ}$，而 $\angle AOB = \angle AOD + \angle DOB$，所以 $\angle AOD = \angle AOB - \angle DOB = 150^{\circ} - 90^{\circ} = 60^{\circ}$。又因为 $\angle AOC = \angle AOD + \angle COD = 90^{\circ}$，所以 $\angle COD = \angle AOC - \angle AOD = 90^{\circ} - 60^{\circ} = 30^{\circ}$。
【答案】：30°

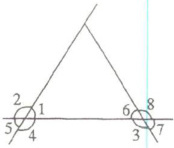
例2 如图所示,$\angle 1+\angle 3= 180^{\circ}$,则图中与$\angle 1$相等的角的个数有3个,与$\angle 1$互补的角的个数有4个。

答案： 【解析】：
由对顶角相等，得$\angle 1 = \angle 5$。
由已知条件$\angle 1 + \angle 3 = 180^\circ$，可知$\angle 3$是$\angle 1$的补角。
因为$\angle 6$和$\angle 7$都是$\angle 3$的邻补角，所以$\angle 6 = \angle 7 = \angle 1$。
因此，图中与$\angle 1$相等的角有$\angle 5$、$\angle 6$、$\angle 7$，共3个。
$\angle 1$的补角有$\angle 2$、$\angle 4$、$\angle 3$、$\angle 8$，共4个。
【答案】：3；4