《2025年复习大本营期末假期复习一本通暑假八年级数学北师大版》

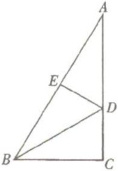
21. 如下图所示,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$D$、$E$ 分别为 $AC$、$AB$ 上的点,且 $AD = BD$,$AE = BC$,$DE = DC$. 求证：$DE \perp AB$.

答案： 【解析】：
1. 因为$AD=BD$，$AE=BC$，$DE=DC$，
根据边边边全等定理，$\triangle ADE\cong \triangle BCD$。
2. 由于$\triangle ADE\cong \triangle BCD$，
所以$\angle AED=\angle C$。
3. 已知$\angle C=90^\circ$，
所以$\angle AED=90^\circ$。
4. 因此$DE\perp AB$。
【答案】：
$DE\perp AB$

22. 如下图所示,要测量河岸相对两点 $A$,$B$ 的距离,可以从 $AB$ 的垂线 $BF$ 上取两点 $C$、$D$,使 $BC = CD$,过 $D$ 作 $DE \perp BF$,且 $A$,$C$,$E$ 三点在同一直线上. 若测得 $DE = 15m$,即可知道 $AB$ 也为 $15m$,请你说明理由.

答案： 【解析】：
因为$DE\perp BF$，$AB\perp BF$，
所以$\angle ABC=\angle EDC=90^\circ$。
又因为$BC=CD$，$\angle ACB$和$\angle ECD$为对顶角，
根据三角形全等（ASA）判定定理：
两个三角形对应的两角及其夹边相等时，这两个三角形全等。‌
在$\triangle ABC$和$\triangle EDC$中：
$\left\{\begin{matrix}\angle ABC=\angle EDC,\\BC=CD,\\\angle ACB=\angle ECD.\end{matrix}\right.$
所以$\triangle ABC\cong\triangle EDC$。
根据全等三角形的性质对应边都相等，
所以$AB=DE=15$米。
【答案】：过$D$作$DE \perp BF$，且$A$，$C$，$E$三点在同一直线上，使$\angle ABC=\angle EDC=90^\circ$，$BC=CD$，$\angle ACB=\angle ECD$，则$\triangle ABC\cong\triangle EDC$，所以$AB=DE=15$米。

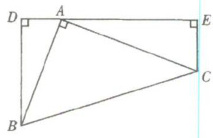
23. 如下图所示,$AB = AC$,$DE$ 是过点 $A$ 的一条直线,且 $B$、$C$ 两点在 $DE$ 的同侧,$BD \perp DE$ 于点 $D$,$CE \perp DE$ 于点 $E$,试说明：$BD = DE - CE$.

答案： 【解析】：因为 $ BD \perp DE $，$ CE \perp DE $，所以 $ \angle ADB = \angle AEC = 90^\circ $。
由于 $ AB = AC $，且 $ \angle BAD + \angle CAE = 90^\circ $（因为 $ \angle BAC = 90^\circ $），同时 $ \angle ACE + \angle CAE = 90^\circ $，故 $ \angle BAD = \angle ACE $。
在 $ \triangle ABD $ 和 $ \triangle CAE $ 中，
$ \angle ADB = \angle CEA = 90^\circ $，
$ \angle BAD = \angle ACE $，
$ AB = CA $，
所以 $ \triangle ABD \cong \triangle CAE $（AAS）。
因此，$ BD = AE $，$ AD = CE $。
又因为 $ DE = AD + AE $，所以 $ DE = CE + BD $，即 $ BD = DE - CE $。
【答案】：$ BD = DE - CE $

24. 如下图所示,在梯形 $ABCD$ 中,已知 $AD // BC$,$AB = CD$,延长线段 $CB$ 到 $E$,使 $BE = AD$,连接 $AE$、$AC$.
(1) 求证：$\triangle ABE \cong \triangle CDA$；
(2) 若$\angle DAC = 40^{\circ}$,求$\angle EAC$的度数.

答案： 【解析】：
(1) 因为在梯形 $ABCD$ 中，$AD // BC$，$AB = CD$，所以梯形 $ABCD$ 是等腰梯形，因此$\angle ABC=\angle DCB$。又因为$AD // BC$，所以$\angle DAC = \angle ACB$（两直线平行，内错角相等）。由于$\angle ABE + \angle ABC = 180^{\circ}$，$\angle ADC + \angle DCB = 180^{\circ}$，且$\angle ABC = \angle DCB$，所以$\angle ABE=\angle ADC$。已知$BE = AD$，$AB = CD$，根据全等三角形判定定理（SAS），可得$\triangle ABE \cong \triangle CDA$。
(2) 由
(1)知$\triangle ABE \cong \triangle CDA$，所以$\angle BAE=\angle DCA$。因为$AD // BC$，所以$\angle DAC=\angle ACB = 40^{\circ}$。在等腰梯形$ABCD$中，$AB = CD$，所以$\angle DCA=\angle BAC$（等腰梯形同一底上的两个角相等，且对角线相等，可推出底角平分线相关性质，此处也可通过三角形全等对应角相等及平行线性质推导），即$\angle BAE=\angle BAC$。设$\angle BAC = x$，则$\angle BAE=x$，$\angle EAC=\angle BAE+\angle BAC = 2x$。在$\triangle ABC$中，$\angle ABC+\angle BAC+\angle ACB=180^{\circ}$，而$\angle ABC = \angle DCB$，$\angle DCB=\angle DCA+\angle ACB=x + 40^{\circ}$，所以$(x + 40^{\circ})+x+40^{\circ}=180^{\circ}$，解得$x = 50^{\circ}$，因此$\angle EAC=2x = 100^{\circ}$。
【答案】：
(1) 证明见解析；
(2) $100^{\circ}$