2025年复习大本营期末假期复习一本通暑假八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年复习大本营期末假期复习一本通暑假八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
14. 如下图,在$Rt△ABC$中,$∠C= 90^{\circ }$,BD平分$∠ABC$,$DE⊥AB$于E,则:
(1)与DE相等的线段是______
(2)若$AB= 10$,$BC= 8$,$AC= 6$,则$BE= $______

(1)与DE相等的线段是______
DC
,理由是______角平分线上的点到角两边的距离相等
;(2)若$AB= 10$,$BC= 8$,$AC= 6$,则$BE= $______
8
,$AE= $______2
,$△AED$的周长= ______8
。
答案:
【解析】:(1)因为BD平分∠ABC,∠C=90°(即DC⊥BC),DE⊥AB,根据角平分线的性质:角平分线上的点到角两边的距离相等,所以DE=DC。
(2)在Rt△BDE和Rt△BDC中,BD=BD,DE=DC(已证),所以Rt△BDE≌Rt△BDC(HL),则BE=BC=8。因为AB=10,所以AE=AB - BE=10 - 8=2。△AED的周长=AE + DE + AD,又因为DE=DC,所以周长=AE + DC + AD=AE + AC=2 + 6=8。
【答案】:
(1)DC,角平分线上的点到角两边的距离相等;
(2)8,2,8
(2)在Rt△BDE和Rt△BDC中,BD=BD,DE=DC(已证),所以Rt△BDE≌Rt△BDC(HL),则BE=BC=8。因为AB=10,所以AE=AB - BE=10 - 8=2。△AED的周长=AE + DE + AD,又因为DE=DC,所以周长=AE + DC + AD=AE + AC=2 + 6=8。
【答案】:
(1)DC,角平分线上的点到角两边的距离相等;
(2)8,2,8
15. 如上图,在$△ABC$中,$AB= AC= 3cm$,AB的垂直平分线交AC于点N,$△BCN$的周长是5cm,则BC的长等于

2
cm。
答案:
【解析】:因为MN是AB的垂直平分线,根据垂直平分线的性质,垂直平分线上的点到线段两端的距离相等,所以AN=BN。
已知△BCN的周长是5cm,即BC+CN+BN=5cm。又因为AN=BN,且AC=AN+CN=3cm,所以BN+CN=AN+CN=AC=3cm。
将BN+CN=3cm代入△BCN的周长公式,可得BC+3cm=5cm,解得BC=5cm-3cm=2cm。
【答案】:2
已知△BCN的周长是5cm,即BC+CN+BN=5cm。又因为AN=BN,且AC=AN+CN=3cm,所以BN+CN=AN+CN=AC=3cm。
将BN+CN=3cm代入△BCN的周长公式,可得BC+3cm=5cm,解得BC=5cm-3cm=2cm。
【答案】:2
16. 如右图,CD与BE互相垂直平分,$AD⊥DB$,$∠DBE= 70^{\circ }$,则$∠DEB= $
70
°。
答案:
【解析】:因为CD与BE互相垂直平分,设交点为F,则BF=EF,CF=DF,且BE⊥CD。所以△BFD≌△BFC≌△EFD≌△EFC(SAS),可得BD=BC=ED=EC,即四边形BCED是菱形。
在菱形BCED中,BE是对角线,所以BE平分∠DBC和∠DEC。已知∠DBE=70°,则∠DBC=2∠DBE=140°。
因为AD⊥DB,所以∠ADB=90°,但此条件在求∠DEB时暂未直接用到。在△BED中,BF=EF,BE⊥CD,所以△BED是等腰三角形(BD=ED),BF是底边ED上的高、中线和角平分线(三线合一)。
在Rt△BFD中,∠DBF=70°,则∠BDF=90°-70°=20°。因为菱形的对角线平分一组对角,所以∠EDF=∠BDF=20°。
在Rt△EFD中,∠EFD=90°,∠EDF=20°,所以∠DEF=90°-20°=70°,即∠DEB=70°。
【答案】:70
在菱形BCED中,BE是对角线,所以BE平分∠DBC和∠DEC。已知∠DBE=70°,则∠DBC=2∠DBE=140°。
因为AD⊥DB,所以∠ADB=90°,但此条件在求∠DEB时暂未直接用到。在△BED中,BF=EF,BE⊥CD,所以△BED是等腰三角形(BD=ED),BF是底边ED上的高、中线和角平分线(三线合一)。
在Rt△BFD中,∠DBF=70°,则∠BDF=90°-70°=20°。因为菱形的对角线平分一组对角,所以∠EDF=∠BDF=20°。
在Rt△EFD中,∠EFD=90°,∠EDF=20°,所以∠DEF=90°-20°=70°,即∠DEB=70°。
【答案】:70
17. 如下图所示的轴对称图形。(1)找出它的对称轴;(2)线段DF与对称轴有什么关系?连接D,H两点的线段呢?(3)线段AB与AH有什么关系?线段BC与GH,CD与GF呢?(4)$∠D与∠F$有什么关系?


答案:
【解析】:
(1)在轴对称图形中,对称轴是使图形沿某条直线折叠后,直线两旁的部分能够完全重合的直线。观察图形,从点A到点E的这条竖直直线能使图形左右两边完全重合,所以对称轴是直线AE。
(2)对于线段DF,沿对称轴AE折叠,点D会与点F重合,所以DF被对称轴AE垂直平分;连接D、H两点,观察图形可知线段DH与对称轴AE不垂直也不平分,它们是相交关系。
(3)根据轴对称图形的性质,对应线段相等。AB和AH是关于对称轴对称的对应线段,所以AB=AH;同理,BC和GH是对应线段,BC=GH;CD和GF是对应线段,CD=GF。
(4)∠D与∠F是关于对称轴对称的对应角,根据轴对称性质,对应角相等,所以∠D=∠F。
【答案】:
(1)直线AE;
(2)DF被对称轴垂直平分,线段DH与对称轴相交;
(3)AB=AH,BC=GH,CD=GF;
(4)∠D=∠F
(1)在轴对称图形中,对称轴是使图形沿某条直线折叠后,直线两旁的部分能够完全重合的直线。观察图形,从点A到点E的这条竖直直线能使图形左右两边完全重合,所以对称轴是直线AE。
(2)对于线段DF,沿对称轴AE折叠,点D会与点F重合,所以DF被对称轴AE垂直平分;连接D、H两点,观察图形可知线段DH与对称轴AE不垂直也不平分,它们是相交关系。
(3)根据轴对称图形的性质,对应线段相等。AB和AH是关于对称轴对称的对应线段,所以AB=AH;同理,BC和GH是对应线段,BC=GH;CD和GF是对应线段,CD=GF。
(4)∠D与∠F是关于对称轴对称的对应角,根据轴对称性质,对应角相等,所以∠D=∠F。
【答案】:
(1)直线AE;
(2)DF被对称轴垂直平分,线段DH与对称轴相交;
(3)AB=AH,BC=GH,CD=GF;
(4)∠D=∠F
18. 如下图所示,作出$△ABC$关于直线BC对称的图形。


答案:
【解析】:
找到三角形$ABC$各顶点关于直线$BC$的对称点。具体步骤如下:
确定点$A$关于直线$BC$的对称点$A'$。可以通过作点$A$到直线$BC$的垂线,并延长至等距离处得到$A'$。
点$B$和点$C$都在直线$BC$上,因此它们关于直线$BC$的对称点就是它们自身,即$B' = B$,$C' = C$。
连接对称点$A'$,$B$,$C$,得到对称三角形$A'BC$。
【答案】:作出位置与点$A$关于直线$BC$对称的点$A'$,连接$A'B$,$A'C$,得到$△A'BC$即为$△ABC$关于直线BC对称的图形。
找到三角形$ABC$各顶点关于直线$BC$的对称点。具体步骤如下:
确定点$A$关于直线$BC$的对称点$A'$。可以通过作点$A$到直线$BC$的垂线,并延长至等距离处得到$A'$。
点$B$和点$C$都在直线$BC$上,因此它们关于直线$BC$的对称点就是它们自身,即$B' = B$,$C' = C$。
连接对称点$A'$,$B$,$C$,得到对称三角形$A'BC$。
【答案】:作出位置与点$A$关于直线$BC$对称的点$A'$,连接$A'B$,$A'C$,得到$△A'BC$即为$△ABC$关于直线BC对称的图形。
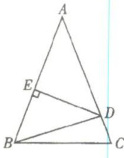
19. 如图所示,有一块三角形田地,$AB= AC= 10m$,作AB的垂直平分线ED交AC于点D,交AB于点E,量得$△BDC$的周长为17m,请你替测量人员计算BC的长。

答案:
【解析】:
由于$ED$是$AB$的垂直平分线,根据垂直平分线的性质,我们知道垂直平分线上的点到线段两端的距离相等,即$DA=DB$。
已知$\triangle BDC$的周长为$17m$,根据三角形的周长定义,有$BD+DC+BC=17$。
由于$DA=DB$,我们可以将$BD$替换为$DA$,得到$DA+DC+BC=17$。
又因为$DA+DC=AC$,所以$AC+BC=17$。
已知$AC=10m$,代入上式,得到$10+BC=17$。
解这个方程,我们得到$BC=7m$。
【答案】:
$BC=7m$
由于$ED$是$AB$的垂直平分线,根据垂直平分线的性质,我们知道垂直平分线上的点到线段两端的距离相等,即$DA=DB$。
已知$\triangle BDC$的周长为$17m$,根据三角形的周长定义,有$BD+DC+BC=17$。
由于$DA=DB$,我们可以将$BD$替换为$DA$,得到$DA+DC+BC=17$。
又因为$DA+DC=AC$,所以$AC+BC=17$。
已知$AC=10m$,代入上式,得到$10+BC=17$。
解这个方程,我们得到$BC=7m$。
【答案】:
$BC=7m$
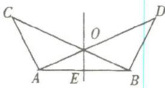
20. 如图所示,$∠BAC= ∠ABD$,$AC= BD$,点O是AD、BC的交点,点E是AB的中点。试判断OE和AB的位置关系,并给出证明。

答案:
【解析】:
首先,我们可以通过以下步骤证明OE垂直于AB:
1. 在三角形OAB中,由于点E是AB的中点,如果要证明OE垂直于AB,只需要证明OE是等腰三角形OAB底边AB上的中线即可。
2. 已知$AC=BD$,$∠BAC=∠ABD$,$AB=AB$(公共边),所以根据SAS(边-角-边)全等条件,可以得到$\triangle BAC \cong \triangle ABD$。
3. 由全等三角形的性质可知,$∠C=∠D$。
4. 又因为$AC=BD$,$∠AOC=∠BOD$(对顶角相等),所以根据AAS(角-角-边)全等条件,可以得到$\triangle AOC \cong \triangle BOD$。
5. 由全等三角形的性质可知,$AO=BO$。
6. 因此,在等腰三角形OAB中,由于点E是AB的中点,根据等腰三角形三线合一的性质,OE垂直于AB。
【答案】:
OE垂直于AB。
首先,我们可以通过以下步骤证明OE垂直于AB:
1. 在三角形OAB中,由于点E是AB的中点,如果要证明OE垂直于AB,只需要证明OE是等腰三角形OAB底边AB上的中线即可。
2. 已知$AC=BD$,$∠BAC=∠ABD$,$AB=AB$(公共边),所以根据SAS(边-角-边)全等条件,可以得到$\triangle BAC \cong \triangle ABD$。
3. 由全等三角形的性质可知,$∠C=∠D$。
4. 又因为$AC=BD$,$∠AOC=∠BOD$(对顶角相等),所以根据AAS(角-角-边)全等条件,可以得到$\triangle AOC \cong \triangle BOD$。
5. 由全等三角形的性质可知,$AO=BO$。
6. 因此,在等腰三角形OAB中,由于点E是AB的中点,根据等腰三角形三线合一的性质,OE垂直于AB。
【答案】:
OE垂直于AB。
查看更多完整答案,请扫码查看


