《2025年复习大本营期末假期复习一本通暑假八年级数学北师大版》

3. 如右图所示,一游人要从一个长方形广场的$A到C$,至少要走500米.

答案： 【解析】：
根据题意，游客要从长方形广场的一个顶点 $ A $ 走到对角顶点 $ C $，可以选择沿着长方形的边走，也可以选择沿对角线走。
沿边走：
从 $ A $ 到 $ D $ 再到 $ C $，总距离为 $ 400 $ 米 + $ 300 $ 米 = $ 700 $ 米。
沿对角线走：
使用勾股定理计算对角线的长度。
设 $ AB = 400 $ 米，$ BC = 300 $ 米，则对角线 $ AC $ 的长度为：
$AC = \sqrt{AB^2 + BC^2} = \sqrt{400^2 + 300^2} = \sqrt{160000 + 90000} = \sqrt{250000} = 500$（米）。
比较两种路径的距离：
沿边走的距离是 $ 700 $ 米，沿对角线走的距离是 $ 500 $ 米。
因此，至少要走的距离是 $ 500 $ 米。
【答案】：500米

4. 在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$AB = 17$,$AC = 15$.则$S_{\triangle ABC}= $60.

答案： 【解析】：在直角三角形$ABC$中，已知$\angle C = 90^{\circ}$，$AB = 17$，$AC = 15$。
根据勾股定理，有$BC = \sqrt{AB^{2} - AC^{2}} = \sqrt{17^{2} - 15^{2}} = \sqrt{289 - 225} = \sqrt{64} = 8$。
直角三角形的面积公式为$S = \frac{1}{2} × \text{底} × \text{高}$，
在这里，底和高就是直角三角形的两条直角边$AC$和$BC$。
所以，$S_{\triangle ABC} = \frac{1}{2} × AC × BC = \frac{1}{2} × 15 × 8 = 60$。
【答案】：60

5. 在$\triangle ABC$中,$\angle A = 90^{\circ}$,则下列各式中不成立的是(B)
A.$BC^{2} = AB^{2} + AC^{2}$
B.$AB^{2} = AC^{2} + BC^{2}$
C.$AB^{2} = BC^{2} - AC^{2}$
D.$AC^{2} = BC^{2} - AB^{2}$

答案： 【解析】：
在直角三角形$\triangle ABC$中，由于$\angle A = 90^{\circ}$，根据勾股定理，我们有$BC^{2} = AB^{2} + AC^{2}$。
接下来，我们将逐一检验每个选项：
A. $BC^{2} = AB^{2} + AC^{2}$：这是勾股定理的直接应用，所以A选项是正确的。
B. $AB^{2} = AC^{2} + BC^{2}$：这个等式与勾股定理相矛盾，因为根据勾股定理，$BC^{2}$是$AB^{2}$和$AC^{2}$的和，而不是$AB^{2}$是$AC^{2}$和$BC^{2}$的和。所以B选项是错误的。
C. $AB^{2} = BC^{2} - AC^{2}$：这个等式可以通过勾股定理的等式$BC^{2} = AB^{2} + AC^{2}$进行变形得到，即$AB^{2} = BC^{2} - AC^{2}$，所以C选项是正确的。
D. $AC^{2} = BC^{2} - AB^{2}$：这个等式同样可以通过勾股定理的等式进行变形得到，即$AC^{2} = BC^{2} - AB^{2}$，所以D选项是正确的。
综上所述，不成立的选项是B。
【答案】：B

6. 一直角三角形的两边长分别为$3和4$,则第三边的平方为(25或7)
A.$25$
B.$7$
C.$25或7$
D.$9$

答案： 【解析】：
设第三边为$c$。
当$4$是直角三角形的直角边时，根据勾股定理，有：
$c^2 = 3^2 + 4^2$
$c^2 = 9 + 16$
$c^2 = 25$
当$4$是直角三角形的斜边时，根据勾股定理，有：
$4^2 = 3^2 + c^2$
$c^2 = 4^2 - 3^2$
$c^2 = 16 - 9$
$c^2 = 7$
所以，第三边的平方可能为$25$或$7$。
【答案】：C.$25$或$7$

7. 如下图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$CD\perp AB于D$,$AC = 3$,$AB = 5$,则$CD$的长为(A)
A.$\frac{12}{5}$
B.$2$
C.$\frac{6}{5}$
D.$2.5$

答案： 【解析】：
因为$\angle ACB=90^\circ$，$AC=3$，$AB=5$，由勾股定理可得：
$BC=\sqrt{AB^2-AC^2}=\sqrt{5^2-3^2}=\sqrt{25-9}=\sqrt{16}=4$。
根据直角三角形的面积公式：
$S_{\triangle ABC}=\frac{1}{2}× AC× BC=\frac{1}{2}× AB× CD$。
代入已知数据：
$\frac{1}{2}× 3× 4=\frac{1}{2}× 5× CD$。
解得：
$CD=\frac{3× 4}{5}=\frac{12}{5}$。
【答案】：A

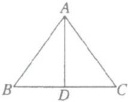
8. 如图,已知一个等腰三角形的周长是$16$,底边上的高是$4$.求这个三角形的各边的长.

答案： 【解析】：
设等腰三角形的腰长为$x$，底边长为$y$，
根据题意，三角形的周长为16，
因此有：$2x+y=16$，
由于三角形是等腰三角形，底边上的高将底边分为两等分，每份长度为$\frac{y}{2}$，
利用勾股定理，在由腰、高和半底边构成的直角三角形中有：
$x^2=4^2+(\frac{y}{2})^2$，
$x^2=16+\frac{y^2}{4}$，
将周长方程$2x+y=16$变形为$y=16-2x$，代入勾股定理方程中，得：
$x^2=16+\frac{(16-2x)^2}{4}$，
展开并化简得：
$4x^2=64+ (16-2x)^2$，
$4x^2=64+256-64x+4x^2$，
化简后得：
$64x=320$，
$x=5$，
将$x=5$代入$y=16-2x$，得：
$y=16-2×5$，
$y=6$，
因此，这个等腰三角形的各边长为：腰长5，底边长6。
【答案】：腰长5，底边长6

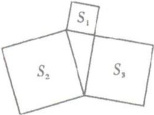
9. 已知,如右图所示,正方形$S_{1}的面积为25$,正方形$S_{2}的面积为169$,那么正方形$S_{3}$的面积为____144.

答案： 【解析】：
设正方形$S_1$、$S_2$、$S_3$的边长分别为$a$、$b$、$c$。
由题意得，$S_1$的面积为$25$，即$a^2 = 25$，所以$a = 5$（边长取正值）；
$S_2$的面积为$169$，即$b^2 = 169$，所以$b = 13$（边长取正值）。
观察图形，可以发现$S_1$、$S_2$、$S_3$三个正方形构成了一个直角三角形，其中$S_1$和$S_3$的边长为直角边，$S_2$的边长为斜边。
根据勾股定理，有$a^2 + c^2 = b^2$。
将已知的$a$和$b$代入，得到$25 + c^2 = 169$。
解这个方程，得到$c^2 = 169 - 25 = 144$。
因为$c$是正方形的边长，所以$c$取正值，即$c = \sqrt{144} = 12$。
但题目要求的是正方形$S_3$的面积，即$c^2 = 144$。
【答案】：144

10. 一轮船以$16$海里/时的速度离开$A$港向东南方向航行,另一艘轮船同时以$12$海里/时的速度向西南方向航行,经过$1.5$小时后,它们相距30海里.

答案： 【解析】：
首先，根据题意，一艘轮船以16海里/时的速度向东南方向航行，另一艘轮船以12海里/时的速度向西南方向航行。东南方向和西南方向是垂直的，因此两艘轮船的航行路线之间的夹角是$90^\circ$。
经过1.5小时，第一艘轮船航行的距离是$16 × 1.5 = 24$海里，第二艘轮船航行的距离是$12 × 1.5 = 18$海里。
由于两艘轮船的航行路线垂直，根据勾股定理，两艘轮船相距的距离$d$可以通过下式计算：
$d = \sqrt{24^2 + 18^2} = \sqrt{576 + 324} = \sqrt{900} = 30 \text{ 海里}$
【答案】：30

11. 如右图,在$Rt\triangle ABC$中,$AB = 9$,$BC = 6$,$\angle B = 90^{\circ}$,将$\triangle ABC$折叠,使$A点与BC的中点D$重合,折痕为$MN$,则线段$BN$的长为____4.

答案： 【解析】：
设 $BN = x$，由于 $D$ 是 $BC$ 的中点，所以 $BD = 3$（因为$BC = 6$）。
由题意，知 $AN = 9 - x$。
由于折叠后 $A$ 点与 $D$ 点重合，所以 $DN = AN = 9 - x$。
在直角三角形 $BND$ 中，根据勾股定理，有：
$DN^2 = BN^2 + BD^2$，
代入已知数值，得：
$(9 - x)^2 = x^2 + 3^2$，
$81 - 18x + x^2 = x^2 + 9$，
$81 - 18x = 9$，
$18x = 72$，
$x = 4$。
所以，线段 $BN$ 的长为 $4$。
【答案】：4

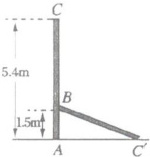
12. 如下图,马路边一根高为$5.4m$的电线杆,被一辆卡车从离地面$1.5m$处撞断裂,倒下的电线杆顶部是否会落在离它的底部$4m$的快车道上？

答案： 【解析】：电线杆断裂处为点B，底部为点A，顶部落点为点C。已知电线杆总高5.4m，断裂处离地面1.5m，所以AB=1.5m，断裂部分BC=5.4 - 1.5=3.9m。倒下后，BC为斜边，AB为直角边，设顶部落点C到底部A的距离为AC，在直角三角形ABC中，根据勾股定理，AC² + AB² = BC²，即AC² + 1.5² = 3.9²。计算可得AC²=3.9² - 1.5²=(3.9 - 1.5)(3.9 + 1.5)=2.4×5.4=12.96，所以AC=3.6m。因为3.6m＜4m，所以倒下的电线杆顶部不会落在离底部4m的快车道上。
【答案】：不会

13. 如下图所示,在四边形$ABCF$中,$\angle ABC = 90^{\circ}$,$\angle CAF = 90^{\circ}$,$AB = 8$,$BC = 6$,$AF = 24$,求正方形$CDEF$的面积.

答案： 【解析】：
因为$\angle ABC=90^{\circ}$，$AB=8$，$BC=6$，
根据勾股定理：
$AC^2=AB^2+BC^2=8^2+6^2=64+36=100$，
所以$AC=\sqrt{100}=10$，
因为$\angle CAF=90^{\circ}$，$AF=24$，
再次使用勾股定理：
$CF^2=AC^2+AF^2=10^2+24^2=100+576=676$，
因为四边形$CDEF$是正方形，
所以正方形$CDEF$的面积为：
$S_{CDEF}=CF^2=676$，
【答案】：676