2025年复习大本营期末假期复习一本通暑假八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年复习大本营期末假期复习一本通暑假八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 若一个三角形的三个内角的度数之比为 $2:3:7$,这个三角形一定是(
A.直角三角形
B.等腰三角形
C.锐角三角形
D.钝角三角形
D
)A.直角三角形
B.等腰三角形
C.锐角三角形
D.钝角三角形
答案:
【解析】:设三角形的三个内角的度数分别为 $2x$,$3x$ 和 $7x$。
根据三角形内角和为 $180^\circ$ 的性质,我们有:
$2x + 3x + 7x = 180^\circ$
$12x = 180^\circ$
$x = 15^\circ$
代入 $x = 15^\circ$,得到三个内角的度数分别为:
$2x = 30^\circ$
$3x = 45^\circ$
$7x = 105^\circ$
由于 $105^\circ$ 是钝角,因此这个三角形是钝角三角形。
【答案】:D
根据三角形内角和为 $180^\circ$ 的性质,我们有:
$2x + 3x + 7x = 180^\circ$
$12x = 180^\circ$
$x = 15^\circ$
代入 $x = 15^\circ$,得到三个内角的度数分别为:
$2x = 30^\circ$
$3x = 45^\circ$
$7x = 105^\circ$
由于 $105^\circ$ 是钝角,因此这个三角形是钝角三角形。
【答案】:D
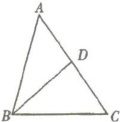
2. 如右图所示,在$\triangle ABC$中,$\angle A = 50^{\circ}$,$\angle ABC = 70^{\circ}$,$BD平分\angle ABC$,则$\angle BDC$的度数是(
A.$85^{\circ}$
B.$80^{\circ}$
C.$75^{\circ}$
D.$70^{\circ}$
A
)
A.$85^{\circ}$
B.$80^{\circ}$
C.$75^{\circ}$
D.$70^{\circ}$
答案:
【解析】:在$\triangle ABC$中,已知$\angle A = 50^{\circ}$,$\angle ABC = 70^{\circ}$,根据三角形内角和为$180^{\circ}$,可得$\angle C=180^{\circ}-\angle A-\angle ABC=180^{\circ}-50^{\circ}-70^{\circ}=60^{\circ}$。
因为$BD$平分$\angle ABC$,所以$\angle DBC=\frac{1}{2}\angle ABC=\frac{1}{2}×70^{\circ}=35^{\circ}$。
在$\triangle BDC$中,根据三角形内角和为$180^{\circ}$,可得$\angle BDC=180^{\circ}-\angle DBC-\angle C=180^{\circ}-35^{\circ}-60^{\circ}=85^{\circ}$。
【答案】:A
因为$BD$平分$\angle ABC$,所以$\angle DBC=\frac{1}{2}\angle ABC=\frac{1}{2}×70^{\circ}=35^{\circ}$。
在$\triangle BDC$中,根据三角形内角和为$180^{\circ}$,可得$\angle BDC=180^{\circ}-\angle DBC-\angle C=180^{\circ}-35^{\circ}-60^{\circ}=85^{\circ}$。
【答案】:A
3. 一个三角形的两边长为 $3$ 和 $7$,且第三边为整数,这样的三角形的周长的最小值是(
A.$14$
B.$15$
C.$16$
D.$17$
B
)A.$14$
B.$15$
C.$16$
D.$17$
答案:
【解析】:
设三角形的第三边长为$x$,根据三角形的性质,两边之和大于第三边,两边之差小于第三边,所以有:
$7 - 3 < x < 7 + 3$
即
$4 < x < 10$
由于题目中给出第三边为整数,所以$x$的取值范围为$5, 6, 7, 8, 9$。
三角形的周长为三边之和,即
$l = 3 + 7 + x = 10 + x$
为了使周长最小,$x$应取最小值$5$,所以
$l_{\text{min}} = 10 + 5 = 15$
【答案】:B
设三角形的第三边长为$x$,根据三角形的性质,两边之和大于第三边,两边之差小于第三边,所以有:
$7 - 3 < x < 7 + 3$
即
$4 < x < 10$
由于题目中给出第三边为整数,所以$x$的取值范围为$5, 6, 7, 8, 9$。
三角形的周长为三边之和,即
$l = 3 + 7 + x = 10 + x$
为了使周长最小,$x$应取最小值$5$,所以
$l_{\text{min}} = 10 + 5 = 15$
【答案】:B
4. 如右图所示,$\triangle ABC和\triangle DEF$中,已知,$AB = DE$,$\angle A = \angle D$,再加下列哪个条件不能得到$\triangle ABC \cong \triangle DEF$.(
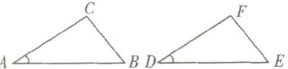
A.$AC = DF$
B.$\angle B = \angle E$
C.$\angle C = \angle F$
D.$BC = EF$
D
)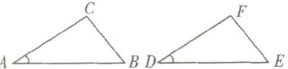
A.$AC = DF$
B.$\angle B = \angle E$
C.$\angle C = \angle F$
D.$BC = EF$
答案:
【解析】:
A. $AC=DF$,根据$SAS$(边角边)判定,两个三角形全等,故此选项不合题意;
B. $\angle B=\angle E$,根据$ASA$(角边角)判定,两个三角形全等,故此选项不合题意;
C. $\angle C=\angle F$,根据$AAS$(角角边)判定,两个三角形全等,故此选项不合题意;
D. $BC=EF$,这里只有两边和其中一边的对角对应相等,不能判定两个三角形全等,故此选项符合题意。
【答案】:D
A. $AC=DF$,根据$SAS$(边角边)判定,两个三角形全等,故此选项不合题意;
B. $\angle B=\angle E$,根据$ASA$(角边角)判定,两个三角形全等,故此选项不合题意;
C. $\angle C=\angle F$,根据$AAS$(角角边)判定,两个三角形全等,故此选项不合题意;
D. $BC=EF$,这里只有两边和其中一边的对角对应相等,不能判定两个三角形全等,故此选项符合题意。
【答案】:D
5. 关于三角形的角平分线,下列说法正确的是(
A.是线段
B.是射线
C.是直线
D.是射线或线段
A
)A.是线段
B.是射线
C.是直线
D.是射线或线段
答案:
【解析】:三角形的角平分线是指三角形一个内角的平分线与对边相交,这个角的顶点和交点之间的线段。根据线段的定义,线段有两个端点,而角平分线在三角形中具有明确的两个端点(角的顶点和与对边的交点),因此它是线段。射线有一个端点且向一方无限延伸,直线没有端点且向两方无限延伸,均不符合三角形角平分线的特征。
【答案】:A
【答案】:A
6. 如下图,$\triangle ABC \cong \triangle BAD$,$A$、$C$的对应点分别为点 $B$、$D$,若 $AB = 7cm$,$BC = 12cm$,$AC = 9cm$,那么 $BD$ 长是(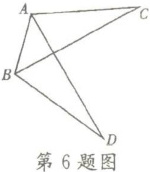
A.$7cm$
B.$9cm$
C.$12cm$
D.无法确定
B
)
A.$7cm$
B.$9cm$
C.$12cm$
D.无法确定
答案:
【解析】:
由于$\triangle ABC\cong\triangle BAD$,且$A,C$的对应点分别为$B,D$,
所以对应边$BD$和$AC$相等。
已知$AC=9$cm,
所以$BD=9$cm。
【答案】:B
由于$\triangle ABC\cong\triangle BAD$,且$A,C$的对应点分别为$B,D$,
所以对应边$BD$和$AC$相等。
已知$AC=9$cm,
所以$BD=9$cm。
【答案】:B
7. 如上图所示,$\triangle ACB \cong \triangle A'CB'$,$\angle BCB' = 30^{\circ}$,$\angle ACA'$的度数为(
A.$20^{\circ}$
B.$30^{\circ}$
C.$35^{\circ}$
D.$40^{\circ}$
B
)A.$20^{\circ}$
B.$30^{\circ}$
C.$35^{\circ}$
D.$40^{\circ}$
答案:
【解析】:因为△ACB≌△A'CB',所以∠ACB=∠A'CB'。等式两边同时减去∠A'CB,可得∠ACB - ∠A'CB = ∠A'CB' - ∠A'CB,即∠ACA' = ∠BCB'。已知∠BCB' = 30°,所以∠ACA' = 30°。
【答案】:B
【答案】:B
8. 利用基本作图,不能作出唯一三角形的是(
A.已知三边
B.已知两边及其夹角
C.已知两角及其夹边
D.已知两边及其中一边的对角
D
)A.已知三边
B.已知两边及其夹角
C.已知两角及其夹边
D.已知两边及其中一边的对角
答案:
【解析】:
A. 已知三边作三角形,根据$SSS$(边边边)全等条件,只要三边长度确定,就可以作出唯一的三角形。
B. 已知两边及其夹角作三角形,根据$SAS$(边角边)全等条件,只要两边长度和它们之间的夹角确定,就可以作出唯一的三角形。
C. 已知两角及其夹边作三角形,根据$ASA$(角边角)全等条件,只要两角大小和它们之间的夹边长度确定,就可以作出唯一的三角形。
D. 已知两边及其中一边的对角作三角形,这种情况不能根据现有的全等条件($SSS, SAS, ASA, AAS$等)作出唯一的三角形。因为即使两边长度和一个非夹角的角度确定,也不能保证作出的三角形是唯一的。
【答案】:D
A. 已知三边作三角形,根据$SSS$(边边边)全等条件,只要三边长度确定,就可以作出唯一的三角形。
B. 已知两边及其夹角作三角形,根据$SAS$(边角边)全等条件,只要两边长度和它们之间的夹角确定,就可以作出唯一的三角形。
C. 已知两角及其夹边作三角形,根据$ASA$(角边角)全等条件,只要两角大小和它们之间的夹边长度确定,就可以作出唯一的三角形。
D. 已知两边及其中一边的对角作三角形,这种情况不能根据现有的全等条件($SSS, SAS, ASA, AAS$等)作出唯一的三角形。因为即使两边长度和一个非夹角的角度确定,也不能保证作出的三角形是唯一的。
【答案】:D
9. 两个三角形的两条边及其中一条边的对角对应相等,下面四种说法中,正确的是(
(1) 这两个三角形全等;(2) 这两个三角形不全等;(3) 相等的两个角为锐角时,这两个三角形全等;(4) 相等的角是直角时,这两个三角形全等
A.$1$ 种
B.$2$ 种
C.$3$ 种
D.$4$ 种
4
)(1) 这两个三角形全等;(2) 这两个三角形不全等;(3) 相等的两个角为锐角时,这两个三角形全等;(4) 相等的角是直角时,这两个三角形全等
A.$1$ 种
B.$2$ 种
C.$3$ 种
D.$4$ 种
答案:
【解析】:
对于两个三角形的两条边及其中一条边的对角对应相等的情况,我们需要分析以下几种可能性:
(1) 这两个三角形全等:
仅根据两条边和其中一条边的对角对应相等,并不能确定两个三角形全等。因为三角形的形状不仅由边和角决定,还受到其他边和角的影响。
(2) 这两个三角形不全等:
这个说法也不能一概而论,因为在某些特殊情况下(如相等的角是直角),两个三角形可能是全等的。
(3) 相等的两个角为锐角时,这两个三角形全等:
当相等的两个角为锐角时,不能确保两个三角形全等。因为即使两个锐角相等,第三个角和边可能不同,导致三角形形状不同。
(4) 相等的角是直角时,这两个三角形全等:
当相等的角是直角,并且两条边对应相等时(即HL全等条件或SAS全等条件的一个特例),两个三角形是全等的。
综合以上分析,只有说法
(4)是正确的。
【答案】:A
对于两个三角形的两条边及其中一条边的对角对应相等的情况,我们需要分析以下几种可能性:
(1) 这两个三角形全等:
仅根据两条边和其中一条边的对角对应相等,并不能确定两个三角形全等。因为三角形的形状不仅由边和角决定,还受到其他边和角的影响。
(2) 这两个三角形不全等:
这个说法也不能一概而论,因为在某些特殊情况下(如相等的角是直角),两个三角形可能是全等的。
(3) 相等的两个角为锐角时,这两个三角形全等:
当相等的两个角为锐角时,不能确保两个三角形全等。因为即使两个锐角相等,第三个角和边可能不同,导致三角形形状不同。
(4) 相等的角是直角时,这两个三角形全等:
当相等的角是直角,并且两条边对应相等时(即HL全等条件或SAS全等条件的一个特例),两个三角形是全等的。
综合以上分析,只有说法
(4)是正确的。
【答案】:A
10. 如右图所示,要用“SAS”证$\triangle ABC \cong \triangle ADE$,若已知 $AB = AD$,$AC = AE$,则还需(
A.$\angle B = \angle D$
B.$\angle C = \angle E$
C.$\angle 1 = \angle 2$
D.$\angle 3 = \angle 4$
C
)
A.$\angle B = \angle D$
B.$\angle C = \angle E$
C.$\angle 1 = \angle 2$
D.$\angle 3 = \angle 4$
答案:
【解析】:
根据三角形全等(SAS)判定定理:两边及其夹角对应相等的三角形是全等三角形。
已知$AB=AD$,$AC=AE$,要使$\triangle ABC\cong\triangle ADE$,还需要这两组对应边的夹角相等。
在$\triangle ABC$和$\triangle ADE$中,$AB$与$AC$的夹角是$\angle BAC$,$AD$与$AE$的夹角是$\angle DAE$。
观察图形可知$\angle BAC=\angle 1+\angle 3$,$\angle DAE=\angle 2+\angle 3$。
若$\angle 1 = \angle 2$,则$\angle BAC=\angle DAE$,满足两边及其夹角对应相等,能根据“SAS”判定$\triangle ABC\cong\triangle ADE$。
选项A中$\angle B = \angle D$,是两边$AB = AD$与$AE = AC$的非夹角相等,不能根据“SAS”判定全等;
选项B中$\angle C = \angle E$,同样是两边$AB = AD$与$AE = AC$的非夹角相等,不能根据“SAS”判定全等;
选项D中$\angle 3 = \angle 4$,不是$AB$与$AC$、$AD$与$AE$的夹角相等,不能根据“SAS”判定全等。
【答案】:C
根据三角形全等(SAS)判定定理:两边及其夹角对应相等的三角形是全等三角形。
已知$AB=AD$,$AC=AE$,要使$\triangle ABC\cong\triangle ADE$,还需要这两组对应边的夹角相等。
在$\triangle ABC$和$\triangle ADE$中,$AB$与$AC$的夹角是$\angle BAC$,$AD$与$AE$的夹角是$\angle DAE$。
观察图形可知$\angle BAC=\angle 1+\angle 3$,$\angle DAE=\angle 2+\angle 3$。
若$\angle 1 = \angle 2$,则$\angle BAC=\angle DAE$,满足两边及其夹角对应相等,能根据“SAS”判定$\triangle ABC\cong\triangle ADE$。
选项A中$\angle B = \angle D$,是两边$AB = AD$与$AE = AC$的非夹角相等,不能根据“SAS”判定全等;
选项B中$\angle C = \angle E$,同样是两边$AB = AD$与$AE = AC$的非夹角相等,不能根据“SAS”判定全等;
选项D中$\angle 3 = \angle 4$,不是$AB$与$AC$、$AD$与$AE$的夹角相等,不能根据“SAS”判定全等。
【答案】:C
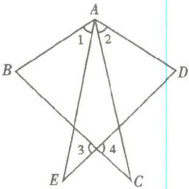
11. 如下图所示,以$\angle A$为一个内角的三角形有
3
个,它们是△ABC、△ADC、△AEB
,以 $BC$ 为一边的三角形有2
,它们是△ABC、△DBC
.
答案:
【解析】:以∠A为一个内角的三角形,需要找出所有包含顶点A的三角形。观察图形可知,包含顶点A的三角形有△ABC、△ADC、△AEB。共3个。
以BC为一边的三角形,需要找出所有包含线段BC的三角形。观察图形可知,包含线段BC的三角形有△ABC、△DBC。
【答案】:3;△ABC、△ADC、△AEB;2;△ABC、△DBC
以BC为一边的三角形,需要找出所有包含线段BC的三角形。观察图形可知,包含线段BC的三角形有△ABC、△DBC。
【答案】:3;△ABC、△ADC、△AEB;2;△ABC、△DBC
12. 如上图所示,点 $D$、$B$、$C$ 在同一直线上,$\angle A = 60^{\circ}$,$\angle C = 50^{\circ}$,$\angle D = 25^{\circ}$,则$\angle 1 = $
45
.
答案:
【解析】:在△ABC中,已知∠A=60°,∠C=50°,根据三角形内角和定理,∠ABC=180°-∠A-∠C=180°-60°-50°=70°。因为点D、B、C在同一直线上,所以∠ABC与∠ABD互为邻补角,即∠ABD=180°-∠ABC=180°-70°=110°。在△BDE中,已知∠D=25°,∠ABD=110°(即∠DBE=110°),根据三角形内角和定理,∠1=180°-∠D-∠DBE=180°-25°-110°=45°。
【答案】:45
【答案】:45
查看更多完整答案,请扫码查看


