2025年复习大本营期末假期复习一本通暑假八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年复习大本营期末假期复习一本通暑假八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
7. 洗衣机在洗
根据图象解答下列问题:
(1)洗衣机的进水时间是多少?清洗时洗衣机中的水量是多少?
(2)已知洗衣机的排水速度为19L/min,如果排水时间为2min,求排水结束时洗衣机中剩下的水量.
涤
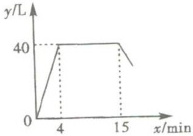
衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中水量y(L)与时间x(min)之间的关系如下图所示.根据图象解答下列问题:
(1)洗衣机的进水时间是多少?清洗时洗衣机中的水量是多少?
(2)已知洗衣机的排水速度为19L/min,如果排水时间为2min,求排水结束时洗衣机中剩下的水量.

答案:
【解析】:
(1)从图中可以看出,洗衣机的进水时间是$x=4$分钟,此时水量达到$40$升,并且在$4$到$15$分钟之间水量保持不变。因此,进水时间是$4$分钟,清洗时洗衣机中的水量是$40$升。
(2)已知洗衣机的排水速度为$19$升/分钟,排水时间为$2$分钟,
则排水量为$19 × 2=38$升。
排水开始时洗衣机中的水量为$40$升,
所以排水结束时洗衣机中剩下的水量为$40-38=2$升。
【答案】:
(1)洗衣机的进水时间是$4$分钟,清洗时洗衣机中的水量是$40$升。
(2)排水结束时洗衣机中剩下的水量为$2$升。
(1)从图中可以看出,洗衣机的进水时间是$x=4$分钟,此时水量达到$40$升,并且在$4$到$15$分钟之间水量保持不变。因此,进水时间是$4$分钟,清洗时洗衣机中的水量是$40$升。
(2)已知洗衣机的排水速度为$19$升/分钟,排水时间为$2$分钟,
则排水量为$19 × 2=38$升。
排水开始时洗衣机中的水量为$40$升,
所以排水结束时洗衣机中剩下的水量为$40-38=2$升。
【答案】:
(1)洗衣机的进水时间是$4$分钟,清洗时洗衣机中的水量是$40$升。
(2)排水结束时洗衣机中剩下的水量为$2$升。
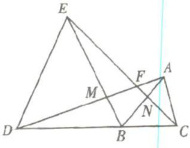
8. 如图所示,A,B,C,D,E,F,M,N是某公园的8个独立的景点,D,E,B三个景点相互之间距离相等;A,B,C三个景点相互之间距离相等.其中D,B,C三个景点在同一直线上,E,F,N,C四个景点在同一直线上,D,M,F,A四个景点也在同一直线上.游客甲从点E出发,沿E→F→N→C→A→B→M游览,游客乙从D点出发,沿D→M→F→A→C→B→N游览.若两人的速度相同,且在各景点游览的时间相同,试问甲、乙两人谁先游览完?试说明理由.

答案:
【解析】:
由题意知$DB = BE = DE$,$AB = BC = AC$,
所以$\bigtriangleup DEB$和$\bigtriangleup ABC$都是等边三角形,
所以$\angle DBE = \angle ABC = 60^{\circ}$,
因为$D$,$B$,$C$在同一直线上,
所以$\angle EBC = 180^{\circ} - \angle DBE = 120^{\circ}$,$\angle DBA = \angle DBC - \angle ABC = 60^{\circ}$,
所以$\angle EBC + \angle ABC = 180^{\circ}$,$\angle DBA = \angle ABC = 60^{\circ}$,
又因为$EB = AB$,$BC = BC$,
根据三角形全等(SAS)判定定理:两边及其夹角对应相等的三角形是全等三角形,
所以$\bigtriangleup EBC\cong \bigtriangleup ABC$,
所以$EC = AC$,$\angle BEC = \angle BAC = 30^{\circ}$,
所以$\angle ECA = \angle EAB = \angle ACE - \angle ACB = 30^{\circ}$,
即$\angle ECA = \angle BAC$,
所以$AE = EC$,
同理可证$\bigtriangleup DBC\cong \bigtriangleup FBC$,
所以$DF = FC$,
因为$D$,$M$,$F$,$A$在同一直线上,
所以$DA = DF + FA = \frac{1}{2}EC + FA = \frac{1}{2}AC + FA = FA + \frac{1}{2}(AB + BC)= FA + AB = MA + AB$,
即$DA = MB$,
同理可证$EN = AN$,
因为甲游客所走路线为$E→F→N→C→A→B→M$,
其总路程为:$EF + FN + NC + CA + AB + BM$,
乙游客所走路线为$D→M→F→A→C→B→N$,
其总路程为:$DM + MF + FA + AC + CB + BN$,
因为$EF + FN = DM + MF$(由$\bigtriangleup EBC\cong \bigtriangleup ABC$和$\bigtriangleup DBC\cong \bigtriangleup FBC$可推出相关线段关系),$NC = BN$(由$\bigtriangleup EBC\cong \bigtriangleup ABC$可得$BN = NC$),$CA = AC$,$AB = CB$,$BM = DA - AB = (MF + FA + AC)- AB = (MF + FA + AB)- AB = MF + FA$(这里用到了前面的结论$DA = MB$和$AC = AB + BC$),
所以两人的游览路程相同,
因为两人的速度相同,且在各景点游览的时间相同,
所以甲、乙两人同时游览完。
【答案】:甲、乙两人同时游览完。
由题意知$DB = BE = DE$,$AB = BC = AC$,
所以$\bigtriangleup DEB$和$\bigtriangleup ABC$都是等边三角形,
所以$\angle DBE = \angle ABC = 60^{\circ}$,
因为$D$,$B$,$C$在同一直线上,
所以$\angle EBC = 180^{\circ} - \angle DBE = 120^{\circ}$,$\angle DBA = \angle DBC - \angle ABC = 60^{\circ}$,
所以$\angle EBC + \angle ABC = 180^{\circ}$,$\angle DBA = \angle ABC = 60^{\circ}$,
又因为$EB = AB$,$BC = BC$,
根据三角形全等(SAS)判定定理:两边及其夹角对应相等的三角形是全等三角形,
所以$\bigtriangleup EBC\cong \bigtriangleup ABC$,
所以$EC = AC$,$\angle BEC = \angle BAC = 30^{\circ}$,
所以$\angle ECA = \angle EAB = \angle ACE - \angle ACB = 30^{\circ}$,
即$\angle ECA = \angle BAC$,
所以$AE = EC$,
同理可证$\bigtriangleup DBC\cong \bigtriangleup FBC$,
所以$DF = FC$,
因为$D$,$M$,$F$,$A$在同一直线上,
所以$DA = DF + FA = \frac{1}{2}EC + FA = \frac{1}{2}AC + FA = FA + \frac{1}{2}(AB + BC)= FA + AB = MA + AB$,
即$DA = MB$,
同理可证$EN = AN$,
因为甲游客所走路线为$E→F→N→C→A→B→M$,
其总路程为:$EF + FN + NC + CA + AB + BM$,
乙游客所走路线为$D→M→F→A→C→B→N$,
其总路程为:$DM + MF + FA + AC + CB + BN$,
因为$EF + FN = DM + MF$(由$\bigtriangleup EBC\cong \bigtriangleup ABC$和$\bigtriangleup DBC\cong \bigtriangleup FBC$可推出相关线段关系),$NC = BN$(由$\bigtriangleup EBC\cong \bigtriangleup ABC$可得$BN = NC$),$CA = AC$,$AB = CB$,$BM = DA - AB = (MF + FA + AC)- AB = (MF + FA + AB)- AB = MF + FA$(这里用到了前面的结论$DA = MB$和$AC = AB + BC$),
所以两人的游览路程相同,
因为两人的速度相同,且在各景点游览的时间相同,
所以甲、乙两人同时游览完。
【答案】:甲、乙两人同时游览完。
查看更多完整答案,请扫码查看


