2025年复习大本营期末假期复习一本通暑假八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年复习大本营期末假期复习一本通暑假八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
【针对训练2】如图所示的图形中,$\angle 1与\angle 2$互为邻补角的是(

D
)
答案:
【解析】:邻补角需要满足两个条件:一是有公共顶点和一条公共边,二是另一边互为反向延长线,两角之和为180°。
选项A:∠1与∠2有公共顶点和一条公共边,但另一边未互为反向延长线,不是邻补角。
选项B:∠1与∠2的边未形成互为反向延长线,且位置关系不符合邻补角定义,不是邻补角。
选项C:∠1与∠2是对顶角,对顶角只有公共顶点,没有公共边,不符合邻补角条件。
选项D:∠1与∠2有公共顶点、一条公共边,另一边互为反向延长线,满足邻补角定义。
【答案】:D
选项A:∠1与∠2有公共顶点和一条公共边,但另一边未互为反向延长线,不是邻补角。
选项B:∠1与∠2的边未形成互为反向延长线,且位置关系不符合邻补角定义,不是邻补角。
选项C:∠1与∠2是对顶角,对顶角只有公共顶点,没有公共边,不符合邻补角条件。
选项D:∠1与∠2有公共顶点、一条公共边,另一边互为反向延长线,满足邻补角定义。
【答案】:D
例3 下列说法中正确的是(
A.不相交的两条直线是平行线
B.同一个平面内,不相交的两条射线叫做平行线
C.同一个平面内,两条直线不相交就重合
D.同一个平面内,没有公共点的两条直线是平行线
D
)A.不相交的两条直线是平行线
B.同一个平面内,不相交的两条射线叫做平行线
C.同一个平面内,两条直线不相交就重合
D.同一个平面内,没有公共点的两条直线是平行线
答案:
【解析】:对于选项A,它忽略了“在同一平面内”的条件,如果两直线不在同一平面内,即使它们不相交,也不能称为平行线。因此,A选项是错误的。
对于选项B,平行线的定义是针对直线而言的,射线有一个端点,不能无限延伸,所以不能说两条射线不相交就是平行线。因此,B选项是错误的。
对于选项C,它忽略了平行线的可能性,即两条直线在同一平面内既不相交也不重合时,它们应该是平行的。因此,C选项是错误的。
对于选项D,它完全符合平行线的定义:在同一平面内,不相交的两条直线称为平行线。因此,D选项是正确的。
【答案】:D
对于选项B,平行线的定义是针对直线而言的,射线有一个端点,不能无限延伸,所以不能说两条射线不相交就是平行线。因此,B选项是错误的。
对于选项C,它忽略了平行线的可能性,即两条直线在同一平面内既不相交也不重合时,它们应该是平行的。因此,C选项是错误的。
对于选项D,它完全符合平行线的定义:在同一平面内,不相交的两条直线称为平行线。因此,D选项是正确的。
【答案】:D
【针对训练3】下列说法中,正确的是(
A.不相交的两条直线必定平行
B.两条直线的位置关系分为相交、平行、垂直
C.在同一平面内,不相交的两条射线必定平行
D.在同一平面内,不平行的两条直线必相交
D
)A.不相交的两条直线必定平行
B.两条直线的位置关系分为相交、平行、垂直
C.在同一平面内,不相交的两条射线必定平行
D.在同一平面内,不平行的两条直线必相交
答案:
【解析】:
A选项:不相交的两条直线必定平行。这一说法是不准确的,因为两条直线可能不在同一平面内,即使它们不相交,也不能说它们一定平行。故A选项错误。
B选项:两条直线的位置关系分为相交、平行、垂直。这一说法也是不准确的。在同一平面内,两条直线的位置关系只有相交和平行两种,垂直是相交的一种特殊情况。故B选项错误。
C选项:在同一平面内,不相交的两条射线必定平行。这一说法是错误的。射线有一个端点,即使两条射线不相交,由于射线的延伸性,也不能保证它们一定平行。故C选项错误。
D选项:在同一平面内,不平行的两条直线必相交。这一说法是正确的。在同一平面内,如果两条直线不平行,那么它们一定会在某一点相交。
【答案】:D
A选项:不相交的两条直线必定平行。这一说法是不准确的,因为两条直线可能不在同一平面内,即使它们不相交,也不能说它们一定平行。故A选项错误。
B选项:两条直线的位置关系分为相交、平行、垂直。这一说法也是不准确的。在同一平面内,两条直线的位置关系只有相交和平行两种,垂直是相交的一种特殊情况。故B选项错误。
C选项:在同一平面内,不相交的两条射线必定平行。这一说法是错误的。射线有一个端点,即使两条射线不相交,由于射线的延伸性,也不能保证它们一定平行。故C选项错误。
D选项:在同一平面内,不平行的两条直线必相交。这一说法是正确的。在同一平面内,如果两条直线不平行,那么它们一定会在某一点相交。
【答案】:D
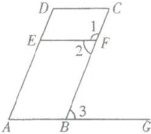
例4 根据右图,回答下列问题:
(1)由$\angle C= \angle 2$,可以判断哪两条直线平行?并说明理由。
(2)由$\angle 2= \angle 3$,可以判断哪两条直线平行?并说明理由。
(3)由$\angle D+\angle C= 180^{\circ}$,可以判断哪两条直线平行?并说明理由。
(1)由$\angle C= \angle 2$,可以判断哪两条直线平行?并说明理由。
(2)由$\angle 2= \angle 3$,可以判断哪两条直线平行?并说明理由。
(3)由$\angle D+\angle C= 180^{\circ}$,可以判断哪两条直线平行?并说明理由。

答案:
【解析】:
(1) 根据题意,$\angle C$ 和 $\angle 2$ 是直线 $DC$ 和 $EF$ 被直线 $CB$ 所截得的同位角。因为 $\angle C = \angle 2$,所以可以判断 $DC // EF$。理由是同位角相等,两直线平行。
(2) 根据题意,$\angle 2$ 和 $\angle 3$ 是直线 $EF$ 和 $AB$ 被直线 $CB$ 所截得的内错角。因为 $\angle 2 = \angle 3$,所以可以判断 $EF // AB$。理由是内错角相等,两直线平行。
(3) 根据题意,$\angle D$ 和 $\angle C$ 是直线 $AD$ 和 $BC$ 被直线 $DC$ 所截得的同旁内角。因为 $\angle D + \angle C = 180^\circ$,所以可以判断 $AD // BC$。理由是同旁内角互补,两直线平行。
【答案】:
(1) $DC // EF$
(2) $EF // AB$
(3) $AD // BC$
(1) 根据题意,$\angle C$ 和 $\angle 2$ 是直线 $DC$ 和 $EF$ 被直线 $CB$ 所截得的同位角。因为 $\angle C = \angle 2$,所以可以判断 $DC // EF$。理由是同位角相等,两直线平行。
(2) 根据题意,$\angle 2$ 和 $\angle 3$ 是直线 $EF$ 和 $AB$ 被直线 $CB$ 所截得的内错角。因为 $\angle 2 = \angle 3$,所以可以判断 $EF // AB$。理由是内错角相等,两直线平行。
(3) 根据题意,$\angle D$ 和 $\angle C$ 是直线 $AD$ 和 $BC$ 被直线 $DC$ 所截得的同旁内角。因为 $\angle D + \angle C = 180^\circ$,所以可以判断 $AD // BC$。理由是同旁内角互补,两直线平行。
【答案】:
(1) $DC // EF$
(2) $EF // AB$
(3) $AD // BC$
【针对训练4】如图所示,$\angle BDC= \angle ABD$,则在结论:①$\angle ADB= \angle CBD$;②$AB// CD$;③$AD// BC$中,正确的结论有(
A.$3$个
B.$2$个
C.$1$个
D.$0$个
C
)
A.$3$个
B.$2$个
C.$1$个
D.$0$个
答案:
【解析】:已知$\angle BDC = \angle ABD$,观察图形可知$\angle BDC$和$\angle ABD$是直线$AB$、$CD$被直线$BD$所截形成的内错角。根据内错角相等,两直线平行,可得出$AB// CD$,所以结论②正确。
对于结论①$\angle ADB = \angle CBD$,仅由$\angle BDC = \angle ABD$无法直接推出这两个角相等,缺少其他条件支持,所以①不一定正确。
对于结论③$AD// BC$,同样,仅已知$\angle BDC = \angle ABD$,无法得出$AD$与$BC$平行,没有相应的角关系或边关系作为依据,所以③错误。
综上,正确的结论只有②,共1个。
【答案】:C
对于结论①$\angle ADB = \angle CBD$,仅由$\angle BDC = \angle ABD$无法直接推出这两个角相等,缺少其他条件支持,所以①不一定正确。
对于结论③$AD// BC$,同样,仅已知$\angle BDC = \angle ABD$,无法得出$AD$与$BC$平行,没有相应的角关系或边关系作为依据,所以③错误。
综上,正确的结论只有②,共1个。
【答案】:C
例5 下列说法错误的是(
A.两直线平行,同位角相等
B.同位角相等,两直线平行
C.两直线平行,同旁内角相等
D.两直线平行,内错角相等
【剖析】三条性质中,只有同旁内角是互补的,其余两种的角均为相等关系,注意应避免弄混。此外,学习了平行线的识别和性质之后,要注意区分它们的区别与联系,关键是弄清条件和结论。
【解答】C
C
)A.两直线平行,同位角相等
B.同位角相等,两直线平行
C.两直线平行,同旁内角相等
D.两直线平行,内错角相等
【剖析】三条性质中,只有同旁内角是互补的,其余两种的角均为相等关系,注意应避免弄混。此外,学习了平行线的识别和性质之后,要注意区分它们的区别与联系,关键是弄清条件和结论。
【解答】C
答案:
【解析】:根据平行线的性质,当两直线平行时,同位角相等,内错角相等,同旁内角互补。
A选项表示两直线平行时,同位角相等,这是正确的;
B选项表示当同位角相等时,两直线平行,这也是平行线的一个判定定理,所以是正确的;
D选项表示两直线平行时,内错角相等,这是正确的;
而C选项表示两直线平行时,同旁内角相等,这是错误的,因为两直线平行时,同旁内角应该是互补的,不是相等的。
【答案】:C
A选项表示两直线平行时,同位角相等,这是正确的;
B选项表示当同位角相等时,两直线平行,这也是平行线的一个判定定理,所以是正确的;
D选项表示两直线平行时,内错角相等,这是正确的;
而C选项表示两直线平行时,同旁内角相等,这是错误的,因为两直线平行时,同旁内角应该是互补的,不是相等的。
【答案】:C
【针对训练5】如图所示,若直线$AB// CD$,则下面结论成立的是(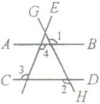
A.$\angle 1= \angle 4$
B.$\angle 2= \angle 3$
C.$\angle 2= \angle 4$
D.$\angle 3= \angle 4$
D
)
A.$\angle 1= \angle 4$
B.$\angle 2= \angle 3$
C.$\angle 2= \angle 4$
D.$\angle 3= \angle 4$
答案:
【解析】:因为直线$AB// CD$,所以根据两直线平行,同位角相等,内错角相等,同旁内角互补来分析各选项。
选项A:$\angle1$和$\angle4$是对顶角,对顶角相等,与$AB// CD$无关,所以该选项结论成立,但不确定是否是题目考查的平行性质导致的。
选项B:$\angle2$和$\angle3$,由图可知$\angle2$与$\angle4$是对顶角,所以$\angle2 = \angle4$,又因为$AB// CD$,$\angle4$和$\angle3$是内错角,所以$\angle4=\angle3$,从而$\angle2=\angle3$,该选项结论成立。
选项C:$\angle2$和$\angle4$是对顶角,对顶角相等,与$AB// CD$无关,所以该选项结论成立,但同样不确定是否是题目考查的平行性质导致的。
选项D:$\angle3$和$\angle4$,因为$AB// CD$,它们是内错角,所以$\angle3 = \angle4$,该选项结论成立。
不过,题目问的是“若直线$AB// CD$,则下面结论成立的是”,需要根据平行线的性质得出的结论。$\angle1=\angle4$和$\angle2=\angle4$是对顶角相等,不是由平行得到的。$\angle2=\angle3$是因为$\angle2=\angle4$(对顶角)且$\angle4=\angle3$(内错角,由平行得),所以$\angle2=\angle3$是由平行间接得到;$\angle3=\angle4$是直接由平行得到的内错角相等。
观察图形,$\angle3$和$\angle4$是直线$AB$、$CD$被直线$GH$所截形成的内错角,根据两直线平行,内错角相等,可得$\angle3 = \angle4$,所以选项D正确。而选项B中$\angle2$和$\angle3$,$\angle2$是$\angle1$的邻补角,$\angle1$与$\angle3$是同位角,$AB// CD$可得$\angle1=\angle3$,$\angle2$与$\angle1$互补,所以$\angle2$与$\angle3$互补,不一定相等,之前分析有误。$\angle2$和$\angle3$实际上是同旁内角,应该互补,而不是相等,所以选项B错误。
综上,正确的是选项D。
【答案】:D
选项A:$\angle1$和$\angle4$是对顶角,对顶角相等,与$AB// CD$无关,所以该选项结论成立,但不确定是否是题目考查的平行性质导致的。
选项B:$\angle2$和$\angle3$,由图可知$\angle2$与$\angle4$是对顶角,所以$\angle2 = \angle4$,又因为$AB// CD$,$\angle4$和$\angle3$是内错角,所以$\angle4=\angle3$,从而$\angle2=\angle3$,该选项结论成立。
选项C:$\angle2$和$\angle4$是对顶角,对顶角相等,与$AB// CD$无关,所以该选项结论成立,但同样不确定是否是题目考查的平行性质导致的。
选项D:$\angle3$和$\angle4$,因为$AB// CD$,它们是内错角,所以$\angle3 = \angle4$,该选项结论成立。
不过,题目问的是“若直线$AB// CD$,则下面结论成立的是”,需要根据平行线的性质得出的结论。$\angle1=\angle4$和$\angle2=\angle4$是对顶角相等,不是由平行得到的。$\angle2=\angle3$是因为$\angle2=\angle4$(对顶角)且$\angle4=\angle3$(内错角,由平行得),所以$\angle2=\angle3$是由平行间接得到;$\angle3=\angle4$是直接由平行得到的内错角相等。
观察图形,$\angle3$和$\angle4$是直线$AB$、$CD$被直线$GH$所截形成的内错角,根据两直线平行,内错角相等,可得$\angle3 = \angle4$,所以选项D正确。而选项B中$\angle2$和$\angle3$,$\angle2$是$\angle1$的邻补角,$\angle1$与$\angle3$是同位角,$AB// CD$可得$\angle1=\angle3$,$\angle2$与$\angle1$互补,所以$\angle2$与$\angle3$互补,不一定相等,之前分析有误。$\angle2$和$\angle3$实际上是同旁内角,应该互补,而不是相等,所以选项B错误。
综上,正确的是选项D。
【答案】:D
查看更多完整答案,请扫码查看


