2025年复习大本营期末假期复习一本通暑假八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年复习大本营期末假期复习一本通暑假八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列说法中错误的是(
A.关于某条直线对称的两个图形一定能够完全重合
B.轴对称图形的对称轴至少有一条
C.两个全等的图形一定关于某条直线成轴对称
D.圆是轴对称图形
C
)A.关于某条直线对称的两个图形一定能够完全重合
B.轴对称图形的对称轴至少有一条
C.两个全等的图形一定关于某条直线成轴对称
D.圆是轴对称图形
答案:
【解析】:
A选项:关于某条直线对称的两个图形一定能够完全重合。这是轴对称的基本定义,即如果两个图形关于某条直线对称,那么它们一定能够完全重合。所以A选项是正确的。
B选项:轴对称图形的对称轴至少有一条。这也是轴对称图形的基本性质,即它至少有一条对称轴使得图形关于这条轴对称。所以B选项是正确的。
C选项:两个全等的图形一定关于某条直线成轴对称。这个说法是错误的。两个全等的图形仅仅说明它们的形状和大小完全相同,但并不意味着它们一定关于某条直线成轴对称。例如,我们可以通过平移、旋转等方式得到两个全等的图形,但它们并不关于某条直线成轴对称。所以C选项是错误的。
D选项:圆是轴对称图形。这个说法是正确的,因为圆关于任意经过其圆心的直线都是对称的。
综上所述,错误的说法是C选项。
【答案】:C
A选项:关于某条直线对称的两个图形一定能够完全重合。这是轴对称的基本定义,即如果两个图形关于某条直线对称,那么它们一定能够完全重合。所以A选项是正确的。
B选项:轴对称图形的对称轴至少有一条。这也是轴对称图形的基本性质,即它至少有一条对称轴使得图形关于这条轴对称。所以B选项是正确的。
C选项:两个全等的图形一定关于某条直线成轴对称。这个说法是错误的。两个全等的图形仅仅说明它们的形状和大小完全相同,但并不意味着它们一定关于某条直线成轴对称。例如,我们可以通过平移、旋转等方式得到两个全等的图形,但它们并不关于某条直线成轴对称。所以C选项是错误的。
D选项:圆是轴对称图形。这个说法是正确的,因为圆关于任意经过其圆心的直线都是对称的。
综上所述,错误的说法是C选项。
【答案】:C
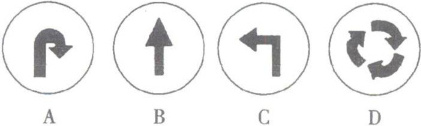
2. 下列图形中,是轴对称图形的是(
B
)
答案:
【解析】:
轴对称图形是指一个图形关于某条直线(称为对称轴)对称,如果沿这条直线折叠,图形的两部分能够完全重合。
A选项:图形是一个向右的弯曲箭头,找不到一条直线使其对称,不是轴对称图形。
B选项:图形是一个向上的箭头,可以找到一条垂直的对称轴,使其沿对称轴折叠后完全重合,是轴对称图形。
C选项:图形是一个向左的弯折箭头,找不到一条直线使其对称,不是轴对称图形。
D选项:图形是一个循环箭头,找不到一条直线使其对称,不是轴对称图形。
【答案】:B
轴对称图形是指一个图形关于某条直线(称为对称轴)对称,如果沿这条直线折叠,图形的两部分能够完全重合。
A选项:图形是一个向右的弯曲箭头,找不到一条直线使其对称,不是轴对称图形。
B选项:图形是一个向上的箭头,可以找到一条垂直的对称轴,使其沿对称轴折叠后完全重合,是轴对称图形。
C选项:图形是一个向左的弯折箭头,找不到一条直线使其对称,不是轴对称图形。
D选项:图形是一个循环箭头,找不到一条直线使其对称,不是轴对称图形。
【答案】:B
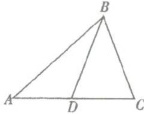
3. 如右图所示,$AB= AC$,$BD= BC$,若$∠A= 40^{\circ }$,则$∠ABD=$(
A.$20^{\circ }$
B.$30^{\circ }$
C.$35^{\circ }$
D.$40^{\circ }$
30°
)
A.$20^{\circ }$
B.$30^{\circ }$
C.$35^{\circ }$
D.$40^{\circ }$
答案:
【解析】:
因为$AB=AC$,$\angle A=40^\circ$,所以$\angle C=\angle ABC=(180^\circ-40^\circ)÷2=70^\circ$。
又因为$BD=BC$,所以$\angle BDC=\angle C=70^\circ$,
$\angle BDC$为$\triangle ABD$的外角,所以$\angle ABD=\angle BDC-\angle A=70^\circ-40^\circ=30^\circ$。
【答案】:B
因为$AB=AC$,$\angle A=40^\circ$,所以$\angle C=\angle ABC=(180^\circ-40^\circ)÷2=70^\circ$。
又因为$BD=BC$,所以$\angle BDC=\angle C=70^\circ$,
$\angle BDC$为$\triangle ABD$的外角,所以$\angle ABD=\angle BDC-\angle A=70^\circ-40^\circ=30^\circ$。
【答案】:B
4. 下列说法:①关于某条直线对称的两条线段相等;②相等的两条线段一定关于某条直线对称;③线段AB的对称轴是经过线段AB中点的一条直线;④线段AB的对称轴是线段AB的垂直平分线。其中正确的是(
A.①②③④
B.①③④
C.②③④
D.①④
D
)A.①②③④
B.①③④
C.②③④
D.①④
答案:
【解析】:
① 关于某条直线对称的两条线段相等:这是正确的。如果两条线段关于某条直线对称,那么它们一定是相等的。
② 相等的两条线段一定关于某条直线对称:这是错误的。两条线段相等,并不意味着它们一定关于某条直线对称。例如,两条长度相等但方向完全不同的线段就不关于任何直线对称。
③ 线段AB的对称轴是经过线段AB中点的一条直线:这是不准确的。经过线段AB中点的直线有很多,但只有垂直于线段AB且经过其中点的那条直线才是其对称轴。
④ 线段AB的对称轴是线段AB的垂直平分线:这是正确的。线段AB的垂直平分线正是其对称轴。
【答案】:D
① 关于某条直线对称的两条线段相等:这是正确的。如果两条线段关于某条直线对称,那么它们一定是相等的。
② 相等的两条线段一定关于某条直线对称:这是错误的。两条线段相等,并不意味着它们一定关于某条直线对称。例如,两条长度相等但方向完全不同的线段就不关于任何直线对称。
③ 线段AB的对称轴是经过线段AB中点的一条直线:这是不准确的。经过线段AB中点的直线有很多,但只有垂直于线段AB且经过其中点的那条直线才是其对称轴。
④ 线段AB的对称轴是线段AB的垂直平分线:这是正确的。线段AB的垂直平分线正是其对称轴。
【答案】:D
5. 下列图形不是轴对称图形的是(
A.有一个角为钝角的等腰三角形
B.有一个角为$45^{\circ }$的直角三角形
C.有一个角为$60^{\circ }$的等腰三角形
D.有一个角为$40^{\circ }$的直角三角形
D
)A.有一个角为钝角的等腰三角形
B.有一个角为$45^{\circ }$的直角三角形
C.有一个角为$60^{\circ }$的等腰三角形
D.有一个角为$40^{\circ }$的直角三角形
答案:
【解析】:轴对称图形是指沿一条直线折叠后,直线两旁的部分能够完全重合的图形。
选项A:有一个角为钝角的等腰三角形,其钝角只能是顶角,两底角相等,等腰三角形是轴对称图形,对称轴为底边上的高(或顶角平分线、底边中线),所以该图形是轴对称图形。
选项B:有一个角为$45^{\circ}$的直角三角形,另一个锐角为$180^{\circ}-90^{\circ}-45^{\circ}=45^{\circ}$,此三角形为等腰直角三角形,等腰三角形是轴对称图形,对称轴为斜边的高(或斜边中线、直角的平分线),所以该图形是轴对称图形。
选项C:有一个角为$60^{\circ}$的等腰三角形,若顶角为$60^{\circ}$,则两底角均为$(180^{\circ}-60^{\circ})÷2 = 60^{\circ}$;若底角为$60^{\circ}$,则顶角为$180^{\circ}-60^{\circ}×2=60^{\circ}$,所以该三角形是等边三角形,等边三角形是特殊的等腰三角形,是轴对称图形,有三条对称轴,所以该图形是轴对称图形。
选项D:有一个角为$40^{\circ}$的直角三角形,另一个锐角为$180^{\circ}-90^{\circ}-40^{\circ}=50^{\circ}$,三个角分别为$90^{\circ}$、$40^{\circ}$、$50^{\circ}$,三条边互不相等(直角三角形中斜边最长,两直角边不相等),不是等腰三角形,所以不是轴对称图形。
【答案】:D
选项A:有一个角为钝角的等腰三角形,其钝角只能是顶角,两底角相等,等腰三角形是轴对称图形,对称轴为底边上的高(或顶角平分线、底边中线),所以该图形是轴对称图形。
选项B:有一个角为$45^{\circ}$的直角三角形,另一个锐角为$180^{\circ}-90^{\circ}-45^{\circ}=45^{\circ}$,此三角形为等腰直角三角形,等腰三角形是轴对称图形,对称轴为斜边的高(或斜边中线、直角的平分线),所以该图形是轴对称图形。
选项C:有一个角为$60^{\circ}$的等腰三角形,若顶角为$60^{\circ}$,则两底角均为$(180^{\circ}-60^{\circ})÷2 = 60^{\circ}$;若底角为$60^{\circ}$,则顶角为$180^{\circ}-60^{\circ}×2=60^{\circ}$,所以该三角形是等边三角形,等边三角形是特殊的等腰三角形,是轴对称图形,有三条对称轴,所以该图形是轴对称图形。
选项D:有一个角为$40^{\circ}$的直角三角形,另一个锐角为$180^{\circ}-90^{\circ}-40^{\circ}=50^{\circ}$,三个角分别为$90^{\circ}$、$40^{\circ}$、$50^{\circ}$,三条边互不相等(直角三角形中斜边最长,两直角边不相等),不是等腰三角形,所以不是轴对称图形。
【答案】:D
6. 下列轴对称图形中对称轴最多的是(
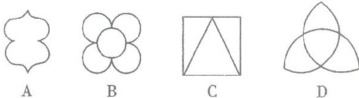
B
)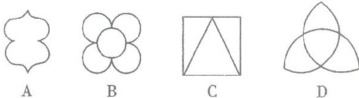
答案:
【解析】:
选项A:该图形有2条对称轴,即连接上下两个突出部分中点的直线和连接左右两个突出部分中点的直线。
选项B:该图形有6条对称轴,分别是通过每个花瓣中心与相邻花瓣中心连线的直线,共6条。
选项C:该图形有4条对称轴,分别是两条对角线和连接对边中点的两条直线。
选项D:该图形有3条对称轴,分别是通过每个顶点与对边中点的直线。
比较四个选项的对称轴数量,B选项的对称轴最多,有6条。
【答案】:B
选项A:该图形有2条对称轴,即连接上下两个突出部分中点的直线和连接左右两个突出部分中点的直线。
选项B:该图形有6条对称轴,分别是通过每个花瓣中心与相邻花瓣中心连线的直线,共6条。
选项C:该图形有4条对称轴,分别是两条对角线和连接对边中点的两条直线。
选项D:该图形有3条对称轴,分别是通过每个顶点与对边中点的直线。
比较四个选项的对称轴数量,B选项的对称轴最多,有6条。
【答案】:B
7. 已知平面上两点A、B,下列说法不正确的是(
A.点A,点B关于AB的中垂线对称
B.点A,点B可看作是以直线AB为对称轴的对应点
C.点A,点B是成轴对称的,且只有一条对称轴
D.点A,点B是轴对称图形,A,B是对应点
B
)A.点A,点B关于AB的中垂线对称
B.点A,点B可看作是以直线AB为对称轴的对应点
C.点A,点B是成轴对称的,且只有一条对称轴
D.点A,点B是轴对称图形,A,B是对应点
答案:
【解析】:对于选项A,AB的中垂线是线段AB的垂直平分线,根据垂直平分线的性质,线段垂直平分线上的点到线段两端距离相等,所以点A和点B关于AB的中垂线对称,该选项正确;
对于选项B,以直线AB为对称轴时,点A的对称点是它本身,点B的对称点也是它本身,所以点A和点B不能看作是以直线AB为对称轴的对应点(对应点应该是不同的点),该选项错误;
对于选项C,点A和点B成轴对称,对称轴是线段AB的垂直平分线,只有这一条对称轴,该选项正确;
对于选项D,两个点组成的图形是轴对称图形,对称轴是AB的中垂线,A和B是对应点,该选项正确。
【答案】:B
对于选项B,以直线AB为对称轴时,点A的对称点是它本身,点B的对称点也是它本身,所以点A和点B不能看作是以直线AB为对称轴的对应点(对应点应该是不同的点),该选项错误;
对于选项C,点A和点B成轴对称,对称轴是线段AB的垂直平分线,只有这一条对称轴,该选项正确;
对于选项D,两个点组成的图形是轴对称图形,对称轴是AB的中垂线,A和B是对应点,该选项正确。
【答案】:B
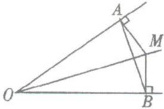
8. 如右图,已知$∠AOB= 40^{\circ }$,OM平分$∠AOB$,$AM⊥OA$于A,$MB⊥OB$于B,则$∠MAB$的度数为(
A.$50^{\circ }$
B.$40^{\circ }$
C.$30^{\circ }$
D.$20^{\circ }$
D
)
A.$50^{\circ }$
B.$40^{\circ }$
C.$30^{\circ }$
D.$20^{\circ }$
答案:
【解析】:
由于 $OM$ 平分 $\angle AOB$,所以 $\angle AOM = \angle BOM = \frac{1}{2} \angle AOB = \frac{1}{2} × 40^\circ = 20^\circ$。
$AM \perp OA$,所以 $\angle OAM = 90^\circ$。
$MB \perp OB$,所以 $\angle OBM = 90^\circ$。
在四边形 $OAMB$ 中,内角和为 $360^\circ$,
所以 $\angle AMB = 360^\circ - \angle OAM - \angle OBM - \angle AOB = 360^\circ - 90^\circ - 90^\circ - 40^\circ = 140^\circ$。
由于 $OM$ 是 $\angle AOB$ 的平分线,且 $AM \perp OA$,$MB \perp OB$,
所以 $\triangle OAM \cong \triangle OBM$(根据HL全等条件),
从而 $AM = BM$。
因此,$\triangle AMB$ 是等腰三角形,
所以 $\angle MAB = \frac{1}{2} (180^\circ - \angle AMB) = \frac{1}{2} (180^\circ - 140^\circ) = 20^\circ$。
【答案】:D
由于 $OM$ 平分 $\angle AOB$,所以 $\angle AOM = \angle BOM = \frac{1}{2} \angle AOB = \frac{1}{2} × 40^\circ = 20^\circ$。
$AM \perp OA$,所以 $\angle OAM = 90^\circ$。
$MB \perp OB$,所以 $\angle OBM = 90^\circ$。
在四边形 $OAMB$ 中,内角和为 $360^\circ$,
所以 $\angle AMB = 360^\circ - \angle OAM - \angle OBM - \angle AOB = 360^\circ - 90^\circ - 90^\circ - 40^\circ = 140^\circ$。
由于 $OM$ 是 $\angle AOB$ 的平分线,且 $AM \perp OA$,$MB \perp OB$,
所以 $\triangle OAM \cong \triangle OBM$(根据HL全等条件),
从而 $AM = BM$。
因此,$\triangle AMB$ 是等腰三角形,
所以 $\angle MAB = \frac{1}{2} (180^\circ - \angle AMB) = \frac{1}{2} (180^\circ - 140^\circ) = 20^\circ$。
【答案】:D
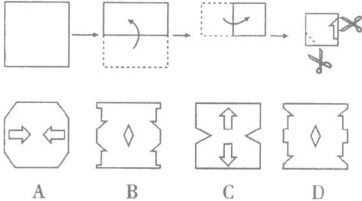
9. 如下图所示,将一个正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去一个三角形和一个形如“↑”的图形,将纸片展开,得到的图形是(
D
)
答案:
【解析】:我们按照折叠顺序逐步分析。首先,将正方形纸片向右折叠,此时右边部分覆盖在左边之上;接着向上折叠,下边部分又覆盖到上边;最后向右上方折叠,形成一个多层的小三角形区域。
在最后折叠好的纸片上,沿虚线剪去一个三角形和一个“↑”形图形。根据折叠的对称性,剪去的部分会在展开后的正方形纸片上形成相应的对称图案。当我们逐步展开纸片时,每一层折叠都会使剪去的部分在对应位置产生镜像。
对于剪去的三角形,由于经过多次折叠,展开后会在正方形的四个角附近形成对称的三角形缺口。而“↑”形图形,在折叠状态下剪去后,展开时会因为不同方向的折叠,形成上下两个方向相反的“↑”和“↓”组合,也就是类似“↕”的形状,且位于正方形的中间区域。
综合这些特征,对比各个选项,只有选项 D 符合上述分析的图形特征。
【答案】:D
在最后折叠好的纸片上,沿虚线剪去一个三角形和一个“↑”形图形。根据折叠的对称性,剪去的部分会在展开后的正方形纸片上形成相应的对称图案。当我们逐步展开纸片时,每一层折叠都会使剪去的部分在对应位置产生镜像。
对于剪去的三角形,由于经过多次折叠,展开后会在正方形的四个角附近形成对称的三角形缺口。而“↑”形图形,在折叠状态下剪去后,展开时会因为不同方向的折叠,形成上下两个方向相反的“↑”和“↓”组合,也就是类似“↕”的形状,且位于正方形的中间区域。
综合这些特征,对比各个选项,只有选项 D 符合上述分析的图形特征。
【答案】:D
10. 把一张正方形的白纸,沿对角线对折后,得到一个等腰直角三角形,再沿高折叠后又得到一个更小的等腰直角三角形,在重叠的这张纸上剪出一个花纹,打开纸后得到一个图案,该图案至少有(
A.1
B.2
C.3
D.4
2
)条对称轴。A.1
B.2
C.3
D.4
答案:
【解析】:
本题考察的是对折后图形的对称轴数量。
首先,我们明确对称轴的定义:一个图形关于某条直线对称,如果沿这条直线折叠,图形的两部分能够完全重合,那么这条直线就叫做这个图形的对称轴。
接下来,我们分析题目中的折叠过程:
1. 一张正方形的白纸,沿对角线对折后,得到一个等腰直角三角形。这个等腰直角三角形有一条对称轴,即其对角线(也是折叠线)。
2. 再沿高折叠后,得到一个更小的等腰直角三角形。此时,小等腰直角三角形依然关于其直角平分线(也是高,同时也是之前的折叠线的一部分)对称。但此时,由于纸张是重叠的,我们需要考虑的是整个重叠后的图形。
3. 在重叠的纸上剪出一个花纹,打开纸后,由于每次折叠都是关于某条直线对称的,所以剪出的花纹也会关于这些折叠线对称。
现在,我们考虑打开纸后的图案:
由于纸张首先沿对角线对折,然后再沿高对折,所以打开后的图案至少会保留这两条对称轴:一条是正方形的对角线,另一条是等腰直角三角形的高(也是正方形对角线的一部分,但在考虑整个图案时,它作为另一条独立的对称轴存在)。但实际上,由于正方形本身有两条对角线,且它们都是对称轴,而在本题中,由于折叠的方式,我们只需要考虑其中一条对角线和与这条对角线垂直的等腰直角三角形的高作为对称轴。然而,由于正方形的特性,与这条对角线垂直的另一条对角线(虽然不是折叠线,但在完整图案中也是对称轴)也会是图案的对称轴。但题目问的是“至少有”多少条对称轴,所以我们只需考虑由折叠直接产生的那两条。但在这里,我们需要注意到,由于正方形的四边等长,且对角线互相垂直平分,所以实际上打开后的图案关于正方形的两条对角线都是对称的。
因此,该图案至少有2条对称轴(即正方形的两条对角线)。但如果仅从折叠过程来看,我们“直接”得到的是一条对角线和一条高作为对称轴,但由于正方形的性质,另一条对角线也自然成为对称轴。所以,题目中的“至少”指的是在折叠过程中直接或间接产生的对称轴数量。
综上所述,答案是该图案至少有2条对称轴。
【答案】:B
本题考察的是对折后图形的对称轴数量。
首先,我们明确对称轴的定义:一个图形关于某条直线对称,如果沿这条直线折叠,图形的两部分能够完全重合,那么这条直线就叫做这个图形的对称轴。
接下来,我们分析题目中的折叠过程:
1. 一张正方形的白纸,沿对角线对折后,得到一个等腰直角三角形。这个等腰直角三角形有一条对称轴,即其对角线(也是折叠线)。
2. 再沿高折叠后,得到一个更小的等腰直角三角形。此时,小等腰直角三角形依然关于其直角平分线(也是高,同时也是之前的折叠线的一部分)对称。但此时,由于纸张是重叠的,我们需要考虑的是整个重叠后的图形。
3. 在重叠的纸上剪出一个花纹,打开纸后,由于每次折叠都是关于某条直线对称的,所以剪出的花纹也会关于这些折叠线对称。
现在,我们考虑打开纸后的图案:
由于纸张首先沿对角线对折,然后再沿高对折,所以打开后的图案至少会保留这两条对称轴:一条是正方形的对角线,另一条是等腰直角三角形的高(也是正方形对角线的一部分,但在考虑整个图案时,它作为另一条独立的对称轴存在)。但实际上,由于正方形本身有两条对角线,且它们都是对称轴,而在本题中,由于折叠的方式,我们只需要考虑其中一条对角线和与这条对角线垂直的等腰直角三角形的高作为对称轴。然而,由于正方形的特性,与这条对角线垂直的另一条对角线(虽然不是折叠线,但在完整图案中也是对称轴)也会是图案的对称轴。但题目问的是“至少有”多少条对称轴,所以我们只需考虑由折叠直接产生的那两条。但在这里,我们需要注意到,由于正方形的四边等长,且对角线互相垂直平分,所以实际上打开后的图案关于正方形的两条对角线都是对称的。
因此,该图案至少有2条对称轴(即正方形的两条对角线)。但如果仅从折叠过程来看,我们“直接”得到的是一条对角线和一条高作为对称轴,但由于正方形的性质,另一条对角线也自然成为对称轴。所以,题目中的“至少”指的是在折叠过程中直接或间接产生的对称轴数量。
综上所述,答案是该图案至少有2条对称轴。
【答案】:B
11. 底边长为2a,底角为$30^{\circ }$的等腰三角形,腰上的高为______
$\sqrt{3}a$
。
答案:
【解析】:已知等腰三角形底边长为$2a$,底角为$30^{\circ}$。我们可以通过作底边上的高,将等腰三角形分为两个全等的直角三角形。在其中一个直角三角形中,底角为$30^{\circ}$,对边为底边长的一半,即$a$。根据正弦函数的定义,$\sin30^{\circ}=\frac{对边}{斜边}=\frac{a}{腰长}$,因为$\sin30^{\circ}=\frac{1}{2}$,所以腰长为$2a$。
接下来求腰上的高。设腰上的高为$h$,根据三角形面积公式,三角形面积可以表示为$\frac{1}{2}×底×底边上的高$,也可以表示为$\frac{1}{2}×腰×腰上的高$。
先求底边上的高,在上述直角三角形中,根据勾股定理,底边上的高为$\sqrt{(2a)^2 - a^2}=\sqrt{3}a$,所以三角形面积为$\frac{1}{2}×2a×\sqrt{3}a=\sqrt{3}a^2$。
又因为面积也等于$\frac{1}{2}×腰× h=\frac{1}{2}×2a× h = ah$,所以$ah = \sqrt{3}a^2$,解得$h = \sqrt{3}a$。
【答案】:$\sqrt{3}a$
接下来求腰上的高。设腰上的高为$h$,根据三角形面积公式,三角形面积可以表示为$\frac{1}{2}×底×底边上的高$,也可以表示为$\frac{1}{2}×腰×腰上的高$。
先求底边上的高,在上述直角三角形中,根据勾股定理,底边上的高为$\sqrt{(2a)^2 - a^2}=\sqrt{3}a$,所以三角形面积为$\frac{1}{2}×2a×\sqrt{3}a=\sqrt{3}a^2$。
又因为面积也等于$\frac{1}{2}×腰× h=\frac{1}{2}×2a× h = ah$,所以$ah = \sqrt{3}a^2$,解得$h = \sqrt{3}a$。
【答案】:$\sqrt{3}a$
12. $△ABC$,$AB= AC$,BD是三角形的角平分线,$∠BDC= 75^{\circ }$,则$∠A= $______
40°
。
答案:
【解析】:设∠A的度数为x,因为AB=AC,所以△ABC是等腰三角形,∠ABC=∠ACB。根据三角形内角和定理,∠ABC=∠ACB=(180°-x)/2=90°-x/2。
BD是∠ABC的角平分线,所以∠ABD=∠DBC=(∠ABC)/2=(90°-x/2)/2=45°-x/4。
在△BDC中,∠BDC=75°,∠DBC=45°-x/4,∠ACB=90°-x/2(即∠BCD=90°-x/2)。根据三角形内角和定理可得:∠DBC+∠BCD+∠BDC=180°,即(45°-x/4)+(90°-x/2)+75°=180°。
化简方程:45°-x/4+90°-x/2+75°=180°,210°-(3x/4)=180°,3x/4=30°,x=40°。
【答案】:40°
BD是∠ABC的角平分线,所以∠ABD=∠DBC=(∠ABC)/2=(90°-x/2)/2=45°-x/4。
在△BDC中,∠BDC=75°,∠DBC=45°-x/4,∠ACB=90°-x/2(即∠BCD=90°-x/2)。根据三角形内角和定理可得:∠DBC+∠BCD+∠BDC=180°,即(45°-x/4)+(90°-x/2)+75°=180°。
化简方程:45°-x/4+90°-x/2+75°=180°,210°-(3x/4)=180°,3x/4=30°,x=40°。
【答案】:40°
13. 已知在$△ABC$中,$AB= AC$,且$∠B= \frac {1}{2}∠BAC$,则$∠B= $
45°
。
答案:
【解析】:因为在$△ABC$中,$AB = AC$,所以$△ABC$是等腰三角形,$∠B = ∠C$(等边对等角)。设$∠B = x$,已知$∠B = \frac{1}{2}∠BAC$,则$∠BAC = 2x$。由于三角形内角和为$180^{\circ}$,可得$∠BAC + ∠B + ∠C = 180^{\circ}$,即$2x + x + x = 180^{\circ}$,$4x = 180^{\circ}$,解得$x = 45^{\circ}$,所以$∠B = 45^{\circ}$。
【答案】:45°
【答案】:45°
查看更多完整答案,请扫码查看


