《2025年复习大本营期末假期复习一本通暑假八年级数学北师大版》

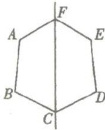
例3 如右图所示,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠BCF= 150°,则∠AFE+∠BCD的大小是(B)

A.150°
B.300°
C.210°
D.330°

答案： 【解析】：观察图形，且六边形ABCDEF是轴对称图形，CF所在的直线是它的对称轴，
利用轴对称图形的性质可知，
对应点所连的线段被对称轴垂直平分，对应角相等，
所以$\angle AFC=\angle CFE$，$\angle BCF=\angle FCD$，
因为$\angle AFC+\angle BCF=150^\circ$，
所以$\angle AFE+\angle BCD=(\angle AFC+\angle CFE)+(\angle BCF+\angle FCD)=2(\angle AFC+\angle BCF)=2×150^\circ=300^\circ$。
【答案】：B

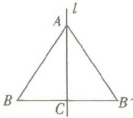
【针对训练3】 如右图所示,在Rt△ABC中,∠ACB= 90°,AB= 2BC,以直线AC所在直线l为对称轴,点B'是点B的对称点,则BC= ______$\frac{1}{2}AB$,AB的对应线段是______$AB'$,∠B的对应角是______$\angle B'$,△ABB'是______等边三角形,因此,∠BAB'的度数是______$60^{\circ}$,∠BAC的度数是______$30^{\circ}$。

答案： 【解析】：
因为$AB=2BC$，且在$Rt\triangle ABC$中，$\angle ACB = 90^{\circ}$，设$BC=x$，则$AB = 2x$，根据勾股定理$AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{(2x)^{2}-x^{2}}=\sqrt{3}x$，同时$\cos B=\frac{BC}{AB}=\frac{x}{2x}=\frac{1}{2}$，所以$\angle B = 60^{\circ}$，那么$\angle BAC=30^{\circ}$，又因为$AB = 2BC$，所以$BC = AC÷\sqrt{3}=\frac{\sqrt{3}}{3}AB÷\sqrt{3}=\frac{1}{2}AB$，即$BC=\frac{1}{2}AB$。
因为点$B$与点$B'$关于直线$l$对称，所以$AB$的对应线段是$AB'$，$\angle B$的对应角是$\angle B'$。
由于点$B$与点$B'$关于直线$AC$对称，所以$AB = AB'$，$\angle BAB' = 2\angle BAC$（对称轴垂直平分对应点连线，所以$\triangle ABB'$是等腰三角形，$AC$是底边$BB'$上的高，也是顶角$\angle BAB'$的角平分线），又因为$\angle BAC = 30^{\circ}$，所以$\angle BAB'=60^{\circ}$，$\triangle ABB'$是等边三角形（有一个角是$60^{\circ}$的等腰三角形是等边三角形）。
【答案】：$\frac{1}{2}AB$；$AB'$；$\angle B'$；等边；$60^{\circ}$；$30^{\circ}$

例4 如右图所示,BD是△ABC的角平分线,∠ABD= 36°,∠C= 72°,则图中的等腰三角形有______3个。

答案： 【解析】：因为BD是△ABC的角平分线，∠ABD=36°，所以∠DBC=∠ABD=36°，则∠ABC=∠ABD + ∠DBC=36°+36°=72°。在△ABC中，∠A=180° - ∠ABC - ∠C=180° - 72° - 72°=36°。在△ABD中，∠A=∠ABD=36°，所以AD=BD，△ABD是等腰三角形。在△BCD中，∠BDC=180° - ∠DBC - ∠C=180° - 36° - 72°=72°，则∠BDC=∠C=72°，所以BD=BC，△BCD是等腰三角形。在△ABC中，∠ABC=∠C=72°，所以AB=AC，△ABC是等腰三角形。综上，图中的等腰三角形有3个。
【答案】：3

【针对训练4】 如右图,在△ABC中,AB= AC,点D,E在BC上,连接AD,AE,如果只添加一个条件使∠DAB= ∠EAC,则添加的条件不能为(C)

A.BD= CE
B.AD= AE
C.DA= DE
D.BE= CD

答案： 【解析】：在△ABC中，AB=AC，所以△ABC是等腰三角形，∠B=∠C。
选项A：BD=CE
因为AB=AC，∠B=∠C，BD=CE，所以△ABD≌△ACE（SAS），则∠DAB=∠EAC，该条件成立。
选项B：AD=AE
因为AD=AE，所以∠ADE=∠AED，进而∠ADB=∠AEC（邻补角性质）。又因为AB=AC，∠B=∠C，所以△ABD≌△ACE（AAS），则∠DAB=∠EAC，该条件成立。
选项C：DA=DE
DA=DE只能说明△ADE是等腰三角形，无法直接或间接推出∠DAB=∠EAC，与已知条件AB=AC及∠B=∠C无必然关联，该条件不成立。
选项D：BE=CD
因为BE=CD，所以BE - DE=CD - DE，即BD=CE，后续同选项A，可证△ABD≌△ACE，∠DAB=∠EAC，该条件成立。
综上，添加的条件不能为C。
【答案】：C

例5 如右图所示,在△ABC中,∠A= 90°,DE是BC边的垂直平分线,DE交BC于D,交AB于E,如果CE恰是∠ACB的平分线,试求∠B的度数。

答案： 【解析】：
连接$BE$，
因为$DE$是$BC$的垂直平分线，
所以$BE=CE$，
因此$\angle B = \angle ECB$（等边对等角）。
由于$CE$平分$\angle ACB$，
所以$\angle ACE = \angle ECB$。
又因为$\angle A = 90^\circ$，
所以$\angle B + \angle ACB = 90^\circ$。
设$\angle B = x$，
则$\angle ACB = 2x$，
因此$x + 2x = 90^\circ$，
解得$x = 30^\circ$。
所以$\angle B = 30^\circ$。
【答案】：
$\angle B= 30^\circ$

【针对训练5】 如右图所示,在△ABC中,AB= AC= 7cm,腰AB的垂直平分线交AB于E,交BC于D,若BC= 11cm,则△ADC的周长为(B)

A.17cm
B.18cm
C.19cm
D.无法计算

答案： 【解析】：
因为 $ DE $ 是 $ AB $ 的垂直平分线，所以 $ DA=DB $。
所以$\triangle ADC$的周长为$AC+DC+AD=AC+DC+DB=AC+BC=7+11=18$（cm）。
【答案】：B