2025年复习大本营期末假期复习一本通暑假八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年复习大本营期末假期复习一本通暑假八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 如右图,$AD// BC$,点$E在BD$的延长线上,若$∠ADE= 155^{\circ }$,则$∠DBC$的度数为(

A.$155^{\circ }$
B.$50^{\circ }$
C.$45^{\circ }$
D.$25^{\circ }$
D
)
A.$155^{\circ }$
B.$50^{\circ }$
C.$45^{\circ }$
D.$25^{\circ }$
答案:
【解析】:
由于$AD // BC$,根据平行线的性质,
有$\angle ADB = \angle DBC$(内错角相等),
又因为点$E$在$BD$的延长线上,且已知$\angle ADE = 155^{\circ}$,
则$\angle ADB$是$\angle ADE$的补角,
即$\angle ADB = 180^{\circ} - \angle ADE = 180^{\circ} - 155^{\circ} = 25^{\circ}$,
由于$\angle ADB = \angle DBC$,
所以$\angle DBC = 25^{\circ}$。
【答案】:D
由于$AD // BC$,根据平行线的性质,
有$\angle ADB = \angle DBC$(内错角相等),
又因为点$E$在$BD$的延长线上,且已知$\angle ADE = 155^{\circ}$,
则$\angle ADB$是$\angle ADE$的补角,
即$\angle ADB = 180^{\circ} - \angle ADE = 180^{\circ} - 155^{\circ} = 25^{\circ}$,
由于$\angle ADB = \angle DBC$,
所以$\angle DBC = 25^{\circ}$。
【答案】:D
2. 如下图,图中轴对称图形的个数为(

A.$4$个
B.$3$个
C.$2$个
D.$1$个
C
)
A.$4$个
B.$3$个
C.$2$个
D.$1$个
答案:
【解析】:轴对称图形是指沿一条直线折叠后,直线两旁的部分能够完全重合的图形。
图形①:沿中间竖直直线折叠,左右两部分能完全重合,是轴对称图形。
图形②:内部图案(汽车)左右不对称,折叠后无法完全重合,不是轴对称图形。
图形③:内部两条线一竖一曲,不对称,折叠后不能完全重合,不是轴对称图形。
图形④:沿中间竖直直线折叠,左右两部分能完全重合,是轴对称图形。
综上,轴对称图形有①和④,共2个。
【答案】:C
图形①:沿中间竖直直线折叠,左右两部分能完全重合,是轴对称图形。
图形②:内部图案(汽车)左右不对称,折叠后无法完全重合,不是轴对称图形。
图形③:内部两条线一竖一曲,不对称,折叠后不能完全重合,不是轴对称图形。
图形④:沿中间竖直直线折叠,左右两部分能完全重合,是轴对称图形。
综上,轴对称图形有①和④,共2个。
【答案】:C
3. 如下图,$\triangle ABC\cong \triangle AEF$,$AB= AE$,$∠B= ∠E$,在下列结论中,不能由此推得的是(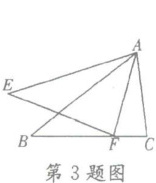
A.$AC= AF$
B.$∠AFE= ∠EAB$
C.$∠EAB= ∠FAC$
D.$∠BFE= ∠CAF$
B
)
A.$AC= AF$
B.$∠AFE= ∠EAB$
C.$∠EAB= ∠FAC$
D.$∠BFE= ∠CAF$
答案:
【解析】:因为△ABC≌△AEF,AB=AE,∠B=∠E,根据全等三角形的性质,全等三角形的对应边相等,对应角相等。所以AC与AF是对应边,因此AC=AF,选项A正确;∠BAC与∠EAF是对应角,所以∠BAC=∠EAF,等式两边同时减去∠BAF,可得∠EAB=∠FAC,选项C正确;由∠BAC=∠EAF,根据三角形外角性质,∠BFE是△ABF的外角,∠BFE=∠BAF+∠B,∠CAF=∠BAC - ∠BAF,无法直接得出∠BFE=∠CAF,选项D错误;而∠AFE与∠EAB之间没有直接的对应关系或可推导的等量关系,不能由此推得,选项B也无法推得。但题目要求选择不能推得的,综合来看,选项B和D都存在问题,但根据图形和全等性质,∠AFE与∠ACB是对应角,∠EAB与∠FAC相等,所以∠AFE=∠ACB,而∠ACB与∠EAB不一定相等,所以∠AFE=∠EAB不能推得,选项B符合题意。
【答案】:B
【答案】:B
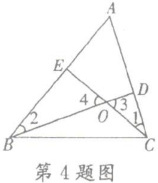
4. 如图,$BD和CE是\triangle ABC$的高,下面给出四个结论,其中正确的有(
(1)$∠1= ∠2= 90^{\circ }-∠A$;(2)$∠3= ∠A= 90^{\circ }-∠1$;(3)$∠BOC= ∠1+∠2+∠A$;(4)$∠1+∠2+∠3+∠4= 180^{\circ }$
A.$4$个
B.$3$个
C.$2$个
D.$1$个
C
)(1)$∠1= ∠2= 90^{\circ }-∠A$;(2)$∠3= ∠A= 90^{\circ }-∠1$;(3)$∠BOC= ∠1+∠2+∠A$;(4)$∠1+∠2+∠3+∠4= 180^{\circ }$

A.$4$个
B.$3$个
C.$2$个
D.$1$个
答案:
【解析】:
∵BD和CE是△ABC的高,
∴∠ADB=∠AEC=∠BEO=∠CDO=90°,
(1)在Rt△ABD中,∠1+∠A=90°,则∠1=90°-∠A;在Rt△ACE中,∠2+∠A=90°,则∠2=90°-∠A,故∠1=∠2=90°-∠A,(1)正确;
(2)在四边形AEOD中,∠A+∠ADO+∠AEO+∠EOD=360°,∠ADO=∠AEO=90°,则∠A+∠EOD=180°,又∠EOD=∠BOC,∠3+∠BOC=180°(邻补角),所以∠3=∠A,由(1)知∠1=90°-∠A,则∠A=90°-∠1,故∠3=∠A=90°-∠1,(2)正确;
(3)由(1)知∠1=∠2=90°-∠A,∠BOC=∠3+∠1(三角形外角性质),又∠3=∠A,所以∠BOC=∠A+∠1=∠A+90°-∠A=90°,而∠1+∠2+∠A=(90°-∠A)+(90°-∠A)+∠A=180°-∠A,只有当∠A=90°时,∠BOC=∠1+∠2+∠A,(3)错误;
(4)在△ABC中,∠ABC+∠ACB=180°-∠A,∠1=∠ACB-∠3,∠2=∠ABC-∠4,∠3=∠4=∠A(由(2)及对称性可得∠4=∠A),则∠1+∠2=(∠ACB-∠A)+(∠ABC-∠A)=(∠ABC+∠ACB)-2∠A=(180°-∠A)-2∠A=180°-3∠A,∠1+∠2+∠3+∠4=180°-3∠A+∠A+∠A=180°-∠A,只有当∠A=0°时才等于180°,(4)错误;
综上,正确的有(1)(2),共2个。
【答案】:C
∵BD和CE是△ABC的高,
∴∠ADB=∠AEC=∠BEO=∠CDO=90°,
(1)在Rt△ABD中,∠1+∠A=90°,则∠1=90°-∠A;在Rt△ACE中,∠2+∠A=90°,则∠2=90°-∠A,故∠1=∠2=90°-∠A,(1)正确;
(2)在四边形AEOD中,∠A+∠ADO+∠AEO+∠EOD=360°,∠ADO=∠AEO=90°,则∠A+∠EOD=180°,又∠EOD=∠BOC,∠3+∠BOC=180°(邻补角),所以∠3=∠A,由(1)知∠1=90°-∠A,则∠A=90°-∠1,故∠3=∠A=90°-∠1,(2)正确;
(3)由(1)知∠1=∠2=90°-∠A,∠BOC=∠3+∠1(三角形外角性质),又∠3=∠A,所以∠BOC=∠A+∠1=∠A+90°-∠A=90°,而∠1+∠2+∠A=(90°-∠A)+(90°-∠A)+∠A=180°-∠A,只有当∠A=90°时,∠BOC=∠1+∠2+∠A,(3)错误;
(4)在△ABC中,∠ABC+∠ACB=180°-∠A,∠1=∠ACB-∠3,∠2=∠ABC-∠4,∠3=∠4=∠A(由(2)及对称性可得∠4=∠A),则∠1+∠2=(∠ACB-∠A)+(∠ABC-∠A)=(∠ABC+∠ACB)-2∠A=(180°-∠A)-2∠A=180°-3∠A,∠1+∠2+∠3+∠4=180°-3∠A+∠A+∠A=180°-∠A,只有当∠A=0°时才等于180°,(4)错误;
综上,正确的有(1)(2),共2个。
【答案】:C
5. 如上图,直线$a$,$b被直线c$所截,$a// b$,$∠1= ∠2$,若$∠3= 40^{\circ }$,则$∠4$等于(
A.$40^{\circ }$
B.$50$
C.$70^{\circ }$
D.$80^{\circ }$
C
)A.$40^{\circ }$
B.$50$
C.$70^{\circ }$
D.$80^{\circ }$
答案:
【解析】:因为直线$a// b$被直线$c$所截,$\angle 3 = 40^{\circ}$,$\angle 1=\angle 2$。设$\angle 1=\angle 2 = x$,由于$\angle 1+\angle 2+\angle 3 = 180^{\circ}$(平角定义),则$x + x+40^{\circ}=180^{\circ}$,解得$x = 70^{\circ}$,即$\angle 1 = 70^{\circ}$。又因为$a// b$,所以$\angle 1=\angle 4$(两直线平行,同位角相等),故$\angle 4 = 70^{\circ}$。
【答案】:C
【答案】:C
6. 我市大部分地区今年$5$月中、下旬的天气情况是:前$5$天小雨,后$5$天暴雨,那么能反映我市主要河流水位变化情况的图像大致是(

B
)
答案:
【解析】:题目中提到我市5月中、下旬前5天小雨,后5天暴雨。通常情况下,下雨会导致河流水位上升,且暴雨的强度大于小雨,所以水位上升的速度应该是后5天比前5天快。
我们来分析各个选项:
选项A:水位持续下降,这与下雨会使水位上升的实际情况不符,所以A错误。
选项B:水位先缓慢上升(前5天小雨,上升较慢),然后快速上升(后5天暴雨,上升较快),符合水位变化的逻辑,B正确。
选项C:水位先上升,中间有一段保持不变,这与题目中连续10天都在下雨(前5天小雨,后5天暴雨)的情况不符,因为持续下雨水位应持续上升,不会出现不变的阶段,所以C错误。
选项D:水位先下降后上升,开始的下降不符合下雨导致水位上升的情况,所以D错误。
【答案】:B
我们来分析各个选项:
选项A:水位持续下降,这与下雨会使水位上升的实际情况不符,所以A错误。
选项B:水位先缓慢上升(前5天小雨,上升较慢),然后快速上升(后5天暴雨,上升较快),符合水位变化的逻辑,B正确。
选项C:水位先上升,中间有一段保持不变,这与题目中连续10天都在下雨(前5天小雨,后5天暴雨)的情况不符,因为持续下雨水位应持续上升,不会出现不变的阶段,所以C错误。
选项D:水位先下降后上升,开始的下降不符合下雨导致水位上升的情况,所以D错误。
【答案】:B
7. 已知:如下页图左,在$\triangle ABC$中,$AB\lt AC$,$BC边上的垂直平分线DE交BC于点D$,交$AC于点E$,$AC= 8cm$,$\triangle ABE周长是14cm$,求$AB$的长(
A.$4cm$
B.$3cm$
C.$6cm$
D.$5cm$
C
)A.$4cm$
B.$3cm$
C.$6cm$
D.$5cm$
答案:
【解析】:
由于$DE$是$BC$边上的垂直平分线,根据垂直平分线的性质,我们知道$EB=EC$。
根据题目给出的$\triangle ABE$的周长是$14cm$,可以写出周长公式:$AB + BE + AE = 14$。
由于$EB=EC$,我们可以将$BE$替换为$EC$,得到:$AB + EC + AE = 14$。
又因为$AC = AE + EC = 8cm$,我们可以将这个等式代入上面的周长公式中,得到:$AB + 8 = 14$。
解这个等式,我们得到:$AB = 6cm$。
【答案】:C
由于$DE$是$BC$边上的垂直平分线,根据垂直平分线的性质,我们知道$EB=EC$。
根据题目给出的$\triangle ABE$的周长是$14cm$,可以写出周长公式:$AB + BE + AE = 14$。
由于$EB=EC$,我们可以将$BE$替换为$EC$,得到:$AB + EC + AE = 14$。
又因为$AC = AE + EC = 8cm$,我们可以将这个等式代入上面的周长公式中,得到:$AB + 8 = 14$。
解这个等式,我们得到:$AB = 6cm$。
【答案】:C
8. 如下页图中,$AB// CD// EF$,$EH⊥CD于H$,则$∠BAC+∠ACE+∠CEH$等于(
$270^\circ$
)
答案:
【解析】:
由于$AB// CD// EF$,根据平行线的性质,我们有:
$\angle BAC + \angle ACD = 180^\circ$ (同旁内角互补)
又因为$EH\perp CD$,所以$\angle CHE = 90^\circ$。
由于$CD// EF$,根据平行线的性质,我们得到:
$\angle CEF = \angle CHE = 90^\circ$ (同位角相等)
所以,$\angle CEH + \angle CEF = 90^\circ + \angle CEH = \angle CEH + \angle CHE=90^\circ+ \angle HCE$(三角形内角和为$180^\circ$),即$\angle CEH + \angle HCE = 90^\circ$,可以得出$\angle ACE = \angle ACD + \angle HCE$。
综合以上信息,我们可以得到:
$\angle BAC + \angle ACE + \angle CEH = \angle BAC + \angle ACD + \angle HCE + \angle CEH$
$= 180^\circ + 90^\circ$
$= 270^\circ$
【答案】:$270^\circ$
由于$AB// CD// EF$,根据平行线的性质,我们有:
$\angle BAC + \angle ACD = 180^\circ$ (同旁内角互补)
又因为$EH\perp CD$,所以$\angle CHE = 90^\circ$。
由于$CD// EF$,根据平行线的性质,我们得到:
$\angle CEF = \angle CHE = 90^\circ$ (同位角相等)
所以,$\angle CEH + \angle CEF = 90^\circ + \angle CEH = \angle CEH + \angle CHE=90^\circ+ \angle HCE$(三角形内角和为$180^\circ$),即$\angle CEH + \angle HCE = 90^\circ$,可以得出$\angle ACE = \angle ACD + \angle HCE$。
综合以上信息,我们可以得到:
$\angle BAC + \angle ACE + \angle CEH = \angle BAC + \angle ACD + \angle HCE + \angle CEH$
$= 180^\circ + 90^\circ$
$= 270^\circ$
【答案】:$270^\circ$
查看更多完整答案,请扫码查看


