2025年复习大本营期末假期复习一本通暑假八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年复习大本营期末假期复习一本通暑假八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
23. 如图,在$\triangle ABC$中,$∠C= 2∠B$,$AD是\triangle ABC$的角平分线,$∠1= ∠B$。
求证:$AB= AC+CD$。
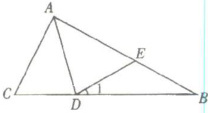
求证:$AB= AC+CD$。

答案:
【解析】:
在$AB$上截取$AE=AC$,连接$DE$。
因为$AD$是$\triangle ABC$的角平分线,所以$\angle CAD=\angle EAD$。
在$\triangle ACD$和$\triangle AED$中:
$\begin{cases}AC = AE,\\\angle CAD=\angle EAD,\\AD = AD.\end{cases}$
根据全等三角形判定定理(SAS:两边及其夹角对应相等的三角形全等),可得$\triangle ACD\cong\triangle AED$。
由全等三角形的性质可知$CD = DE$,$\angle C=\angle AED$。
已知$\angle C = 2\angle B$,$\angle 1=\angle B$,且$\angle AED=\angle 1+\angle EDB$,所以$\angle AED=\angle B+\angle EDB = 2\angle B$,则$\angle EDB=\angle B$。
根据等角对等边,可得$EB = ED$。
因为$CD = DE$,$EB = ED$,所以$EB = CD$。
又因为$AB=AE + EB$,$AC = AE$,所以$AB=AC + CD$。
【答案】:
在$AB$上截取$AE = AC$,连接$DE$,通过证明$\triangle ACD\cong\triangle AED$,得出$CD = DE$,再结合已知条件推出$EB = CD$,进而证明$AB=AC + CD$。
在$AB$上截取$AE=AC$,连接$DE$。
因为$AD$是$\triangle ABC$的角平分线,所以$\angle CAD=\angle EAD$。
在$\triangle ACD$和$\triangle AED$中:
$\begin{cases}AC = AE,\\\angle CAD=\angle EAD,\\AD = AD.\end{cases}$
根据全等三角形判定定理(SAS:两边及其夹角对应相等的三角形全等),可得$\triangle ACD\cong\triangle AED$。
由全等三角形的性质可知$CD = DE$,$\angle C=\angle AED$。
已知$\angle C = 2\angle B$,$\angle 1=\angle B$,且$\angle AED=\angle 1+\angle EDB$,所以$\angle AED=\angle B+\angle EDB = 2\angle B$,则$\angle EDB=\angle B$。
根据等角对等边,可得$EB = ED$。
因为$CD = DE$,$EB = ED$,所以$EB = CD$。
又因为$AB=AE + EB$,$AC = AE$,所以$AB=AC + CD$。
【答案】:
在$AB$上截取$AE = AC$,连接$DE$,通过证明$\triangle ACD\cong\triangle AED$,得出$CD = DE$,再结合已知条件推出$EB = CD$,进而证明$AB=AC + CD$。
24. 如图,在等边$\triangle ABC$中,$∠ABC和∠ACB的平分线相交于点O$,$BO$,$OC的垂直平分线分别交BC于点E$,$F$,求证:$\triangle OEF$是等边三角形。


答案:
【解析】:
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°。
∵BO、CO分别平分∠ABC和∠ACB,
∴∠OBC=∠OCB=30°。
∵EG是BO的垂直平分线(设G为BO中点),
∴EB=EO(垂直平分线上的点到线段两端距离相等),
∴∠EOB=∠OBC=30°,
∴∠OEF=∠EOB+∠OBC=30°+30°=60°。
同理,FH是CO的垂直平分线(设H为CO中点),
∴FC=FO,
∴∠FOC=∠OCB=30°,
∴∠OFE=∠FOC+∠OCB=30°+30°=60°。
在△OEF中,∠OEF=∠OFE=60°,
∴∠EOF=180°-60°-60°=60°,
∴△OEF是等边三角形。
【答案】:△OEF是等边三角形。
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°。
∵BO、CO分别平分∠ABC和∠ACB,
∴∠OBC=∠OCB=30°。
∵EG是BO的垂直平分线(设G为BO中点),
∴EB=EO(垂直平分线上的点到线段两端距离相等),
∴∠EOB=∠OBC=30°,
∴∠OEF=∠EOB+∠OBC=30°+30°=60°。
同理,FH是CO的垂直平分线(设H为CO中点),
∴FC=FO,
∴∠FOC=∠OCB=30°,
∴∠OFE=∠FOC+∠OCB=30°+30°=60°。
在△OEF中,∠OEF=∠OFE=60°,
∴∠EOF=180°-60°-60°=60°,
∴△OEF是等边三角形。
【答案】:△OEF是等边三角形。
25. 如图,在$\triangle ABC$中,$∠ACB= 90^{\circ }$,$AC= BC$,延长$AB至点D$,使$DB= AB$,连接$CD$,以$CD为直角边作等腰直角三角形CDE$,其中$∠DCE= 90^{\circ }$,连接$BE$。
求证:$\triangle ACD\cong \triangle BCE$。
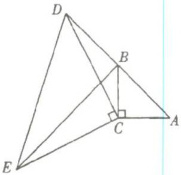
求证:$\triangle ACD\cong \triangle BCE$。

答案:
【解析】:
∵在$\triangle ABC$中,$\angle ACB = 90^\circ$,$AC = BC$,
∴$\triangle ABC$是等腰直角三角形,$\angle ABC = \angle BAC = 45^\circ$,$AB = \sqrt{2}AC$(此处可省略长度关系,仅需角度)。
∵$DB = AB$,
∴点$B$为$AD$的中点(或$AD = 2AB$,但无需长度)。
∵$\triangle CDE$是等腰直角三角形,$\angle DCE = 90^\circ$,
∴$CD = CE$,$\angle DCE = 90^\circ$。
∵$\angle ACB = 90^\circ$,$\angle DCE = 90^\circ$,
∴$\angle ACB + \angle BCD = \angle DCE + \angle BCD$(等式性质),
即$\angle ACD = \angle BCE$。
在$\triangle ACD$和$\triangle BCE$中:
$\begin{cases} AC = BC & (\text{已知}) \\\angle ACD = \angle BCE & (\text{已证}) \\CD = CE & (\text{等腰直角三角形性质}) \end{cases}$
∴$\triangle ACD \cong \triangle BCE$(SAS)。
【答案】:$\triangle ACD\cong \triangle BCE$
∵在$\triangle ABC$中,$\angle ACB = 90^\circ$,$AC = BC$,
∴$\triangle ABC$是等腰直角三角形,$\angle ABC = \angle BAC = 45^\circ$,$AB = \sqrt{2}AC$(此处可省略长度关系,仅需角度)。
∵$DB = AB$,
∴点$B$为$AD$的中点(或$AD = 2AB$,但无需长度)。
∵$\triangle CDE$是等腰直角三角形,$\angle DCE = 90^\circ$,
∴$CD = CE$,$\angle DCE = 90^\circ$。
∵$\angle ACB = 90^\circ$,$\angle DCE = 90^\circ$,
∴$\angle ACB + \angle BCD = \angle DCE + \angle BCD$(等式性质),
即$\angle ACD = \angle BCE$。
在$\triangle ACD$和$\triangle BCE$中:
$\begin{cases} AC = BC & (\text{已知}) \\\angle ACD = \angle BCE & (\text{已证}) \\CD = CE & (\text{等腰直角三角形性质}) \end{cases}$
∴$\triangle ACD \cong \triangle BCE$(SAS)。
【答案】:$\triangle ACD\cong \triangle BCE$
查看更多完整答案,请扫码查看


