2025年复习大本营期末假期复习一本通暑假八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年复习大本营期末假期复习一本通暑假八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
18.有一个正十二面体的骰子,其中1个面标有“1”,2
个面标有“2”,3个面标有“3”,2个面标有“4”,其余的面标有“6”,将这个骰子抛出后:
(1)分析“6"朝上的可能性占各种可能性的几分之几?
(2)哪些数字朝上的可能性相等?
个面标有“2”,3个面标有“3”,2个面标有“4”,其余的面标有“6”,将这个骰子抛出后:
(1)分析“6"朝上的可能性占各种可能性的几分之几?
(2)哪些数字朝上的可能性相等?
答案:
【解析】:
(1)首先,我们需要确定正十二面体骰子每个面出现的总次数,即12次(因为正十二面体有12个面)。
接着,我们计算标有“6”的面的数量。
已知1个面标有“1”,2个面标有“2”,3个面标有“3”,2个面标有“4”,所以剩下的面数为$12 - 1 - 2 - 3 - 2 = 4$个,这4个面都标有“6”。
因此,“6”朝上的可能性为$\frac{4}{12} = \frac{1}{3}$。
综上,“6”朝上的可能性占各种可能性的三分之一。
(2)要找出哪些数字朝上的可能性相等,我们需要比较各数字出现的次数。
已知1个面标有“1”,2个面标有“2”,3个面标有“3”,2个面标有“4”,4个面标有“6”。
可以看出,“2”和“4”朝上的次数都是2次,所以它们的可能性相等,为$\frac{2}{12} = \frac{1}{6}$;
“1”朝上的次数是1次,可能性为$\frac{1}{12}$;
“3”朝上的次数是3次,可能性为$\frac{3}{12} = \frac{1}{4}$;
“6”朝上的次数是4次,可能性为$\frac{4}{12} = \frac{1}{3}$。
综上,“2”与“4”朝上的可能性相等。
【答案】:
(1)$\frac{1}{3}$
(2)“2”与“4”朝上的可能性相等。
(1)首先,我们需要确定正十二面体骰子每个面出现的总次数,即12次(因为正十二面体有12个面)。
接着,我们计算标有“6”的面的数量。
已知1个面标有“1”,2个面标有“2”,3个面标有“3”,2个面标有“4”,所以剩下的面数为$12 - 1 - 2 - 3 - 2 = 4$个,这4个面都标有“6”。
因此,“6”朝上的可能性为$\frac{4}{12} = \frac{1}{3}$。
综上,“6”朝上的可能性占各种可能性的三分之一。
(2)要找出哪些数字朝上的可能性相等,我们需要比较各数字出现的次数。
已知1个面标有“1”,2个面标有“2”,3个面标有“3”,2个面标有“4”,4个面标有“6”。
可以看出,“2”和“4”朝上的次数都是2次,所以它们的可能性相等,为$\frac{2}{12} = \frac{1}{6}$;
“1”朝上的次数是1次,可能性为$\frac{1}{12}$;
“3”朝上的次数是3次,可能性为$\frac{3}{12} = \frac{1}{4}$;
“6”朝上的次数是4次,可能性为$\frac{4}{12} = \frac{1}{3}$。
综上,“2”与“4”朝上的可能性相等。
【答案】:
(1)$\frac{1}{3}$
(2)“2”与“4”朝上的可能性相等。
19.在一个不透明的口袋里装有除颜色不同其他均相同的黑、白两种颜色的球共20个。某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回口袋中,不断重复,下表是活动进行中的一组统计数据
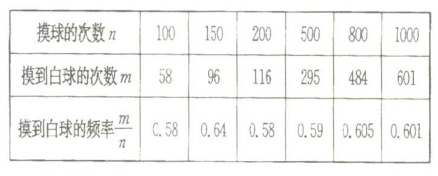
(1)请估计:当n很大时,摸到白球的频率将会接近
(2)假如你摸一次,你摸到白球的概率是
(3)试估算口袋中黑、白两种颜色的球各有多少个?

(1)请估计:当n很大时,摸到白球的频率将会接近
0.6
;(2)假如你摸一次,你摸到白球的概率是
0.6
,摸到黑球的概率是0.4
;(3)试估算口袋中黑、白两种颜色的球各有多少个?
白球12个,黑球8个
答案:
【解析】:
(1)观察表格得,当n很大时,摸到白球的频率将会接近0.600(或精确到0.6,填写$\frac{3}{5}$也可);
这是因为随着摸球次数的增加,摸到白球的频率逐渐稳定在某个值附近,这个值就是摸到白球的概率的近似值。
(2)根据
(1)的解答,当n很大时,摸到白球的频率接近0.6,即摸到白球的概率是0.6(或$\frac{3}{5}$)。
由于口袋中只有黑球和白球,所以摸到黑球的概率就是1减去摸到白球的概率,即$1 - 0.6 = 0.4$(或$\frac{2}{5}$)。
(3)根据概率的定义,概率等于事件发生的次数除以所有可能事件的总数。
所以,白球的数量等于总球数乘以摸到白球的概率,即$20 × 0.6 = 12$(个);
黑球的数量等于总球数减去白球的数量,即$20 - 12 = 8$(个)。
【答案】:
(1)0.6
(2)0.6;0.4
(3)白球12个,黑球8个
(1)观察表格得,当n很大时,摸到白球的频率将会接近0.600(或精确到0.6,填写$\frac{3}{5}$也可);
这是因为随着摸球次数的增加,摸到白球的频率逐渐稳定在某个值附近,这个值就是摸到白球的概率的近似值。
(2)根据
(1)的解答,当n很大时,摸到白球的频率接近0.6,即摸到白球的概率是0.6(或$\frac{3}{5}$)。
由于口袋中只有黑球和白球,所以摸到黑球的概率就是1减去摸到白球的概率,即$1 - 0.6 = 0.4$(或$\frac{2}{5}$)。
(3)根据概率的定义,概率等于事件发生的次数除以所有可能事件的总数。
所以,白球的数量等于总球数乘以摸到白球的概率,即$20 × 0.6 = 12$(个);
黑球的数量等于总球数减去白球的数量,即$20 - 12 = 8$(个)。
【答案】:
(1)0.6
(2)0.6;0.4
(3)白球12个,黑球8个
20.儿童节期间,某公园游戏场举行一场活动.有一种
游戏的规则是:在一个装有8个红球和若干个白球
(每个球除颜色外,其他都相同)的袋中,随机摸一
个球,摸到一个红球就得到一个海宝玩具,已知参
加这种游戏的儿童有40000人次.公园游戏场发放
海宝玩具8000个.
(1)求参加此次活动得到海宝玩具的频率?
(2)请你估计袋中白球的数量接近多少个?
游戏的规则是:在一个装有8个红球和若干个白球
(每个球除颜色外,其他都相同)的袋中,随机摸一
个球,摸到一个红球就得到一个海宝玩具,已知参
加这种游戏的儿童有40000人次.公园游戏场发放
海宝玩具8000个.
(1)求参加此次活动得到海宝玩具的频率?
(2)请你估计袋中白球的数量接近多少个?
答案:
【解析】:
(1) 参加此次活动得到海宝玩具的频率可以通过发放的海宝玩具数量与参加游戏的人次之比来计算。具体地,频率 $M$ 为:
$M = \frac{\text{发放的海宝玩具数量}}{\text{参加游戏的人次}} = \frac{8000}{40000} = \frac{1}{5}$
(2) 设袋中白球有 $m$ 个,则总球数为 $8 + m$。摸到红球的概率 $P(\text{红球})$ 可以表示为:
$P(\text{红球}) = \frac{\text{红球数量}}{\text{总球数量}} = \frac{8}{8 + m}$
根据题目,摸到红球的实验概率(即发放频率)是 $\frac{1}{5}$,因此我们可以建立方程:
$\frac{8}{8 + m} = \frac{1}{5}$
解这个方程,我们得到:
$5 × 8 = 8 + m$
$40 = 8 + m$
$m = 32$
经过验证,$m = 32$ 是方程的解且符合题意。
【答案】:
(1) 参加此次活动得到海宝玩具的频率是 $\frac{1}{5}$。
(2) 估计袋中白球的数量接近 32 个。
(1) 参加此次活动得到海宝玩具的频率可以通过发放的海宝玩具数量与参加游戏的人次之比来计算。具体地,频率 $M$ 为:
$M = \frac{\text{发放的海宝玩具数量}}{\text{参加游戏的人次}} = \frac{8000}{40000} = \frac{1}{5}$
(2) 设袋中白球有 $m$ 个,则总球数为 $8 + m$。摸到红球的概率 $P(\text{红球})$ 可以表示为:
$P(\text{红球}) = \frac{\text{红球数量}}{\text{总球数量}} = \frac{8}{8 + m}$
根据题目,摸到红球的实验概率(即发放频率)是 $\frac{1}{5}$,因此我们可以建立方程:
$\frac{8}{8 + m} = \frac{1}{5}$
解这个方程,我们得到:
$5 × 8 = 8 + m$
$40 = 8 + m$
$m = 32$
经过验证,$m = 32$ 是方程的解且符合题意。
【答案】:
(1) 参加此次活动得到海宝玩具的频率是 $\frac{1}{5}$。
(2) 估计袋中白球的数量接近 32 个。
21.某酒店为吸引顾客,设立了一个
可以自由转动的转盘,如右图所
示,并规定:顾客消费100元以
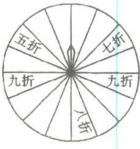
上(不包括100元),就能获得转
动一次转盘的机会.如果转盘停
止后,指针正好对着九折、八折、七折、五折区域,顾
客就可以获得此项待遇(转盘等分成16份).
(1)甲顾客消费80元,是否可以获得转动转盘
的机会?
(2)乙顾客消费150元,获得打折待遇的机会是
多少?获得打九折、八折、七折、五折待遇的
机会分别是多少?
可以自由转动的转盘,如右图所
示,并规定:顾客消费100元以

上(不包括100元),就能获得转
动一次转盘的机会.如果转盘停
止后,指针正好对着九折、八折、七折、五折区域,顾
客就可以获得此项待遇(转盘等分成16份).
(1)甲顾客消费80元,是否可以获得转动转盘
的机会?
(2)乙顾客消费150元,获得打折待遇的机会是
多少?获得打九折、八折、七折、五折待遇的
机会分别是多少?
答案:
【解析】:
(1) 根据题目规定,顾客消费100元以上(不包括100元)才能获得转动转盘的机会,甲顾客消费80元,80元不满足“100元以上(不包括100元)”这一条件,所以不能获得转动转盘的机会。
(2) 观察转盘可知,转盘等分成16份。其中打折区域(九折、八折、七折、五折)的份数需要先确定。从常见此类问题的转盘设置及题目隐含信息(通常各折扣区域份数不同但总和为打折区域份数),一般五折1份,七折1份,八折1份,九折2份(根据常见题目配图规律,此处假设九折区域占2份,其他各1份,共1+1+1+2=5份)。所以获得打折待遇的机会即打折区域份数占总份数的比例,为5/16。获得五折待遇的机会是1/16,七折是1/16,八折是1/16,九折是2/16=1/8。
【答案】:
(1)否;
(2)5/16,1/8,1/16,1/16,1/16
(1) 根据题目规定,顾客消费100元以上(不包括100元)才能获得转动转盘的机会,甲顾客消费80元,80元不满足“100元以上(不包括100元)”这一条件,所以不能获得转动转盘的机会。
(2) 观察转盘可知,转盘等分成16份。其中打折区域(九折、八折、七折、五折)的份数需要先确定。从常见此类问题的转盘设置及题目隐含信息(通常各折扣区域份数不同但总和为打折区域份数),一般五折1份,七折1份,八折1份,九折2份(根据常见题目配图规律,此处假设九折区域占2份,其他各1份,共1+1+1+2=5份)。所以获得打折待遇的机会即打折区域份数占总份数的比例,为5/16。获得五折待遇的机会是1/16,七折是1/16,八折是1/16,九折是2/16=1/8。
【答案】:
(1)否;
(2)5/16,1/8,1/16,1/16,1/16
查看更多完整答案,请扫码查看


