2025年复习大本营期末假期复习一本通暑假八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年复习大本营期末假期复习一本通暑假八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
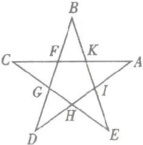
25. 如下图所示,有一个五角星 $ABCDE$,你能求出$\angle A + \angle B + \angle C + \angle D + \angle E$ 的度数吗?

答案:
【解析】:在五角星ABCDE中,连接CD。在△BGD中,∠BGD是其一个外角,根据三角形外角性质可得∠BGD=∠B+∠E。又因为∠BGD与∠CGD是对顶角,所以∠CGD=∠B+∠E。在△CGD和△ACD中,∠A+∠C+∠D+∠CGD=180°(三角形内角和为180°),将∠CGD=∠B+∠E代入可得∠A+∠B+∠C+∠D+∠E=180°。
【答案】:180°
【答案】:180°
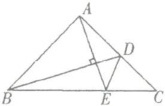
26. 已知:如下图所示,$\triangle ABC$ 中,$\angle BAC = 90^{\circ}$,$AB = AC$,$D$ 为 $AC$ 中点,$AE \perp BD$,交 $BC$ 于 $E$,试说明$\angle ADB = \angle CDE$.

答案:
【解析】:过点 $ C $ 作 $ CG \perp AC $ 交 $ AE $ 的延长线于点 $ G $。
因为 $ \angle BAC = 90^{\circ} $,$ AE \perp BD $,所以 $ \angle ABD + \angle ADB = 90^{\circ} $,$ \angle CAG + \angle ADB = 90^{\circ} $,故 $ \angle ABD = \angle CAG $。
在 $ \triangle ABD $ 和 $ \triangle CAG $ 中,$ \angle BAD = \angle ACG = 90^{\circ} $,$ AB = AC $,$ \angle ABD = \angle CAG $,所以 $ \triangle ABD \cong \triangle CAG $(ASA),因此 $ AD = CG $,$ \angle ADB = \angle G $。
因为 $ D $ 为 $ AC $ 中点,所以 $ AD = CD $,则 $ CD = CG $。
由于 $ AB = AC $,$ \angle BAC = 90^{\circ} $,所以 $ \angle ACB = 45^{\circ} $,又因为 $ CG \perp AC $,所以 $ \angle GCE = 45^{\circ} = \angle DCE $。
在 $ \triangle CDE $ 和 $ \triangle CGE $ 中,$ CD = CG $,$ \angle DCE = \angle GCE $,$ CE = CE $,所以 $ \triangle CDE \cong \triangle CGE $(SAS),故 $ \angle CDE = \angle G $。
综上,$ \angle ADB = \angle CDE $。
【答案】:$\angle ADB = \angle CDE$
因为 $ \angle BAC = 90^{\circ} $,$ AE \perp BD $,所以 $ \angle ABD + \angle ADB = 90^{\circ} $,$ \angle CAG + \angle ADB = 90^{\circ} $,故 $ \angle ABD = \angle CAG $。
在 $ \triangle ABD $ 和 $ \triangle CAG $ 中,$ \angle BAD = \angle ACG = 90^{\circ} $,$ AB = AC $,$ \angle ABD = \angle CAG $,所以 $ \triangle ABD \cong \triangle CAG $(ASA),因此 $ AD = CG $,$ \angle ADB = \angle G $。
因为 $ D $ 为 $ AC $ 中点,所以 $ AD = CD $,则 $ CD = CG $。
由于 $ AB = AC $,$ \angle BAC = 90^{\circ} $,所以 $ \angle ACB = 45^{\circ} $,又因为 $ CG \perp AC $,所以 $ \angle GCE = 45^{\circ} = \angle DCE $。
在 $ \triangle CDE $ 和 $ \triangle CGE $ 中,$ CD = CG $,$ \angle DCE = \angle GCE $,$ CE = CE $,所以 $ \triangle CDE \cong \triangle CGE $(SAS),故 $ \angle CDE = \angle G $。
综上,$ \angle ADB = \angle CDE $。
【答案】:$\angle ADB = \angle CDE$
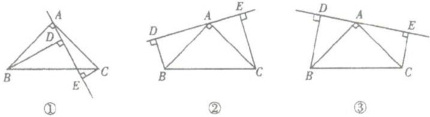
如下图 20① 所示,在$\triangle ABC$ 中,$\angle BAC = 90^{\circ}$,$AB = AC$,$AE$ 是过点 $A$ 的一条直线,且 $B$,$C$ 在 $AE$ 的异侧,$BD \perp AE$ 于 $D$,$CE \perp AE$ 于 $E$.
(1) 试说明:$BD = DE + CE$.
(2) 若直线 $AE$ 绕 $A$ 点旋转到如图② 所示的位置 ($BD < CE$ 时),其余条件不变,则 $BD$ 与 $DE$,$CE$ 的关系如何?请予以说明.
(3) 若直线 $AE$ 绕 $A$ 点旋转到如图③ 所示的位置 ($BD > CE$ 时),其余条件不变,则 $BD$ 与 $DE$,$CE$ 的关系如何?请直接写出结果,不需说明.
(4) 归纳上述(1)(2)(3) 问,请用简洁的语言表达 $BD$,$DE$,$CE$ 的关系.
(1) 试说明:$BD = DE + CE$.
(2) 若直线 $AE$ 绕 $A$ 点旋转到如图② 所示的位置 ($BD < CE$ 时),其余条件不变,则 $BD$ 与 $DE$,$CE$ 的关系如何?请予以说明.
(3) 若直线 $AE$ 绕 $A$ 点旋转到如图③ 所示的位置 ($BD > CE$ 时),其余条件不变,则 $BD$ 与 $DE$,$CE$ 的关系如何?请直接写出结果,不需说明.
(4) 归纳上述(1)(2)(3) 问,请用简洁的语言表达 $BD$,$DE$,$CE$ 的关系.

答案:
【解析】:
(1) 因为 $\angle BAC = 90^{\circ}$,所以 $\angle BAD + \angle CAE = 90^{\circ}$。又因为 $BD \perp AE$,$CE \perp AE$,所以 $\angle ADB = \angle AEC = 90^{\circ}$,$\angle BAD + \angle ABD = 90^{\circ}$,故 $\angle ABD = \angle CAE$。在 $\triangle ABD$ 和 $\triangle CAE$ 中,$\angle ADB = \angle AEC$,$\angle ABD = \angle CAE$,$AB = AC$,所以 $\triangle ABD \cong \triangle CAE(AAS)$,则 $BD = AE$,$AD = CE$。因为 $AE = AD + DE = CE + DE$,所以 $BD = DE + CE$。
(2) 同理,$\angle BAC = 90^{\circ}$ 得 $\angle BAD + \angle CAE = 90^{\circ}$,$BD \perp AE$ 得 $\angle BAD + \angle ABD = 90^{\circ}$,所以 $\angle ABD = \angle CAE$。$\triangle ABD \cong \triangle CAE(AAS)$,$BD = AE$,$AD = CE$。此时 $AE = DE - AD = DE - CE$,所以 $BD = DE - CE$。
(3) 由旋转性质及全等三角形可得 $BD = CE - DE$。
(4) 综合三种情况,当 $B$,$C$ 在 $AE$ 异侧且 $D$,$E$ 在 $A$ 两侧时 $BD = DE + CE$;同侧时,若 $BD < CE$ 则 $BD = DE - CE$,若 $BD > CE$ 则 $BD = CE - DE$,统一为 $BD = |DE - CE|$ 或根据位置关系表述为 $BD = DE + CE$($B$,$C$ 在 $AE$ 异侧且 $D$,$E$ 在 $A$ 两侧),$BD = |DE - CE|$($B$,$C$ 在 $AE$ 同侧),简洁语言为 $BD$ 等于 $DE$ 与 $CE$ 的和或差的绝对值,根据位置确定和差。
【答案】:
(1)$BD = DE + CE$;
(2)$BD = DE - CE$;
(3)$BD = CE - DE$;
(4)$BD$ 等于 $DE$ 与 $CE$ 的和或差(根据直线 $AE$ 位置确定)
(1) 因为 $\angle BAC = 90^{\circ}$,所以 $\angle BAD + \angle CAE = 90^{\circ}$。又因为 $BD \perp AE$,$CE \perp AE$,所以 $\angle ADB = \angle AEC = 90^{\circ}$,$\angle BAD + \angle ABD = 90^{\circ}$,故 $\angle ABD = \angle CAE$。在 $\triangle ABD$ 和 $\triangle CAE$ 中,$\angle ADB = \angle AEC$,$\angle ABD = \angle CAE$,$AB = AC$,所以 $\triangle ABD \cong \triangle CAE(AAS)$,则 $BD = AE$,$AD = CE$。因为 $AE = AD + DE = CE + DE$,所以 $BD = DE + CE$。
(2) 同理,$\angle BAC = 90^{\circ}$ 得 $\angle BAD + \angle CAE = 90^{\circ}$,$BD \perp AE$ 得 $\angle BAD + \angle ABD = 90^{\circ}$,所以 $\angle ABD = \angle CAE$。$\triangle ABD \cong \triangle CAE(AAS)$,$BD = AE$,$AD = CE$。此时 $AE = DE - AD = DE - CE$,所以 $BD = DE - CE$。
(3) 由旋转性质及全等三角形可得 $BD = CE - DE$。
(4) 综合三种情况,当 $B$,$C$ 在 $AE$ 异侧且 $D$,$E$ 在 $A$ 两侧时 $BD = DE + CE$;同侧时,若 $BD < CE$ 则 $BD = DE - CE$,若 $BD > CE$ 则 $BD = CE - DE$,统一为 $BD = |DE - CE|$ 或根据位置关系表述为 $BD = DE + CE$($B$,$C$ 在 $AE$ 异侧且 $D$,$E$ 在 $A$ 两侧),$BD = |DE - CE|$($B$,$C$ 在 $AE$ 同侧),简洁语言为 $BD$ 等于 $DE$ 与 $CE$ 的和或差的绝对值,根据位置确定和差。
【答案】:
(1)$BD = DE + CE$;
(2)$BD = DE - CE$;
(3)$BD = CE - DE$;
(4)$BD$ 等于 $DE$ 与 $CE$ 的和或差(根据直线 $AE$ 位置确定)
查看更多完整答案,请扫码查看


