2025年复习大本营期末假期复习一本通暑假八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年复习大本营期末假期复习一本通暑假八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
如图(1),$MA_{1}// NA_{2}$,则$∠A_{1}+∠A_{2}= $
如图(2),$MA_{1}// NA_{3}$,则$∠A_{1}+∠A_{2}+∠A_{3}= $
如图(3),$MA_{1}// NA_{4}$,则$∠A_{1}+∠A_{2}+∠A_{3}+∠A_{4}= $
如图(4),$MA_{1}// NA_{5}$,则$∠A_{1}+∠A_{2}+∠A_{3}+∠A_{4}+∠A_{5}= $
从上述结论中你发现的规律填一填。
如图(5),$MA_{1}// NA_{n}$,则$∠A_{1}+∠A_{2}+∠A_{3}+... +∠A_{n}= $
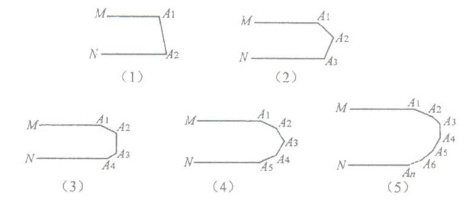
180
度;如图(2),$MA_{1}// NA_{3}$,则$∠A_{1}+∠A_{2}+∠A_{3}= $
360
度;如图(3),$MA_{1}// NA_{4}$,则$∠A_{1}+∠A_{2}+∠A_{3}+∠A_{4}= $
540
度;如图(4),$MA_{1}// NA_{5}$,则$∠A_{1}+∠A_{2}+∠A_{3}+∠A_{4}+∠A_{5}= $
720
度。从上述结论中你发现的规律填一填。
如图(5),$MA_{1}// NA_{n}$,则$∠A_{1}+∠A_{2}+∠A_{3}+... +∠A_{n}= $
$(n-1)×180$
度。
答案:
【解析】:
第一个图:学过的平行线性质,两直线平行,同旁内角互补,
所以,$∠A_{1}+∠A_{2}= 180^\circ$。
第二个图:过$A_{2}$作$A_{2}C// MA_{1}$,
根据平行线的性质:两直线平行,同旁内角互补,
得到$∠A_{1}+∠CA_{2}A_{1}=180^\circ$,$∠A_{2}+∠A_{2}A_{3}C=180^\circ$,
所以,$∠A_{1}+∠A_{2}+∠A_{3}=360^\circ$。
第三个图:过$A_{2}$作$A_{2}C// MA_{1}$,$A_{2}D// NA_{4}$,
根据平行线的性质:两直线平行,同旁内角互补,
得到$∠A_{1}+∠BA_{2}A_{1}=180^\circ$,$∠BA_{2}A_{3}+∠DA_{2}A_{3}=180^\circ$,$∠A_{3}+∠A_{3}A_{4}D=180^\circ$,
所以,$∠A_{1}+∠A_{2}+∠A_{3}+∠A_{4}=540^\circ$。
第四个图:过$A_{2}$作$A_{2}C// MA_{1}$,$A_{2}D// NA_{5}$,过$A_{4}$作$A_{4}E// NA_{5}$,
根据平行线的性质:两直线平行,同旁内角互补,
得到$∠A_{1}+∠CA_{2}A_{1}=180^\circ$,$∠BA_{2}A_{3}+∠DA_{2}A_{3}=180^\circ$,$∠A_{3}+∠DA_{4}E=180^\circ$,$∠EA_{4}A_{5}+∠A_{5}=180^\circ$,
所以,$∠A_{1}+∠A_{2}+∠A_{3}+∠A_{4}+∠A_{5}=720^\circ$。
第五个图:
规律:第一个图是两个角相加是$180^\circ$,以后每增加一个角,和就增加$180^\circ$,
如果有$n$个角,那么和为$(n-1)×180^\circ$,
所以,$∠A_{1}+∠A_{2}+∠A_{3}+\cdots+∠A_{n}=(n-1)×180^\circ$。
【答案】:
$180$;$360$;$540$;$720$;$(n-1)×180$
第一个图:学过的平行线性质,两直线平行,同旁内角互补,
所以,$∠A_{1}+∠A_{2}= 180^\circ$。
第二个图:过$A_{2}$作$A_{2}C// MA_{1}$,
根据平行线的性质:两直线平行,同旁内角互补,
得到$∠A_{1}+∠CA_{2}A_{1}=180^\circ$,$∠A_{2}+∠A_{2}A_{3}C=180^\circ$,
所以,$∠A_{1}+∠A_{2}+∠A_{3}=360^\circ$。
第三个图:过$A_{2}$作$A_{2}C// MA_{1}$,$A_{2}D// NA_{4}$,
根据平行线的性质:两直线平行,同旁内角互补,
得到$∠A_{1}+∠BA_{2}A_{1}=180^\circ$,$∠BA_{2}A_{3}+∠DA_{2}A_{3}=180^\circ$,$∠A_{3}+∠A_{3}A_{4}D=180^\circ$,
所以,$∠A_{1}+∠A_{2}+∠A_{3}+∠A_{4}=540^\circ$。
第四个图:过$A_{2}$作$A_{2}C// MA_{1}$,$A_{2}D// NA_{5}$,过$A_{4}$作$A_{4}E// NA_{5}$,
根据平行线的性质:两直线平行,同旁内角互补,
得到$∠A_{1}+∠CA_{2}A_{1}=180^\circ$,$∠BA_{2}A_{3}+∠DA_{2}A_{3}=180^\circ$,$∠A_{3}+∠DA_{4}E=180^\circ$,$∠EA_{4}A_{5}+∠A_{5}=180^\circ$,
所以,$∠A_{1}+∠A_{2}+∠A_{3}+∠A_{4}+∠A_{5}=720^\circ$。
第五个图:
规律:第一个图是两个角相加是$180^\circ$,以后每增加一个角,和就增加$180^\circ$,
如果有$n$个角,那么和为$(n-1)×180^\circ$,
所以,$∠A_{1}+∠A_{2}+∠A_{3}+\cdots+∠A_{n}=(n-1)×180^\circ$。
【答案】:
$180$;$360$;$540$;$720$;$(n-1)×180$
1. (汕尾)如图,能判定$EB// AC$的条件的是(
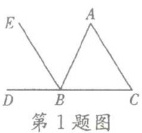
A.$∠C= ∠ABE$
B.$∠A= ∠EBD$
C.$∠C= ∠ABC$
D.$∠A= ∠ABE$
D
)
A.$∠C= ∠ABE$
B.$∠A= ∠EBD$
C.$∠C= ∠ABC$
D.$∠A= ∠ABE$
答案:
【解析】:要判定$EB// AC$,需要找到同位角相等、内错角相等或同旁内角互补的条件。
选项A:$∠C$与$∠ABE$,$∠C$是直线$AC$与$BC$被$DC$所截形成的角,$∠ABE$是直线$EB$与$AB$被$EB$所截形成的角,它们不是同位角、内错角或同旁内角,无法判定平行。
选项B:$∠A$与$∠EBD$,$∠A$是直线$AC$与$AB$被$AC$所截形成的角,$∠EBD$是直线$EB$与$DC$被$EB$所截形成的角,位置关系不符,不能判定平行。
选项C:$∠C=∠ABC$,这两个角是$\triangle ABC$的内角,只能说明$\triangle ABC$是等腰三角形($AB=AC$),与$EB// AC$无关。
选项D:$∠A=∠ABE$,$∠A$和$∠ABE$是直线$AC$与$EB$被直线$AB$所截形成的内错角。根据内错角相等,两直线平行,可判定$EB// AC$。
【答案】:D
选项A:$∠C$与$∠ABE$,$∠C$是直线$AC$与$BC$被$DC$所截形成的角,$∠ABE$是直线$EB$与$AB$被$EB$所截形成的角,它们不是同位角、内错角或同旁内角,无法判定平行。
选项B:$∠A$与$∠EBD$,$∠A$是直线$AC$与$AB$被$AC$所截形成的角,$∠EBD$是直线$EB$与$DC$被$EB$所截形成的角,位置关系不符,不能判定平行。
选项C:$∠C=∠ABC$,这两个角是$\triangle ABC$的内角,只能说明$\triangle ABC$是等腰三角形($AB=AC$),与$EB// AC$无关。
选项D:$∠A=∠ABE$,$∠A$和$∠ABE$是直线$AC$与$EB$被直线$AB$所截形成的内错角。根据内错角相等,两直线平行,可判定$EB// AC$。
【答案】:D
2. (德州)如图,$AD是∠EAC$的平分线,$AD// BC$,$∠B= 30^{\circ }$,则$∠C$为(
A.$30^{\circ }$
B.$60^{\circ }$
C.$80^{\circ }$
D.$120^{\circ }$
A
)
A.$30^{\circ }$
B.$60^{\circ }$
C.$80^{\circ }$
D.$120^{\circ }$
答案:
【解析】:因为AD//BC,且∠B=30°,根据两直线平行,同位角相等,所以∠EAD=∠B=30°。
又因为AD是∠EAC的平分线,所以∠EAC=2∠EAD=2×30°=60°。
∠EAC是△ABC的外角,根据三角形外角等于不相邻的两个内角之和,可得∠EAC=∠B+∠C。
因此,∠C=∠EAC - ∠B=60° - 30°=30°。
【答案】:A
又因为AD是∠EAC的平分线,所以∠EAC=2∠EAD=2×30°=60°。
∠EAC是△ABC的外角,根据三角形外角等于不相邻的两个内角之和,可得∠EAC=∠B+∠C。
因此,∠C=∠EAC - ∠B=60° - 30°=30°。
【答案】:A
3. (丽水)如图,直线$a// b$,$AC⊥AB$,$AC交直线b于点C$,$∠1= 60^{\circ }$,则$∠2$的度数是(

A.$50^{\circ }$
B.$45^{\circ }$
C.$35^{\circ }$
D.$30^{\circ }$
D
)
A.$50^{\circ }$
B.$45^{\circ }$
C.$35^{\circ }$
D.$30^{\circ }$
答案:
【解析】:
由于$ a // b $,根据平行线的性质,$\angle 1$和$\angle ACB$是同位角,所以$\angle 1 = \angle ACB = 60^\circ$。
已知$AC \perp AB$,所以$\angle BAC = 90^\circ$。
在$\triangle ABC$中,内角和为$180^\circ$,所以$\angle 2 = 180^\circ - \angle BAC - \angle ACB = 180^\circ - 90^\circ - 60^\circ = 30^\circ$。
【答案】:D
由于$ a // b $,根据平行线的性质,$\angle 1$和$\angle ACB$是同位角,所以$\angle 1 = \angle ACB = 60^\circ$。
已知$AC \perp AB$,所以$\angle BAC = 90^\circ$。
在$\triangle ABC$中,内角和为$180^\circ$,所以$\angle 2 = 180^\circ - \angle BAC - \angle ACB = 180^\circ - 90^\circ - 60^\circ = 30^\circ$。
【答案】:D
4. (滨州)如图所示,是我们学过的用直尺和三角尺画平行线的方法示意图。画图的原理是(
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.两直线平行,内错角相等
A
)A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.两直线平行,内错角相等
答案:
【解析】:用直尺和三角尺画平行线时,三角尺的一个角在直尺边缘固定,移动三角尺后,这个角的位置发生变化,但角的大小不变。此时,三角尺的同一个角在两条直线被直尺(截线)所截的位置形成了同位角,因为这两个同位角是同一个三角尺的角,所以度数相等。根据“同位角相等,两直线平行”的判定定理,可得出所画的两条直线平行。图中∠EAB和∠ACF是同位角,且它们相等,从而判定直线a与直线b平行。
【答案】:A
【答案】:A
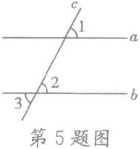
5. (宜宾)如图,直线$a$,$b被第三条直线c$所截,如果$a// b$,$∠1= 70^{\circ }$,那么$∠3$的度数是
70°
。
答案:
【解析】:因为直线$a// b$,$∠1 = 70^{\circ}$,$∠1$与$∠2$是对顶角,所以$∠1=∠2 = 70^{\circ}$。又因为$a// b$,$∠2$与$∠3$是同位角,根据两直线平行,同位角相等,可得$∠2 = ∠3$,所以$∠3=70^{\circ}$。
【答案】:70°
【答案】:70°
6. (汕尾)已知$a$,$b$,$c$为平面内三条不同直线,若$a⊥b$,$c⊥b$,则$a与c$的位置关系是
平行
。
答案:
【解析】:
由于直线$a$和直线$c$都与直线$b$垂直,根据平面几何的性质,两条都与同一条直线垂直的直线必定平行。但这里需要注意,题目没有给出$a$和$c$是否在同一平面内与$b$相交,若$a$和$c$在$b$的垂线上但不在同一平面(即空间中),则$a$和$c$可能是异面的。但根据题意“$a$,$b$,$c$为平面内三条不同直线”,我们可以确定$a$和$c$在同一平面内。
在同一平面内,如果两条直线都与第三条直线垂直,那么这两条直线必定平行。因此,$a$与$c$平行。
但还需要考虑一种特殊情况,即当$a$和$c$重合时,它们也满足都与$b$垂直的条件。但题目中明确指出$a$,$b$,$c$是三条“不同”的直线,所以$a$与$c$不可能重合。
综上,$a$与$c$的位置关系是平行。
【答案】:平行
由于直线$a$和直线$c$都与直线$b$垂直,根据平面几何的性质,两条都与同一条直线垂直的直线必定平行。但这里需要注意,题目没有给出$a$和$c$是否在同一平面内与$b$相交,若$a$和$c$在$b$的垂线上但不在同一平面(即空间中),则$a$和$c$可能是异面的。但根据题意“$a$,$b$,$c$为平面内三条不同直线”,我们可以确定$a$和$c$在同一平面内。
在同一平面内,如果两条直线都与第三条直线垂直,那么这两条直线必定平行。因此,$a$与$c$平行。
但还需要考虑一种特殊情况,即当$a$和$c$重合时,它们也满足都与$b$垂直的条件。但题目中明确指出$a$,$b$,$c$是三条“不同”的直线,所以$a$与$c$不可能重合。
综上,$a$与$c$的位置关系是平行。
【答案】:平行
7. (杭州)如图,已知直线$a// b$,若$∠1= 40^{\circ }50'$,则$∠2= $

$139^\circ 10'$
。
答案:
【解析】:
由于直线 $a // b$,根据平行线的性质,$\angle 1$ 和 $\angle 2$ 是同旁内角,它们的和为 $180^\circ$。
已知 $\angle 1 = 40^\circ 50'$,则 $\angle 2$ 可以通过以下计算求出:
$\angle 2 = 180^\circ - \angle 1$。
首先将 $180^\circ$ 转换为度和分的形式,即 $180^\circ = 179^\circ 60'$。
然后进行减法运算:
$\angle 2 = 179^\circ 60' - 40^\circ 50' = 139^\circ 10'$。
【答案】:$139^\circ 10'$
由于直线 $a // b$,根据平行线的性质,$\angle 1$ 和 $\angle 2$ 是同旁内角,它们的和为 $180^\circ$。
已知 $\angle 1 = 40^\circ 50'$,则 $\angle 2$ 可以通过以下计算求出:
$\angle 2 = 180^\circ - \angle 1$。
首先将 $180^\circ$ 转换为度和分的形式,即 $180^\circ = 179^\circ 60'$。
然后进行减法运算:
$\angle 2 = 179^\circ 60' - 40^\circ 50' = 139^\circ 10'$。
【答案】:$139^\circ 10'$
查看更多完整答案,请扫码查看


