《2025年复习大本营期末假期复习一本通暑假八年级数学北师大版》

21. 如图所示,$△ABC$为等边三角形,且$∠1= ∠2= ∠3$。
(1)求$∠BEC$的度数。
(2)$△DEF$是等边三角形吗？请说明理由。

答案： 【解析】：
(1)因为△ABC是等边三角形，所以∠ABC=∠ACB=∠BAC=60°，即∠ABC=∠ABE+∠2=60°。又因为∠1=∠2=∠3，所以∠ABE+∠1=60°。在△BEC中，∠BEC=180°-(∠EBC+∠ECB)，而∠EBC=∠ABE，∠ECB=∠3=∠1，所以∠EBC+∠ECB=∠ABE+∠1=60°，因此∠BEC=180°-60°=120°。
(2)由
(1)知∠BEC=120°，同理可得∠ADB=∠CFA=120°。所以∠FDE=180°-∠ADB=180°-120°=60°，∠DEF=180°-∠BEC=180°-120°=60°，∠DFE=180°-∠CFA=180°-120°=60°。因为∠FDE=∠DEF=∠DFE=60°，所以△DEF是等边三角形。
【答案】：
(1)120°；
(2)是，理由见解析

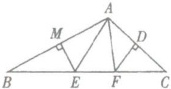
22. 如下图所示,在$△ABC$中,已知AB、AC的垂直平分线分别交BC于点E、F,且$∠BAC= 115^{\circ }$,求$∠EAF$的度数。

答案： 【解析】：
因为$AB$，$AC$的垂直平分线分别交$BC$于点$E$、$F$，
所以$EA=EB$，$FA=FC$，
所以$\angle B=\angle EAB$，$\angle C=\angle FAC$，
在$\triangle ABC$中，$\angle B+\angle C=180^{\circ}-\angle BAC=180^{\circ}-115^{\circ}=65^{\circ}$，
所以$\angle EAB+\angle FAC=\angle B+\angle C=65^{\circ}$，
所以$\angle EAF=\angle BAC-(\angle EAB+\angle FAC)=115^{\circ}-65^{\circ}=50^{\circ}$。
【答案】：$50^{\circ}$

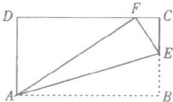
23. 如下图所示,将长方形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处。若$△AFD$的周长为24cm,$△ECF$的周长为8cm,求长方形纸片ABCD的周长。

答案： 【解析】：根据折叠的性质，可得 $AF = AB$，$EF = BE$。
因为 $\triangle AFD$ 的周长为 $24\space cm$，所以 $AD + DF + AF = 24\space cm$。
又因为 $\triangle ECF$ 的周长为 $8\space cm$，所以 $CF + CE + EF = 8\space cm$。
将上述两个等式相加，得到：
$\begin{aligned}AD + DF + AF + CF + CE + EF&=24 + 8\\AD + (DF + CF) + AF + (CE + EF)&=32\end{aligned}$
由于 $DF + CF = DC$，且 $AF = AB$，$CE + EF = CE + BE = BC$，而在长方形 $ABCD$ 中，$AB = DC$，$AD = BC$，所以上式可化简为：
$AD + DC + AB + BC = 32$
即长方形 $ABCD$ 的周长为 $32\space cm$。
【答案】：32

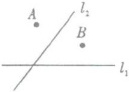
24. 有公路$l_{1}$同侧、$l_{2}$异侧的两个城镇A、B,如下图所示。电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路$l_{1}$,$l_{2}$的距离也必须相等,发射塔C应修建在什么位置？请用尺规作图找出所有符合条件的点,注明点C的位置。(保留作图痕迹,不要求写出画法)

答案： 【解析】：
1. 首先，作出公路$l_1$和$l_2$的夹角平分线。
2. 接着，作出线段$AB$的垂直平分线。
3. 这两条线的交点即为所求的发射塔的位置$C_1$，$C_2$。
根据角平分线的性质，角平分线上的点到角两边的距离相等，所以作出公路$l_1$和$l_2$的夹角平分线，就可以找到到两条公路距离相等的点所在的直线；根据线段垂直平分线的性质，线段垂直平分线上的点到线段两端点的距离相等，所以作出线段$AB$的垂直平分线，就可以找到到$A$、$B$两个城镇距离相等的点所在的直线。两条直线的交点就是同时满足到两个城镇$A$，$B$的距离相等，到两条公路$l_1$，$l_2$的距离也相等的点。
【答案】：
符合条件的点有$C_1$，$C_2$两个点。