《2025年复习大本营期末假期复习一本通暑假八年级数学北师大版》

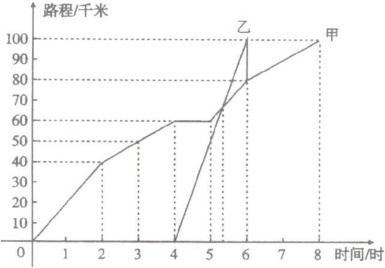
4. 甲、乙两人(甲骑自行车,乙骑摩托车)从A城出发到B城旅行,如图表示甲、乙两人离开A城的路程与时间之间的关系,如根据图象,你能得到关于甲、乙两人旅行的哪些信息?(答题要求:至少提供五条信息,如由图象可知:A,B两地相距100千米)

答案： 【解析】：通过观察甲、乙两人离开A城的路程与时间关系图象，可从出发时间、到达时间、行驶过程中的停留情况、相遇时刻以及速度快慢等方面获取信息。从横轴时间和纵轴路程的对应关系分析：甲的图象起点在原点，说明甲0时出发；乙的图象起点在时间4时，路程0千米处，即乙4时出发。甲到达B城（路程100千米）对应的时间是8时，乙到达对应的时间是6时。甲的图象在3 - 4小时段路程未变（从60千米保持），表明甲中途停留1小时。甲和乙的图象交点对应的时间是5小时，此时路程70千米，即5时两人相遇。乙从4时出发到6时到达，用时2小时行100千米，甲从0时到8时（扣除停留1小时实际行驶7小时）行100千米，显然乙速度比甲快。
【答案】：1. 甲0时出发，乙4时出发；2. 甲8时到达B城，乙6时到达B城；3. 甲在3 - 4小时中途停留1小时；4. 5时甲、乙两人相遇，此时距A城70千米；5. 乙的旅行速度比甲快。

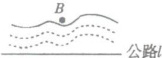
5. 如图,河边有一条笔直的公路l,公路两侧是平坦的草地.在数学活动课上,老师要求测量河对岸B点到公路的距离,请你设计一个测量方案.要求:
(1)列出你测量所使用的测量工具;
(2)画出测量的示意图,写出测量的步骤;
(3)用字母表示测得的数据,求出B点到公路的距离.

答案： 【解析】：要测量河对岸B点到公路l的距离，即测量点B到直线l的垂线段长度。可利用全等三角形或相似三角形的知识，通过在公路同侧构造可测量的三角形来间接求出距离。这里采用构造全等三角形的方法，在公路上选取合适的点，通过测量角度和距离，利用“角边角”（ASA）证明三角形全等，从而得到对应边相等，即B点到公路的距离等于测量出的某条线段长度。
【答案】：
(1)测量工具：皮尺、量角器；
(2)示意图（略，需自行绘制：在公路l上取点A，过A作AC⊥l，在AC延长线上取点D使AC=CD，过D作DE⊥l，在DE上找一点E使B、A、E共线，测量DE长度）；步骤：①在公路l上任取一点A；②用皮尺和量角器过A作AC⊥l，在AC延长线上取点D，使AC=CD（用皮尺量AC长度并标记D）；③过D作DE⊥l（用量角器确保DE⊥l）；④移动E点，使视线B、A、E在同一直线上，用皮尺测量DE的长度，记为m；
(3)B点到公路的距离为m。

6. 袋中装有6个红球,3个白球,1个黄球,这些球除了颜色以外都相同,小明认为袋中共有三种不同颜色的球,所以从袋中任意摸出一球,摸到红球、白球或黄球的可能性是相同的,你认为小明的想法对吗?说说你的理由.

答案： 【解析】：
小明认为从袋中摸出红球、白球或黄球的可能性相同，但这是不正确的。
袋中球的总数为 $6 + 3 + 1 = 10$ 个。
摸到红球的概率为 $\frac{6}{10}$，
摸到白球的概率为 $\frac{3}{10}$，
摸到黄球的概率为 $\frac{1}{10}$。
由于 $\frac{6}{10} \gt \frac{3}{10} \gt \frac{1}{10}$，
因此摸到红球、白球和黄球的可能性并不相同。
【答案】：不对；因为摸到红球、白球和黄球的概率分别为 $\frac{6}{10}$，$\frac{3}{10}$ 和 $\frac{1}{10}$，它们并不相等。