2025年假日时光暑假作业阳光出版社八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假日时光暑假作业阳光出版社八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
17. 先化简,再求值:$(x - 1)^{2}+x(x + 2)$,其中$x= \sqrt{2}$.
答案:
【解析】:首先,我们对原式进行化简。
$\begin{aligned}&(x - 1)^2 + x(x + 2)\\=&x^2 - 2x + 1 + x^2 + 2x\\=&(x^2 + x^2) + (-2x + 2x) + 1\\=&2x^2 + 0 + 1\\=&2x^2 + 1\end{aligned}$
接下来,将$x = \sqrt{2}$代入化简后的式子$2x^2 + 1$中:
$\begin{aligned}&2×(\sqrt{2})^2 + 1\\=&2×2 + 1\\=&4 + 1\\=&5\end{aligned}$
【答案】:5
$\begin{aligned}&(x - 1)^2 + x(x + 2)\\=&x^2 - 2x + 1 + x^2 + 2x\\=&(x^2 + x^2) + (-2x + 2x) + 1\\=&2x^2 + 0 + 1\\=&2x^2 + 1\end{aligned}$
接下来,将$x = \sqrt{2}$代入化简后的式子$2x^2 + 1$中:
$\begin{aligned}&2×(\sqrt{2})^2 + 1\\=&2×2 + 1\\=&4 + 1\\=&5\end{aligned}$
【答案】:5
18. 实数$a,b$在数轴上的位置如图所示,化简$\sqrt{a^{2}}-\sqrt{b^{2}}-\sqrt{(a - b)^{2}}$.
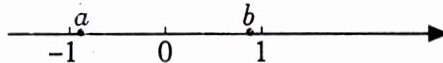
解:由数轴可知:$a < 0$,$b > 0$,$a - b < 0$,
$\sqrt{a^2} - \sqrt{b^2} - \sqrt{(a - b)^2}$
$= |a| - |b| - |a - b|$
$= -a - b + (a - b)$
$= -2b$
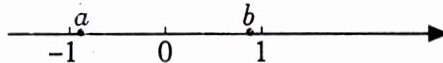
解:由数轴可知:$a < 0$,$b > 0$,$a - b < 0$,
$\sqrt{a^2} - \sqrt{b^2} - \sqrt{(a - b)^2}$
$= |a| - |b| - |a - b|$
$= -a - b + (a - b)$
$= -2b$
答案:
解:由数轴可知:$a < 0$,$b > 0$,$a - b < 0$,
$\sqrt{a^2} - \sqrt{b^2} - \sqrt{(a - b)^2}$
$= |a| - |b| - |a - b|$
$= -a - b + (a - b)$
$= -2b$
$\sqrt{a^2} - \sqrt{b^2} - \sqrt{(a - b)^2}$
$= |a| - |b| - |a - b|$
$= -a - b + (a - b)$
$= -2b$
19. 已知实数$x,y,a$满足:$\sqrt{x + y - 8}+\sqrt{8 - x - y}= \sqrt{3x - y - a}+\sqrt{x - 2y + a + 3}$,试问长度分别为$x,y,a$的三条线段能否构成一个三角形?
答案:
长度分别为$x$,$y$,$a$的三条线段能构成一个三角形。
理由:由被开方数的非负性可得$x + y - 8\geqslant$0,①$8 - x - y\geqslant0$,②$3x - y - a\geqslant0$,③$x - 2y + a + 3\geqslant0$,④
由①②可得$x + y = 8$,⑤ 即$\sqrt{3x - y - a} + \sqrt{x - 2y + a + 3} = 0$,
由非负数的性质可得$\begin{cases}3x - y = a\\x - 2y = -a - 3\end{cases}$,结合⑤式,解得$x = 3$,$y = 5$,$a = 4$。
由于$3 + 4 > 5$,所以可以构成三角形。
理由:由被开方数的非负性可得$x + y - 8\geqslant$0,①$8 - x - y\geqslant0$,②$3x - y - a\geqslant0$,③$x - 2y + a + 3\geqslant0$,④
由①②可得$x + y = 8$,⑤ 即$\sqrt{3x - y - a} + \sqrt{x - 2y + a + 3} = 0$,
由非负数的性质可得$\begin{cases}3x - y = a\\x - 2y = -a - 3\end{cases}$,结合⑤式,解得$x = 3$,$y = 5$,$a = 4$。
由于$3 + 4 > 5$,所以可以构成三角形。
20. 先阅读下面的文字,然后回答问题.
甲、乙两名同学解答题目“先化简,再求值:$a+\sqrt{1 - 2a + a^{2}}$,其中$a = 9$”时得出了不同的答案.
甲同学的解答:原式$=a+\sqrt{(1 - a)^{2}}= a + 1 - a = 1$;
乙同学的解答:原式$=a+\sqrt{(1 - a)^{2}}= a+\vert1 - a\vert=a + a - 1 = 2a - 1 = 2×9 - 1 = 17$.
问题:
甲、乙两名同学解答题目“先化简,再求值:$a+\sqrt{1 - 2a + a^{2}}$,其中$a = 9$”时得出了不同的答案.
甲同学的解答:原式$=a+\sqrt{(1 - a)^{2}}= a + 1 - a = 1$;
乙同学的解答:原式$=a+\sqrt{(1 - a)^{2}}= a+\vert1 - a\vert=a + a - 1 = 2a - 1 = 2×9 - 1 = 17$.
问题:
甲同学
的解答是错误的,错误的原因是什么?
答案:
甲同学。
解:原式$=a + \sqrt{(1 - a)^2} = a + |1 - a|$。当$a = 9$时,$1 - a = -8 < 0$,所以$|1 - a| = a - 1$,则原式$=a + a - 1 = 2a - 1$。甲同学未正确理解$\sqrt{a^2}=|a|$,直接取$\sqrt{(1 - a)^2}=1 - a$,导致错误。
解:原式$=a + \sqrt{(1 - a)^2} = a + |1 - a|$。当$a = 9$时,$1 - a = -8 < 0$,所以$|1 - a| = a - 1$,则原式$=a + a - 1 = 2a - 1$。甲同学未正确理解$\sqrt{a^2}=|a|$,直接取$\sqrt{(1 - a)^2}=1 - a$,导致错误。
想想看,巴霍姆应该怎样行走才能获得最多的土地?
19世纪俄国文学巨匠列夫·托尔斯泰曾在作品《一个人需要很多土地吗》中写了这样一个故事:
有一个叫巴霍姆的人到草原上去购买土地,卖地的酋长出了一个非常奇怪的地价“每天$1000$卢布”,意思是谁出$1000$卢布,只要他日出时从规定地点出发,日落前返回出发点,所走过的路线圈起的土地就全部归他.如果日落前不能回到出发点,那么他就得不到半点土地,白出$1000$卢布.
巴霍姆觉得这个条件对自己有利,便付了$1000$卢布.第二天天刚亮,他就连忙在草原上大步向前走去.他走了足足有$10$俄里($1俄里\approx1.0668$公里),才朝左拐弯;接着又走了许久,才再向左拐弯;这样又走了$2$俄里,这时他发现天色不早,而自己离出发点还足有$15$俄里的路程,于是只得改变方向,径直朝出发点奔去……最后,他总算如期回到了出发点,却因过度劳累,口吐鲜血而死.
请你算一算,巴霍姆这一天走了多少俄里路?他走过的路线围成的土地面积有多大?(结果保留二次根式)
19世纪俄国文学巨匠列夫·托尔斯泰曾在作品《一个人需要很多土地吗》中写了这样一个故事:
有一个叫巴霍姆的人到草原上去购买土地,卖地的酋长出了一个非常奇怪的地价“每天$1000$卢布”,意思是谁出$1000$卢布,只要他日出时从规定地点出发,日落前返回出发点,所走过的路线圈起的土地就全部归他.如果日落前不能回到出发点,那么他就得不到半点土地,白出$1000$卢布.
巴霍姆觉得这个条件对自己有利,便付了$1000$卢布.第二天天刚亮,他就连忙在草原上大步向前走去.他走了足足有$10$俄里($1俄里\approx1.0668$公里),才朝左拐弯;接着又走了许久,才再向左拐弯;这样又走了$2$俄里,这时他发现天色不早,而自己离出发点还足有$15$俄里的路程,于是只得改变方向,径直朝出发点奔去……最后,他总算如期回到了出发点,却因过度劳累,口吐鲜血而死.
请你算一算,巴霍姆这一天走了多少俄里路?他走过的路线围成的土地面积有多大?(结果保留二次根式)
答案:
【解析】:根据题意,巴霍姆行走的路线是一个四边形,其中三次拐弯均向左,可判断该四边形为直角梯形(前两次拐弯形成直角,第三次拐弯后走向出发点)。设他第一次走的路程为$a = 10$俄里,第三次走的路程为$b = 2$俄里,最后返回出发点的路程为$c = 15$俄里,第二次走的路程为$x$俄里。
由于前两次拐弯为直角,第二次行走的路程$x$与最后返回的路程$c$构成直角三角形的斜边,两条直角边分别为$(a - b)$和$x$。根据勾股定理可得:$x^2 + (a - b)^2 = c^2$,即$x^2 + (10 - 2)^2 = 15^2$,解得$x = \sqrt{15^2 - 8^2} = \sqrt{225 - 64} = \sqrt{161}$俄里。
总路程为四次行走路程之和:$a + x + b + c = 10 + \sqrt{161} + 2 + 15 = 27 + \sqrt{161}$俄里。
围成的土地面积为直角梯形的面积,上底为$b = 2$俄里,下底为$a = 10$俄里,高为第二次行走的路程$x = \sqrt{161}$俄里,面积$S = \frac{(a + b) × x}{2} = \frac{(10 + 2) × \sqrt{161}}{2} = 6\sqrt{161}$平方俄里。
【答案】:巴霍姆这一天走了$27 + \sqrt{161}$俄里路,走过的路线围成的土地面积是$6\sqrt{161}$平方俄里。
由于前两次拐弯为直角,第二次行走的路程$x$与最后返回的路程$c$构成直角三角形的斜边,两条直角边分别为$(a - b)$和$x$。根据勾股定理可得:$x^2 + (a - b)^2 = c^2$,即$x^2 + (10 - 2)^2 = 15^2$,解得$x = \sqrt{15^2 - 8^2} = \sqrt{225 - 64} = \sqrt{161}$俄里。
总路程为四次行走路程之和:$a + x + b + c = 10 + \sqrt{161} + 2 + 15 = 27 + \sqrt{161}$俄里。
围成的土地面积为直角梯形的面积,上底为$b = 2$俄里,下底为$a = 10$俄里,高为第二次行走的路程$x = \sqrt{161}$俄里,面积$S = \frac{(a + b) × x}{2} = \frac{(10 + 2) × \sqrt{161}}{2} = 6\sqrt{161}$平方俄里。
【答案】:巴霍姆这一天走了$27 + \sqrt{161}$俄里路,走过的路线围成的土地面积是$6\sqrt{161}$平方俄里。
查看更多完整答案,请扫码查看


