《2025年假日时光暑假作业阳光出版社八年级数学人教版》

26. (8分)计算:
(1)$(\sqrt{5} - 2)^2 + 5\sqrt{10} ÷ \sqrt{2} - 9$;
(2)$\sqrt{\frac{2}{3}} ÷ \sqrt{2\frac{2}{3}} × \sqrt{\frac{2}{5}}$.

答案：
(1)原式$=5-4\sqrt{5}+4+5\sqrt{10}÷2-9$
$=5-4\sqrt{5}+4+5\sqrt{5}-9=\sqrt{5}$.
(2)原式$=\sqrt{\frac{2}{3}×\frac{3}{8}×\frac{2}{5}}=\frac{\sqrt{10}}{10}$.

27. (6分)如图,在四边形$ABCD$中,$\angle ADC = 90^{\circ},AD = 4\mathrm{cm},CD = 3\mathrm{cm},AB = 13\mathrm{cm},BC = 12\mathrm{cm}$,求这个四边形的面积.

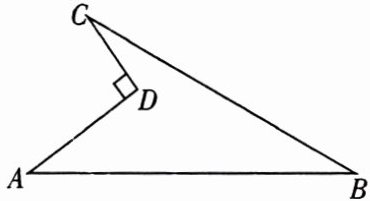
连接 AC,$\because AD=4cm,CD=3cm,∠ADC=90^{\circ },$$\therefore AC=\sqrt{CD^{2}+AD^{2}}=\sqrt{3^{2}+4^{2}}=$5$(cm)$,$\therefore S_{△ACD}=\frac{1}{2}CD\cdot AD=$6$cm^{2}$.在$△ABC$中,$\because 5^{2}+12^{2}=13^{2}$,即$AC^{2}+BC^{2}=AB^{2},\therefore △ABC$为直角三角形,即$∠ACB=90^{\circ },\therefore S_{△ABC}=\frac{1}{2}AC\cdot BC=$30$cm^{2}$.$\therefore S_{四边形ABCD}=S_{△ABC}+S_{△ACD}=$30+6=36$(cm^{2})$.答:四边形 ABCD 的面积为36$cm^{2}$.

答案： 连接 AC,$\because AD=4cm,CD=3cm,∠ADC=90^{\circ },$
$\therefore AC=\sqrt{CD^{2}+AD^{2}}=\sqrt{3^{2}+4^{2}}=5(cm),$
$\therefore S_{△ACD}=\frac{1}{2}CD\cdot AD=6cm^{2}$.
在$△ABC$中,$\because 5^{2}+12^{2}=13^{2}$,即$AC^{2}+BC^{2}=AB^{2},\therefore △ABC$为直角三角形,即$∠ACB=90^{\circ },\therefore S_{△ABC}=\frac{1}{2}AC\cdot BC=30cm^{2}$.
$\therefore S_{四边形ABCD}=S_{△ABC}-S_{△ACD}=30-6=24(cm^{2})$.
答:四边形 ABCD 的面积为$24cm^{2}$.