2025年假日时光暑假作业阳光出版社八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假日时光暑假作业阳光出版社八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列四组线段中,可以构成直角三角形的是(
A.4,5,6
B.1.5,2,2.5
C.2,3,4
D.$1,\sqrt {2},3$
B
)A.4,5,6
B.1.5,2,2.5
C.2,3,4
D.$1,\sqrt {2},3$
答案:
B
2. a、b、c 是$△ABC$的三边长,$△ABC$在下列条件下,不是直角三角形的是(
A.$b^{2}= a^{2}-c^{2}$
B.$a:b:c= 1:\sqrt {3}:2$
C.$∠A:∠B:∠C= 1:2:3$
D.$∠A= 30^{\circ },AB:AC= 1:2$
D
)A.$b^{2}= a^{2}-c^{2}$
B.$a:b:c= 1:\sqrt {3}:2$
C.$∠A:∠B:∠C= 1:2:3$
D.$∠A= 30^{\circ },AB:AC= 1:2$
答案:
D
3. 三角形的两边长为 3 和 4,要使三角形为直角三角形,那么第三边长为(
A.5
B.$\sqrt {5}$
C.$\sqrt {7}$
D.5或$\sqrt {7}$
D
)A.5
B.$\sqrt {5}$
C.$\sqrt {7}$
D.5或$\sqrt {7}$
答案:
D
4. 下列定理中,有逆定理的个数是(
①有两边相等的三角形是等腰三角形;②若三角形三边长 a、b、c 满足$a^{2}+b^{2}= c^{2}$,则该三角形是直角三角形;③全等三角形对应角相等;④若$a= b$,则$a^{2}= b^{2}.$
A.1
B.2
C.3
D.4
B
)①有两边相等的三角形是等腰三角形;②若三角形三边长 a、b、c 满足$a^{2}+b^{2}= c^{2}$,则该三角形是直角三角形;③全等三角形对应角相等;④若$a= b$,则$a^{2}= b^{2}.$
A.1
B.2
C.3
D.4
答案:
B
5. 五根小木棒,其长度(单位:cm)分别为7,15,20,24,25.现将它们摆成两个直角三角形,其中正确的是(
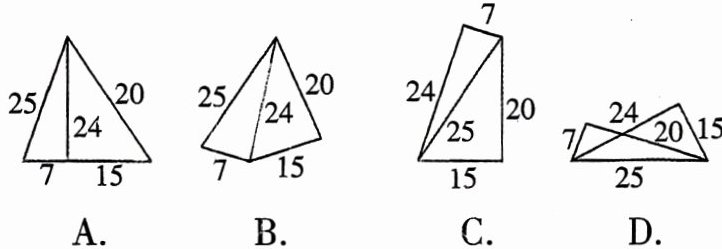
C
)
答案:
C
6. 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则$∠ABC$的度数为(
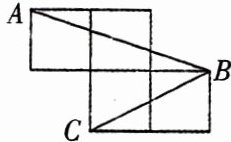
A.$90^{\circ }$
B.$60^{\circ }$
C.$45^{\circ }$
D.$30^{\circ }$
C
)
A.$90^{\circ }$
B.$60^{\circ }$
C.$45^{\circ }$
D.$30^{\circ }$
答案:
C
7. 命题“若$|a|= |b|$,则$a^{2}= b^{2}$”的逆命题是
若$a^{2}=b^{2}$,则$|a|=|b|$
,它是真
命题(填“真”或“假”).
答案:
若$a^{2}=b^{2}$,则$|a|=|b|$真
8. 在$△ABC$中,若$AB= \sqrt {2},AC= \sqrt {2},BC= 2$,则$∠B= $
45
度.
答案:
45
9. 在$△ABC$中,$AB= 12cm,AC= 5cm,BC= 13cm$,则 BC 边上的高$AD= $
$\frac{60}{13}$
cm.
答案:
$\frac{60}{13}$
10. 已知 a,b,c 是$△ABC$三边的长,且满足关系式$\sqrt {c^{2}-a^{2}-b^{2}}+|a-b|= 0$,则$△ABC$的形状为
等腰直角三角形
.
答案:
等腰直角三角形
11. 一个三角形的三边长之比为$5:12:13$,且周长是 60,则它的面积是____
120
.
答案:
120
12. 判断满足下列条件的三角形是否为直角三角形.
(1)在$△ABC$中,$∠A= 20^{\circ },∠B= 70^{\circ };$
(2)在$△ABC$中,$AC= 7,AB= 24,BC= 25;$
(3)一个三角形的三边长 a、b、c 满足$(a+b)\cdot (a-b)= c^{2}.$
(1)在$△ABC$中,$∠A= 20^{\circ },∠B= 70^{\circ };$
是直角三角形
(2)在$△ABC$中,$AC= 7,AB= 24,BC= 25;$
是直角三角形
(3)一个三角形的三边长 a、b、c 满足$(a+b)\cdot (a-b)= c^{2}.$
是直角三角形
答案:
(1)在$\triangle ABC$中,$\because ∠A = 20^{\circ}$,$∠B = 70^{\circ}$,
$\therefore ∠C = 180^{\circ}-∠A - ∠B = 90^{\circ}$,即$\triangle ABC$是直角三角形。
(2)$\because AC^{2}+AB^{2}=7^{2}+24^{2}=625$,$BC^{2}=25^{2}=625$,$\therefore AC^{2}+AB^{2}=BC^{2}$。
根据勾股定理的逆定理可知,$\triangle ABC$是直角三角形。
(3)$\because (a + b)(a - b)=c^{2}$,$\therefore a^{2}-b^{2}=c^{2}$,即$a^{2}=b^{2}+c^{2}$。
根据勾股定理的逆定理可知,$\triangle ABC$是直角三角形。
(1)在$\triangle ABC$中,$\because ∠A = 20^{\circ}$,$∠B = 70^{\circ}$,
$\therefore ∠C = 180^{\circ}-∠A - ∠B = 90^{\circ}$,即$\triangle ABC$是直角三角形。
(2)$\because AC^{2}+AB^{2}=7^{2}+24^{2}=625$,$BC^{2}=25^{2}=625$,$\therefore AC^{2}+AB^{2}=BC^{2}$。
根据勾股定理的逆定理可知,$\triangle ABC$是直角三角形。
(3)$\because (a + b)(a - b)=c^{2}$,$\therefore a^{2}-b^{2}=c^{2}$,即$a^{2}=b^{2}+c^{2}$。
根据勾股定理的逆定理可知,$\triangle ABC$是直角三角形。
13. 如图,在$△ABC$中,$AB= 5,AC= 13$,BC 边上的中线$AD= 6$,求 BC 的长.
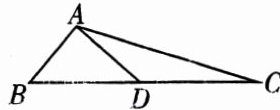
BC的长为

BC的长为
$2\sqrt{61}$
.
答案:
延长$AD$到点$M$,使$DM = AD$,则$AM = 2AD = 12$。连接$CM$,易得$\triangle ABD\cong\triangle MCD$,$\therefore AB = CM = 5$。
在$\triangle ACM$中,$5^{2}+12^{2}=13^{2}$,即$CM^{2}+AM^{2}=AC^{2}$,$\therefore ∠AMC = 90^{\circ}$。
在$Rt\triangle DCM$中,$CD=\sqrt{CM^{2}+DM^{2}}=\sqrt{5^{2}+6^{2}}=\sqrt{61}$,
$\therefore BC = 2CD = 2\sqrt{61}$。
在$\triangle ACM$中,$5^{2}+12^{2}=13^{2}$,即$CM^{2}+AM^{2}=AC^{2}$,$\therefore ∠AMC = 90^{\circ}$。
在$Rt\triangle DCM$中,$CD=\sqrt{CM^{2}+DM^{2}}=\sqrt{5^{2}+6^{2}}=\sqrt{61}$,
$\therefore BC = 2CD = 2\sqrt{61}$。
查看更多完整答案,请扫码查看


