《2025年假日时光暑假作业阳光出版社八年级数学人教版》

12. 如图,已知$□ ABCD$中,对角线 AC 的垂直平分线 EF 交 AD、BC 于点 E、F.
求证:四边形 AFCE 为菱形.
证明：
∵EF垂直平分AC，
∴AE=CE，OA=OC，∠AOE=∠COF=90°。
∵四边形ABCD是平行四边形，
∴AD//BC，
∴∠1=∠3（两直线平行，内错角相等）。
在△AOE和△COF中，
$\left\{\begin{array}{l} ∠1=∠3 \\ OA=OC \\ ∠AOE=∠COF \end{array}\right.$，
∴△AOE≌△COF（ASA），
∴AE=CF。
∵AE//CF，
∴四边形AFCE是平行四边形。
∵EF⊥AC，
∴平行四边形AFCE是菱形。

答案： 证明：
∵EF垂直平分AC，
∴AE=CE，OA=OC，∠AOE=∠COF=90°。
∵四边形ABCD是平行四边形，
∴AD//BC，
∴∠1=∠3（两直线平行，内错角相等）。
在△AOE和△COF中，
$\left\{\begin{array}{l} ∠1=∠3 \\ OA=OC \\ ∠AOE=∠COF \end{array}\right.$，
∴△AOE≌△COF（ASA），
∴AE=CF。
∵AE//CF，
∴四边形AFCE是平行四边形。
∵EF⊥AC，
∴平行四边形AFCE是菱形。

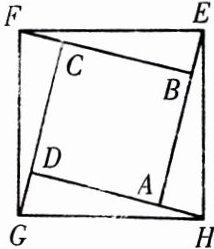
13. 已知:如图,顺次延长正方形 ABCD 的各边 AB、BC、CD、DA 至 E、F、G、H,且使$BE = CF = DG = AH$.
求证:四边形 EFGH 是正方形.

证明：
∵四边形$ABCD$为正方形，
∴$AB = BC = CD = DA$，$\angle ABC = \angle BCD = \angle CDA = \angle DAB = 90^{\circ}$，
∴$\angle FCG = \angle HDG = \angle EAH = \angle FBE = 90^{\circ}$。
∵$BE = CF = DG = AH$，
∴$AB + BE = BC + CF = CD + DG = DA + AH$，即$AE = BF = CG = DH$。
在$\triangle EBF$、$\triangle FCG$、$\triangle GDH$和$\triangle HAE$中，
$\begin{cases} BE = CF = DG = AH \\ \angle FBE = \angle FCG = \angle HDG = \angle EAH = 90^{\circ} \\ BF = CG = DH = AE \end{cases}$，
∴$\triangle EBF \cong \triangle FCG \cong \triangle GDH \cong \triangle HAE$(SAS)，
∴$EF = FG = GH = HE$，$\angle BEF = \angle CFG = \angle DGH = \angle AHE$。
∵$\angle BEF + \angle BFE = 90^{\circ}$，且$\angle BFE = \angle CGF$，
∴$\angle BEF + \angle CGF = 90^{\circ}$，
∴$\angle EFG = 180^{\circ} - (\angle BEF + \angle CGF) = 90^{\circ}$。
同理可证$\angle FGH = \angle GHE = \angle HEF = 90^{\circ}$，
∴四边形$EFGH$是正方形。

答案： 证明：
∵四边形$ABCD$为正方形，
∴$AB = BC = CD = DA$，$\angle ABC = \angle BCD = \angle CDA = \angle DAB = 90^{\circ}$，
∴$\angle FCG = \angle HDG = \angle EAH = \angle FBE = 90^{\circ}$。
∵$BE = CF = DG = AH$，
∴$AB + BE = BC + CF = CD + DG = DA + AH$，即$AE = BF = CG = DH$。
在$\triangle EBF$、$\triangle FCG$、$\triangle GDH$和$\triangle HAE$中，
$\begin{cases} BE = CF = DG = AH \\ \angle FBE = \angle FCG = \angle HDG = \angle EAH = 90^{\circ} \\ BF = CG = DH = AE \end{cases}$，
∴$\triangle EBF \cong \triangle FCG \cong \triangle GDH \cong \triangle HAE(SAS)$，
∴$EF = FG = GH = HE$，$\angle BEF = \angle CFG = \angle DGH = \angle AHE$。
∵$\angle BEF + \angle BFE = 90^{\circ}$，且$\angle BFE = \angle CGF$，
∴$\angle BEF + \angle CGF = 90^{\circ}$，
∴$\angle EFG = 180^{\circ} - (\angle BEF + \angle CGF) = 90^{\circ}$。
同理可证$\angle FGH = \angle GHE = \angle HEF = 90^{\circ}$，
∴四边形$EFGH$是正方形。

14. 如图所示,在$□ ABCD$中,$AB⊥AC$,$AB = 1$,$BC = \sqrt {5}$,对角线 AC,BD 交于点 O,将直线 AC 绕点 O 顺时针旋转,分别交 BC,AD 于点 E,F,连接 BF,DE.
(1)试证明在旋转过程中,线段 AF 与 EC 总保持相等.
证明：$\because$四边形$ABCD$为平行四边形，$\therefore AO = CO$，$\angle FAO = \angle ECO$。又$\angle AOF = \angle COE$，$\therefore \triangle AOF\cong \triangle COE$，$\therefore AF = EC$。
(2)在旋转过程中,四边形 BEDF 有可能是菱形吗? 请说明理由.
四边形$BEDF$有可能是菱形，理由如下：由(1)知，$\triangle AOF\cong \triangle COE$，得$OE = OF$，又$OB = OD$，$\therefore EF$与$BD$互相平分。当$EF\perp BD$时，四边形$BEDF$为菱形。

答案：
(1)$\because$四边形$ABCD$为平行四边形，$\therefore AO = CO$，$\angle FAO = \angle ECO$。又$\angle AOF = \angle COE$，$\therefore \triangle AOF\cong \triangle COE$，$\therefore AF = EC$。
(2)四边形$BEDF$有可能是菱形，理由如下：由
(1)知，$\triangle AOF\cong \triangle COE$，得$OE = OF$，又$OB = OD$，$\therefore EF$与$BD$互相平分。当$EF\perp BD$时，四边形$BEDF$为菱形。

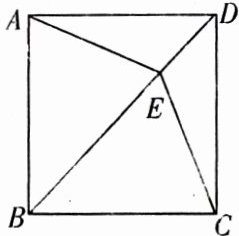
15. 已知:如图,四边形 ABCD 中,$AD// BC$,$AD = CD$,E 是对角线 BD 上一点,且$EA = EC$.
(1)求证:四边形 ABCD 是菱形;
在$\triangle ADE$与$\triangle CDE$中，$\begin{cases}AD = CD,\\DE = DE,\\EA = EC,\end{cases}$ $\therefore \triangle ADE\cong \triangle CDE$，$\therefore \angle ADE = \angle CDE$。$\because AD// BC$，$\therefore \angle ADE = \angle CBD$，$\therefore \angle CDE = \angle CBD$，$\therefore BC = CD$。$\because AD = CD$，$\therefore BC = AD$，又$AD// BC$，$\therefore$四边形$ABCD$为平行四边形。$\because AD = CD$，$\therefore □ ABCD$是菱形。
(2)如果$BE = BC$,且$∠CBE:∠BCE = 2:3$,求证:四边形 ABCD 是正方形.
$\because BE = BC$，$\therefore \angle BCE = \angle BEC$。$\because \angle CBE:\angle BCE = 2:3$，$\therefore \angle CBE = 180^{\circ}× \frac{2}{2 + 3} = 45^{\circ}$。$\because$四边形$ABCD$是菱形，$\therefore \angle ABE = 45^{\circ}$，$\therefore \angle ABC = 90^{\circ}$，$\therefore$四边形$ABCD$是正方形。

答案：
(1)在$\triangle ADE$与$\triangle CDE$中，$\begin{cases}AD = CD,\\DE = DE,\\EA = EC,\end{cases}$ $\therefore \triangle ADE\cong \triangle CDE$，$\therefore \angle ADE = \angle CDE$。$\because AD// BC$，$\therefore \angle ADE = \angle CBD$，$\therefore \angle CDE = \angle CBD$，$\therefore BC = CD$。$\because AD = CD$，$\therefore BC = AD$，又$AD// BC$，$\therefore$四边形$ABCD$为平行四边形。$\because AD = CD$，$\therefore □ ABCD$是菱形。
(2)$\because BE = BC$，$\therefore \angle BCE = \angle BEC$。$\because \angle CBE:\angle BCE = 2:3$，$\therefore \angle CBE = 180^{\circ}× \frac{2}{2 + 3} = 45^{\circ}$。$\because$四边形$ABCD$是菱形，$\therefore \angle ABE = 45^{\circ}$，$\therefore \angle ABC = 90^{\circ}$，$\therefore$四边形$ABCD$是正方形。

拳击枪
取四根同样长度的木条,可以用四根钉子将它们钉成菱形框架,在顶点处能自由转动. 从左右两侧向中间推挤,菱形变得瘦而长;向左右两旁拉开,菱形变得矮而胖.
这个简单道理,被广泛应用到活动栅栏门上. 现在很多学校、工厂和机关的大门,都采用了电控活动栅栏门,每扇门由若干全等的活动菱形组成. 电钮一按,所有菱形都往瘦长方面变化,门就开大了. 电钮再一按,所有菱形都往矮胖方向变化,门就关小了.
同样的道理还能应用到玩具上.
如图,将类似于活动栅栏门的菱形结构后端装在塑料玩具手枪的枪口上,前端连接一只塑料拳头,成为拳击枪. 玩的时候,右手握枪,食指扣动扳机,一记右直拳就打出去了. 松开扳机,塑料拳头又收了回来.

数学真奇妙!你也试着运用一个数学原理制作一个玩具吧!运用三角形的稳定性制作一个可折叠的小书架玩具。取三根木条钉成三角形框架作为书架的基本支撑结构，由于三角形具有稳定性，能稳固放置书籍，再添加可活动的连接部件实现折叠功能。

答案： 【解析】：题目主要讲述了菱形框架具有不稳定性，其形状可通过推挤或拉开改变，这一原理应用于活动栅栏门和拳击枪等。要求运用一个数学原理制作玩具，菱形的不稳定性是核心数学原理，基于此可以设计类似利用图形稳定性或不稳定性的玩具。
【答案】：运用三角形的稳定性制作一个可折叠的小书架玩具。取三根木条钉成三角形框架作为书架的基本支撑结构，由于三角形具有稳定性，能稳固放置书籍，再添加可活动的连接部件实现折叠功能。