《2025年假日时光暑假作业阳光出版社八年级数学人教版》

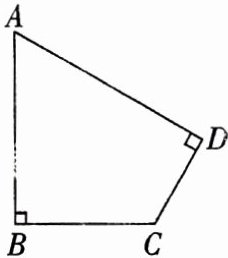
30. (5分)如图,在四边形$A B C D$中,$A B = 2$,$C D = 1$,$\angle A = 60 ^ { \circ }$,$\angle B = \angle D = 90 ^ { \circ }$,求四边形$A B C D$的面积.

$\frac{3\sqrt{3}}{2}$

答案： 【解析】：延长AD、BC交于点E。在Rt△ABE中，∠A=60°，∠B=90°，AB=2，所以∠E=30°。根据三角函数，AE=2AB=4，BE=AB·tan60°=2√3，故S_△ABE=$\frac{1}{2}$×AB×BE=$\frac{1}{2}$×2×2√3=2√3。
在Rt△CDE中，∠D=90°，∠E=30°，CD=1，所以CE=2CD=2，DE=CD·tan60°=√3，故S_△CDE=$\frac{1}{2}$×CD×DE=$\frac{1}{2}$×1×√3=$\frac{\sqrt{3}}{2}$。
四边形ABCD的面积=S_△ABE-S_△CDE=2√3 - $\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$。
【答案】：$\frac{3\sqrt{3}}{2}$

31. (5分)如图,在平行四边形$A B C D$中,$E$、$F分别在A D$、$B C$边上,且$A E = C F$,求证:四边形$B F D E$是平行四边形

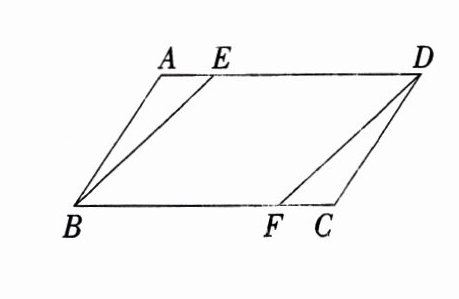
证明：因为四边形$ABCD$是平行四边形，所以$AD// BC$且$AD = BC$。又因为$AE = CF$，所以$AD - AE=BC - CF$，即$DE = BF$。由于$DE// BF$且$DE = BF$，根据一组对边平行且相等的四边形是平行四边形，可得四边形$BFDE$是平行四边形。
故答案为：四边形$BFDE$是平行四边形

答案： 【解析】：因为四边形$ABCD$是平行四边形，所以$AD// BC$且$AD = BC$。又因为$AE = CF$，所以$AD - AE=BC - CF$，即$DE = BF$。由于$DE// BF$且$DE = BF$，根据一组对边平行且相等的四边形是平行四边形，可得四边形$BFDE$是平行四边形。
【答案】：四边形$BFDE$是平行四边形。

32. (5分)如图,$B D$、$C E是\triangle A B C$的高,$G$,$F分别是B C$,$D E$的中点,求证:$F G \perp D E$.


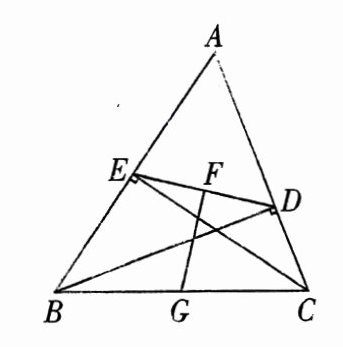
证明：连接EG、DG。
因为BD、CE是△ABC的高，所以△BEC和△BDC均为直角三角形。
由于G是BC的中点，根据直角三角形斜边中线定理，可得：
在Rt△BEC中，$EG = \frac{1}{2}BC$；在Rt△BDC中，$DG = \frac{1}{2}BC$。
因此，$EG = DG$，即△EDG是等腰三角形。
又因为F是DE的中点，根据等腰三角形三线合一的性质，所以$FG \perp DE$。

答案： 【解析】：连接EG、DG。
因为BD、CE是△ABC的高，所以△BEC和△BDC均为直角三角形。
由于G是BC的中点，根据直角三角形斜边中线定理，直角三角形斜边的中线等于斜边的一半，可得：
在Rt△BEC中，$EG = \frac{1}{2}BC$；在Rt△BDC中，$DG = \frac{1}{2}BC$。
因此，$EG = DG$，即△EDG是等腰三角形。
又因为F是DE的中点，根据等腰三角形三线合一的性质，底边上的中线垂直于底边，所以$FG \perp DE$。
【答案】：FG⊥DE