2025年假日时光暑假作业阳光出版社八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假日时光暑假作业阳光出版社八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
34. (12分)如图所示,已知直线$l过点A(0,1)和B(1,0),P是x$轴正半轴上的动点,$OP的垂直平分线交l于点Q$,交$x轴于点M$.
(1)直接写出直线$l$的解析式.
(2)设$OP = t,\triangle OPQ的面积为S$,求$S关于t$的函数关系式;并求出当$0 < t < 2$时,$S$的最大值.
(3)直线$l_1过点A且与x$轴平行,问在$l_1上是否存在点C$,使得$\triangle CPQ是以Q$为直角顶点的等腰直角三角形? 若存在,求出点$C$的坐标,并证明;若不存在,请说明理由.
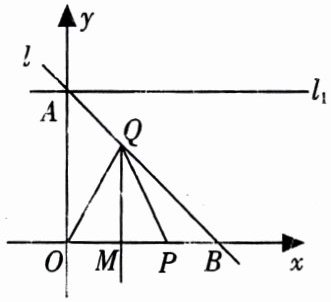
(1)直接写出直线$l$的解析式.
(2)设$OP = t,\triangle OPQ的面积为S$,求$S关于t$的函数关系式;并求出当$0 < t < 2$时,$S$的最大值.
(3)直线$l_1过点A且与x$轴平行,问在$l_1上是否存在点C$,使得$\triangle CPQ是以Q$为直角顶点的等腰直角三角形? 若存在,求出点$C$的坐标,并证明;若不存在,请说明理由.

答案:
(1)$y=1-x$.
(2)$\because OP=t,\therefore Q$点的横坐标为$\frac{1}{2}t$,
①当$0<\frac{1}{2}t<1$,即$0<t<2$时,$QM=1-\frac{1}{2}t,\therefore S_{△OPQ}=\frac{1}{2}t(1-\frac{1}{2}t)$.
②当$t≥2$时,$QM=|1-\frac{1}{2}t|=\frac{1}{2}t-1,\therefore S_{△OPQ}=\frac{1}{2}t(\frac{1}{2}t-1)$.
$\therefore S=\left\{\begin{array}{l} \frac{1}{2}t(1-\frac{1}{2}t),0<t<2,\\ \frac{1}{2}t(\frac{1}{2}t-1),t≥2.\end{array}\right.$
当$0<\frac{1}{2}t<1$,即$0<t<2$时,$S=\frac{1}{2}t(1-\frac{1}{2}t)=-\frac{1}{4}(t-1)^{2}+\frac{1}{4}$,
$\therefore$ 当$t=1$时,S有最大值$\frac{1}{4}$.
(3)由$OA=OB=1$,得$△OAB$是等腰直角三角形.若在$l_{1}$上存在点 C,使得$△CPQ$是以 Q 为直角顶点的等腰直角三角形,则$PQ=QC,\therefore OQ=QC$,又$l_{1}// x$轴,则 C,O 两点关于直线 l 对称,
$\therefore AC=OA=1$,得$C(1,1)$.下面证$∠PQC=90^{\circ }$.连接 CB,则四边形 OACB 是正方形.
①当点 P 在线段 OB 上,Q 在线段 AB 上(Q 与 B、C 不重合)时,如图-1.由对称性,得$∠BCQ=∠QOP,∠QPO=∠QOP$,
$\therefore ∠QPB+∠QCB=∠QPB+∠QPO=180^{\circ }$,
$\therefore ∠PQC=360^{\circ }-(∠QPB+∠QCB+∠PBC)$
$=90^{\circ }$.
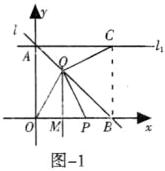
②当点 P 在线段 OB 的延长线上,Q 在线段 AB 上时,如图-2,如图-3.


$\because ∠QPB=∠QCB,∠1=∠2,\therefore ∠PQC=∠PBC=90^{\circ }$.
③当点 Q 与点 B 重合时,显然$∠PQC=90^{\circ }$.
综合①②③,$∠PQC=90^{\circ }$.
$\therefore$ 在$l_{1}$上存在点$C(1,1)$,使得$△CPQ$是以 Q 为直角顶点的等腰直角三角形.
(1)$y=1-x$.
(2)$\because OP=t,\therefore Q$点的横坐标为$\frac{1}{2}t$,
①当$0<\frac{1}{2}t<1$,即$0<t<2$时,$QM=1-\frac{1}{2}t,\therefore S_{△OPQ}=\frac{1}{2}t(1-\frac{1}{2}t)$.
②当$t≥2$时,$QM=|1-\frac{1}{2}t|=\frac{1}{2}t-1,\therefore S_{△OPQ}=\frac{1}{2}t(\frac{1}{2}t-1)$.
$\therefore S=\left\{\begin{array}{l} \frac{1}{2}t(1-\frac{1}{2}t),0<t<2,\\ \frac{1}{2}t(\frac{1}{2}t-1),t≥2.\end{array}\right.$
当$0<\frac{1}{2}t<1$,即$0<t<2$时,$S=\frac{1}{2}t(1-\frac{1}{2}t)=-\frac{1}{4}(t-1)^{2}+\frac{1}{4}$,
$\therefore$ 当$t=1$时,S有最大值$\frac{1}{4}$.
(3)由$OA=OB=1$,得$△OAB$是等腰直角三角形.若在$l_{1}$上存在点 C,使得$△CPQ$是以 Q 为直角顶点的等腰直角三角形,则$PQ=QC,\therefore OQ=QC$,又$l_{1}// x$轴,则 C,O 两点关于直线 l 对称,
$\therefore AC=OA=1$,得$C(1,1)$.下面证$∠PQC=90^{\circ }$.连接 CB,则四边形 OACB 是正方形.
①当点 P 在线段 OB 上,Q 在线段 AB 上(Q 与 B、C 不重合)时,如图-1.由对称性,得$∠BCQ=∠QOP,∠QPO=∠QOP$,
$\therefore ∠QPB+∠QCB=∠QPB+∠QPO=180^{\circ }$,
$\therefore ∠PQC=360^{\circ }-(∠QPB+∠QCB+∠PBC)$
$=90^{\circ }$.

②当点 P 在线段 OB 的延长线上,Q 在线段 AB 上时,如图-2,如图-3.


$\because ∠QPB=∠QCB,∠1=∠2,\therefore ∠PQC=∠PBC=90^{\circ }$.
③当点 Q 与点 B 重合时,显然$∠PQC=90^{\circ }$.
综合①②③,$∠PQC=90^{\circ }$.
$\therefore$ 在$l_{1}$上存在点$C(1,1)$,使得$△CPQ$是以 Q 为直角顶点的等腰直角三角形.
查看更多完整答案,请扫码查看


