1. 计算$(2a^{2})^{3}$的结果是 (
A.$2a^{6}$;
B.$8a^{6}$;
C.$8a^{5}$;
D.$8a^{8}$.
B
)A.$2a^{6}$;
B.$8a^{6}$;
C.$8a^{5}$;
D.$8a^{8}$.
答案:
【解析】:
本题主要考查幂的乘方与积的乘方的运算。
根据幂的乘方运算法则,$(a^m)^n = a^{m × n}$,以及积的乘方运算法则,$(ab)^n = a^n × b^n$,我们可以计算$(2a^{2})^{3}$。
首先,将2和$a^2$分别进行三次方运算,即$2^3 = 8$,$(a^2)^3 = a^{2 × 3} = a^6$。
然后,将这两个结果相乘,得到$8 × a^6 = 8a^6$。
【答案】:
B
本题主要考查幂的乘方与积的乘方的运算。
根据幂的乘方运算法则,$(a^m)^n = a^{m × n}$,以及积的乘方运算法则,$(ab)^n = a^n × b^n$,我们可以计算$(2a^{2})^{3}$。
首先,将2和$a^2$分别进行三次方运算,即$2^3 = 8$,$(a^2)^3 = a^{2 × 3} = a^6$。
然后,将这两个结果相乘,得到$8 × a^6 = 8a^6$。
【答案】:
B
2. 对于$(-3)^{3}与-3^{3}$,下列叙述正确的是 (
A.底数相同,运算结果相同;
B.底数相同,运算结果不相同;
C.底数不同,运算结果相同;
D.底数不同,运算结果不相同.
C
)A.底数相同,运算结果相同;
B.底数相同,运算结果不相同;
C.底数不同,运算结果相同;
D.底数不同,运算结果不相同.
答案:
解:对于$(-3)^3$,底数是$-3$,运算结果为$(-3)×(-3)×(-3)=-27$;对于$-3^3$,底数是$3$,运算结果为$-(3×3×3)=-27$。所以底数不同,运算结果相同。
答案:C
答案:C
3. 下列多项式中,能用完全平方公式计算的是 (
A.$(a+1)(-a+1)$;
B.$(a+b)(b-a)$;
C.$(-a+b)(a-b)$;
D.$(a-b)(a+b)$.
C
)A.$(a+1)(-a+1)$;
B.$(a+b)(b-a)$;
C.$(-a+b)(a-b)$;
D.$(a-b)(a+b)$.
答案:
解:完全平方公式为$(m\pm n)^2 = m^2 \pm 2mn + n^2$,其特点是两个相同的二项式相乘。
A. $(a + 1)(-a + 1) = (1 + a)(1 - a) = 1 - a^2$,为平方差公式,不符合。
B. $(a + b)(b - a) = (b + a)(b - a) = b^2 - a^2$,为平方差公式,不符合。
C. $(-a + b)(a - b) = -(a - b)(a - b) = -(a - b)^2$,符合完全平方公式形式。
D. $(a - b)(a + b) = a^2 - b^2$,为平方差公式,不符合。
答案:C
A. $(a + 1)(-a + 1) = (1 + a)(1 - a) = 1 - a^2$,为平方差公式,不符合。
B. $(a + b)(b - a) = (b + a)(b - a) = b^2 - a^2$,为平方差公式,不符合。
C. $(-a + b)(a - b) = -(a - b)(a - b) = -(a - b)^2$,符合完全平方公式形式。
D. $(a - b)(a + b) = a^2 - b^2$,为平方差公式,不符合。
答案:C
4. 如果$a^{2}-(b-c)^{2}$有一个因式是$a+b-c$,那么它的另一个因式是 (
A.$a-b-c$;
B.$a-b+c$;
C.$a+b-c$;
D.$a+b+c$.
B
)A.$a-b-c$;
B.$a-b+c$;
C.$a+b-c$;
D.$a+b+c$.
答案:
【解析】:
本题主要考察平方差公式的应用。
首先,根据平方差公式,可以将$a^{2} - (b - c)^{2}$进行因式分解。
平方差公式为:$A^{2} - B^{2} = (A + B)(A - B)$。
应用此公式,得到:
$a^{2} - (b - c)^{2} = (a + (b - c))(a - (b - c))$
$= (a + b - c)(a - b + c)$
题目已给出一个因式是$a + b - c$,通过比较,可以发现另一个因式是$a - b + c$。
【答案】:B
本题主要考察平方差公式的应用。
首先,根据平方差公式,可以将$a^{2} - (b - c)^{2}$进行因式分解。
平方差公式为:$A^{2} - B^{2} = (A + B)(A - B)$。
应用此公式,得到:
$a^{2} - (b - c)^{2} = (a + (b - c))(a - (b - c))$
$= (a + b - c)(a - b + c)$
题目已给出一个因式是$a + b - c$,通过比较,可以发现另一个因式是$a - b + c$。
【答案】:B
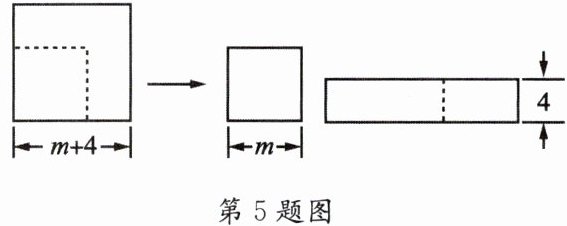
5. 如图,边长为$m+4的正方形纸片剪出一个边长为m$的正方形之后,剩余部分可剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为4,则另一边长是 (
A.$m+4$;
B.$m+8$;
C.$2m+4$;
D.$2m+8$.
C
)
A.$m+4$;
B.$m+8$;
C.$2m+4$;
D.$2m+8$.
答案:
【解析】:
首先,计算大正方形的面积。
大正方形的边长为$m+4$,所以面积为:
$S_{\text{大正方形}} = (m+4)^2 = m^2 + 8m + 16$,
接着,计算小正方形的面积。
小正方形的边长为$m$,所以面积为:
$S_{\text{小正方形}} = m^2$,
然后,计算剩余部分的面积。
剩余部分的面积是大正方形面积减去小正方形面积:
$S_{\text{剩余}} = S_{\text{大正方形}} - S_{\text{小正方形}} = (m^2 + 8m + 16) - m^2 = 8m + 16$,
题目中说剩余部分可以剪拼成一个矩形,且这个矩形的一边长为4。
设另一边长为$x$,则矩形的面积为:
$S_{\text{矩形}} = 4 × x$,
由于剩余部分的面积等于矩形的面积,所以有:
$4x = 8m + 16$,
解这个方程,得到:
$x = \frac{8m + 16}{4} = 2m + 4$。
【答案】:C. $2m+4$。
首先,计算大正方形的面积。
大正方形的边长为$m+4$,所以面积为:
$S_{\text{大正方形}} = (m+4)^2 = m^2 + 8m + 16$,
接着,计算小正方形的面积。
小正方形的边长为$m$,所以面积为:
$S_{\text{小正方形}} = m^2$,
然后,计算剩余部分的面积。
剩余部分的面积是大正方形面积减去小正方形面积:
$S_{\text{剩余}} = S_{\text{大正方形}} - S_{\text{小正方形}} = (m^2 + 8m + 16) - m^2 = 8m + 16$,
题目中说剩余部分可以剪拼成一个矩形,且这个矩形的一边长为4。
设另一边长为$x$,则矩形的面积为:
$S_{\text{矩形}} = 4 × x$,
由于剩余部分的面积等于矩形的面积,所以有:
$4x = 8m + 16$,
解这个方程,得到:
$x = \frac{8m + 16}{4} = 2m + 4$。
【答案】:C. $2m+4$。
6. 多项式$2x^{2}y+3xy-1$的次数是
三
次,常数项是$-1$
,二次项的系数是$3$
.
答案:
【解析】:
本题主要考察多项式的次数,常数项以及二次项系数的定义。
多项式的次数是指多项式中单项式的最高次数。
常数项是多项式中不含变量的项。
二次项则是多项式中变量次数和为2的单项式。
首先,观察多项式$2x^{2}y + 3xy - 1$,
对于$2x^{2}y$,它的次数是$2+1=3$($x$的次数为2,$y$的次数为1),
对于$3xy$,它的次数是$1+1=2$,
对于$-1$,它是常数项,次数为0,
所以,多项式$2x^{2}y + 3xy - 1$中,最高次数的单项式是$2x^{2}y$,次数为3,
常数项是$-1$,
二次项是$3xy$,其系数是$3$,
【答案】:
三;$- 1$;$3$。
本题主要考察多项式的次数,常数项以及二次项系数的定义。
多项式的次数是指多项式中单项式的最高次数。
常数项是多项式中不含变量的项。
二次项则是多项式中变量次数和为2的单项式。
首先,观察多项式$2x^{2}y + 3xy - 1$,
对于$2x^{2}y$,它的次数是$2+1=3$($x$的次数为2,$y$的次数为1),
对于$3xy$,它的次数是$1+1=2$,
对于$-1$,它是常数项,次数为0,
所以,多项式$2x^{2}y + 3xy - 1$中,最高次数的单项式是$2x^{2}y$,次数为3,
常数项是$-1$,
二次项是$3xy$,其系数是$3$,
【答案】:
三;$- 1$;$3$。
7. 合并同类项:$-6ab+ba+8ab= $
$3ab$
.
答案:
【解析】:
本题主要考查合并同类项的知识点。
在代数式中,同类项是指次数、字母均相同的项。
如本题中,$-6ab$、$ba$ 和 $8ab$ 都是关于 $a$ 和 $b$ 的一次项,
因此它们是同类项。
合并同类项的基本方法是先找出所有同类项,然后将它们的系数相加或相减,最后写出合并后的结果。
【答案】:
原式$= (-6 + 1 + 8)ab$
$= 3ab$。
本题主要考查合并同类项的知识点。
在代数式中,同类项是指次数、字母均相同的项。
如本题中,$-6ab$、$ba$ 和 $8ab$ 都是关于 $a$ 和 $b$ 的一次项,
因此它们是同类项。
合并同类项的基本方法是先找出所有同类项,然后将它们的系数相加或相减,最后写出合并后的结果。
【答案】:
原式$= (-6 + 1 + 8)ab$
$= 3ab$。
8. 如果二次三项式$x^{2}+5x+m$是一个完全平方式,那么$m= $
$\frac{25}{4}$
.
答案:
【解析】:
本题主要考察完全平方公式的应用。
完全平方公式的一般形式为$(a+b)^2 = a^2 + 2ab + b^2$。
对于给定的二次三项式$x^2 + 5x + m$,可以观察到它类似于完全平方公式的形式,其中$a=x$,$2ab=5x$。
由此可以求出$b$的值,即$2xb=5x$,解得$b=\frac{5}{2}$。
然后,可以将$b$的值代入完全平方公式的$b^2$部分,得到$m = \left(\frac{5}{2}\right)^2 = \frac{25}{4}$。
【答案】:
$m = \frac{25}{4}$
本题主要考察完全平方公式的应用。
完全平方公式的一般形式为$(a+b)^2 = a^2 + 2ab + b^2$。
对于给定的二次三项式$x^2 + 5x + m$,可以观察到它类似于完全平方公式的形式,其中$a=x$,$2ab=5x$。
由此可以求出$b$的值,即$2xb=5x$,解得$b=\frac{5}{2}$。
然后,可以将$b$的值代入完全平方公式的$b^2$部分,得到$m = \left(\frac{5}{2}\right)^2 = \frac{25}{4}$。
【答案】:
$m = \frac{25}{4}$
9. 已知$x^{m}= \frac {1}{2},x^{n}= 3$,则$x^{m+2n}= $
$\frac{9}{2}$
.
答案:
【解析】:
本题主要考查同底数幂的乘法法则和幂的乘方法则。
首先,根据同底数幂的乘法法则,有$x^{m+2n} = x^{m} \cdot x^{2n}$。
然后,根据幂的乘方法则,我们可以将$x^{2n}$转化为$(x^{n})^{2}$。
所以,原式可以进一步转化为$x^{m+2n} = x^{m} \cdot (x^{n})^{2}$。
最后,将已知的$x^{m} = \frac{1}{2}$和$x^{n} = 3$代入上式,
得到$x^{m+2n} = \frac{1}{2} × 3^{2} = \frac{9}{2}$,
也可以写成$x^{m+2n} =4.5$(化为小数形式方便理解,但一般保留分数形式)。
【答案】:
$\frac{9}{2}$
本题主要考查同底数幂的乘法法则和幂的乘方法则。
首先,根据同底数幂的乘法法则,有$x^{m+2n} = x^{m} \cdot x^{2n}$。
然后,根据幂的乘方法则,我们可以将$x^{2n}$转化为$(x^{n})^{2}$。
所以,原式可以进一步转化为$x^{m+2n} = x^{m} \cdot (x^{n})^{2}$。
最后,将已知的$x^{m} = \frac{1}{2}$和$x^{n} = 3$代入上式,
得到$x^{m+2n} = \frac{1}{2} × 3^{2} = \frac{9}{2}$,
也可以写成$x^{m+2n} =4.5$(化为小数形式方便理解,但一般保留分数形式)。
【答案】:
$\frac{9}{2}$
10. 已知$x^{2}+y^{2}-2x+1= 0$,则$xy= $
0
.
答案:
【解析】:
首先我们需要将给定的方程 $x^{2}+y^{2}-2x+1= 0$ 进行整理,通过完全平方公式将其转化为一个圆的方程或者通过配方得到更简单的形式。
通过配方,我们可以将方程 $x^{2}+y^{2}-2x+1= 0$ 改写为 $(x-1)^{2}+y^{2}=0$。
由于平方项总是非负的,所以 $(x-1)^{2}$ 和 $y^{2}$ 都必须等于0,才能使整个方程成立。
因此,我们得出 $x-1=0$ 和 $y=0$,解得 $x=1$,$y=0$。
最后,我们计算 $xy$ 的值,即 $xy=1 × 0=0$。
【答案】:
$0$
首先我们需要将给定的方程 $x^{2}+y^{2}-2x+1= 0$ 进行整理,通过完全平方公式将其转化为一个圆的方程或者通过配方得到更简单的形式。
通过配方,我们可以将方程 $x^{2}+y^{2}-2x+1= 0$ 改写为 $(x-1)^{2}+y^{2}=0$。
由于平方项总是非负的,所以 $(x-1)^{2}$ 和 $y^{2}$ 都必须等于0,才能使整个方程成立。
因此,我们得出 $x-1=0$ 和 $y=0$,解得 $x=1$,$y=0$。
最后,我们计算 $xy$ 的值,即 $xy=1 × 0=0$。
【答案】:
$0$
11. 计算:$(-x^{3})^{2}(-x^{2})^{3}+(-x^{3})^{4}$.
答案:
解:$(-x^{3})^{2}(-x^{2})^{3}+(-x^{3})^{4}$
$=x^{6}\cdot (-x^{6})+x^{12}$
$=-x^{12}+x^{12}$
$=0$
$=x^{6}\cdot (-x^{6})+x^{12}$
$=-x^{12}+x^{12}$
$=0$
12. 若$3x^{m+2n}y^{8}与-2x^{2}y^{3m+4n}$是同类项,试求$m-n$的值.
答案:
解:因为$3x^{m+2n}y^{8}$与$-2x^{2}y^{3m+4n}$是同类项,所以可得方程组:
$\begin{cases}m + 2n = 2 \\3m + 4n = 8\end{cases}$
由第一个方程得:$m = 2 - 2n$,将其代入第二个方程:
$3(2 - 2n) + 4n = 8$
$6 - 6n + 4n = 8$
$-2n = 2$
解得$n = -1$,将$n = -1$代入$m = 2 - 2n$,得$m = 2 - 2×(-1) = 4$,所以$m - n = 4 - (-1) = 5$。
答案:5
$\begin{cases}m + 2n = 2 \\3m + 4n = 8\end{cases}$
由第一个方程得:$m = 2 - 2n$,将其代入第二个方程:
$3(2 - 2n) + 4n = 8$
$6 - 6n + 4n = 8$
$-2n = 2$
解得$n = -1$,将$n = -1$代入$m = 2 - 2n$,得$m = 2 - 2×(-1) = 4$,所以$m - n = 4 - (-1) = 5$。
答案:5
查看更多完整答案,请扫码查看


