1. 下列计算正确的是 (
A.$a^{2}\cdot a^{3}= a^{6}$;
B.$(a^{3})^{2}= a^{5}$;
C.$(ab)^{2}= ab^{2}$;
D.$a^{3}÷a= a^{2}$.
D
)A.$a^{2}\cdot a^{3}= a^{6}$;
B.$(a^{3})^{2}= a^{5}$;
C.$(ab)^{2}= ab^{2}$;
D.$a^{3}÷a= a^{2}$.
答案:
【解析】:
本题主要考查幂的运算法则,包括同底数幂的乘法、幂的乘方、积的乘方以及同底数幂的除法。
A. 根据同底数幂的乘法法则,有 $a^{m} \cdot a^{n} = a^{m+n}$。
所以 $a^{2} \cdot a^{3} = a^{2+3} = a^{5}$,与选项A中的 $a^{6}$ 不符,故A错误。
B. 根据幂的乘方法则,有 $(a^{m})^{n} = a^{m × n}$。
所以 $(a^{3})^{2} = a^{3 × 2} = a^{6}$,与选项B中的 $a^{5}$ 不符,故B错误。
C. 根据积的乘方法则,有 $(ab)^{n} = a^{n}b^{n}$。
所以 $(ab)^{2} = a^{2}b^{2}$,与选项C中的 $ab^{2}$ 不符,故C错误。
D. 根据同底数幂的除法法则,有 $a^{m} ÷ a^{n} = a^{m-n}$。
所以 $a^{3} ÷ a = a^{3-1} = a^{2}$,与选项D中的 $a^{2}$ 符合,故D正确。
【答案】:
D
本题主要考查幂的运算法则,包括同底数幂的乘法、幂的乘方、积的乘方以及同底数幂的除法。
A. 根据同底数幂的乘法法则,有 $a^{m} \cdot a^{n} = a^{m+n}$。
所以 $a^{2} \cdot a^{3} = a^{2+3} = a^{5}$,与选项A中的 $a^{6}$ 不符,故A错误。
B. 根据幂的乘方法则,有 $(a^{m})^{n} = a^{m × n}$。
所以 $(a^{3})^{2} = a^{3 × 2} = a^{6}$,与选项B中的 $a^{5}$ 不符,故B错误。
C. 根据积的乘方法则,有 $(ab)^{n} = a^{n}b^{n}$。
所以 $(ab)^{2} = a^{2}b^{2}$,与选项C中的 $ab^{2}$ 不符,故C错误。
D. 根据同底数幂的除法法则,有 $a^{m} ÷ a^{n} = a^{m-n}$。
所以 $a^{3} ÷ a = a^{3-1} = a^{2}$,与选项D中的 $a^{2}$ 符合,故D正确。
【答案】:
D
2. 已知$28a^{3}b^{m}÷(28a^{n}b^{2})= b^{2}$,则$m$,$n$的值分别为 (
A.4,3;
B.4,1;
C.1,3;
D.2,3.
A
)A.4,3;
B.4,1;
C.1,3;
D.2,3.
答案:
【解析】:
本题主要考查单项式除以单项式的法则,以及指数运算的性质。
根据单项式除以单项式的法则,将给定的式子进行化简。
原式$28a^{3}b^{m} ÷ (28a^{n}b^{2})$可以化简为:
$\frac{28a^{3}b^{m}}{28a^{n}b^{2}} = a^{3-n}b^{m-2}$
由于题目给出$a^{3-n}b^{m-2} = b^{2}$,
根据指数运算的性质,当两个幂相等时,它们的底数和指数必须分别相等。
因此,可以得到以下两个方程:
$3 - n = 0$ (因为$a$的指数在等式两边必须相等,且$a$不为0,所以$a$的指数必须为0,使得$a$的项为1,不影响等式)
$m - 2 = 2$ (因为$b$的指数在等式两边必须相等)
解这两个方程,得到:
$n = 3$
$m = 4$
【答案】:
A. $4,3$。
本题主要考查单项式除以单项式的法则,以及指数运算的性质。
根据单项式除以单项式的法则,将给定的式子进行化简。
原式$28a^{3}b^{m} ÷ (28a^{n}b^{2})$可以化简为:
$\frac{28a^{3}b^{m}}{28a^{n}b^{2}} = a^{3-n}b^{m-2}$
由于题目给出$a^{3-n}b^{m-2} = b^{2}$,
根据指数运算的性质,当两个幂相等时,它们的底数和指数必须分别相等。
因此,可以得到以下两个方程:
$3 - n = 0$ (因为$a$的指数在等式两边必须相等,且$a$不为0,所以$a$的指数必须为0,使得$a$的项为1,不影响等式)
$m - 2 = 2$ (因为$b$的指数在等式两边必须相等)
解这两个方程,得到:
$n = 3$
$m = 4$
【答案】:
A. $4,3$。
3. 已知$x+2y= 6$,$xy= 3$,则$(x-2y)^{2}$等于 (
A.8;
B.12;
C.24;
D.25.
B
)A.8;
B.12;
C.24;
D.25.
答案:
【解析】:
本题主要考查完全平方公式的运用以及代数式的代入计算。
首先,我们需要将$(x-2y)^{2}$进行展开,利用完全平方公式,得到:
$(x-2y)^{2} = x^{2} - 4xy + 4y^{2}$
接着,我们注意到$x^{2} + 4y^{2}$可以表示为$(x+2y)^{2} - 4xy$,即:
$x^{2} + 4y^{2} = (x+2y)^{2} - 4xy$
代入题目给出的条件$x+2y=6$和$xy=3$,我们得到:
$(x-2y)^{2} = (x+2y)^{2} - 4xy - 4xy = 6^{2} - 8 × 3 = 36 - 24 = 12$
【答案】:
B. $12$。
本题主要考查完全平方公式的运用以及代数式的代入计算。
首先,我们需要将$(x-2y)^{2}$进行展开,利用完全平方公式,得到:
$(x-2y)^{2} = x^{2} - 4xy + 4y^{2}$
接着,我们注意到$x^{2} + 4y^{2}$可以表示为$(x+2y)^{2} - 4xy$,即:
$x^{2} + 4y^{2} = (x+2y)^{2} - 4xy$
代入题目给出的条件$x+2y=6$和$xy=3$,我们得到:
$(x-2y)^{2} = (x+2y)^{2} - 4xy - 4xy = 6^{2} - 8 × 3 = 36 - 24 = 12$
【答案】:
B. $12$。
4. 若$a^{m}= 2$,$a^{n}= 3$,$a^{p}= 5$,则$a^{2m+n-p}$的值是 (
A.2.4;
B.2;
C.1;
D.0.
A
)A.2.4;
B.2;
C.1;
D.0.
答案:
【解析】:
本题主要考查同底数幂的乘法与除法法则及幂的乘方与积的乘方法则。
根据同底数幂的乘法法则:$a^{m+n} = a^m × a^n$,
及同底数幂的除法法则:$a^{m-n} = \frac{a^m}{a^n}$,
我们可以将$a^{2m+n-p}$拆分为$a^{2m} × a^{n} ÷ a^{p}$,
再根据幂的乘方法则:$(a^m)^n = a^{mn}$,
我们可以进一步化简$a^{2m}$为$(a^{m})^2$,
代入题目给定的$a^{m}= 2$,$a^{n}= 3$,$a^{p}= 5$,
我们得到:
$a^{2m+n-p} = (a^{m})^2 × a^{n} ÷ a^{p} = 2^2 × 3 ÷ 5 = \frac{12}{5} = 2.4$。
【答案】:A. $2.4$。
本题主要考查同底数幂的乘法与除法法则及幂的乘方与积的乘方法则。
根据同底数幂的乘法法则:$a^{m+n} = a^m × a^n$,
及同底数幂的除法法则:$a^{m-n} = \frac{a^m}{a^n}$,
我们可以将$a^{2m+n-p}$拆分为$a^{2m} × a^{n} ÷ a^{p}$,
再根据幂的乘方法则:$(a^m)^n = a^{mn}$,
我们可以进一步化简$a^{2m}$为$(a^{m})^2$,
代入题目给定的$a^{m}= 2$,$a^{n}= 3$,$a^{p}= 5$,
我们得到:
$a^{2m+n-p} = (a^{m})^2 × a^{n} ÷ a^{p} = 2^2 × 3 ÷ 5 = \frac{12}{5} = 2.4$。
【答案】:A. $2.4$。
5. 如图,从边长为$(a+1)\mathrm{cm}$的正方形纸片中剪去一个边长为$(a-1)\mathrm{cm}$的正方形$(a>1)$,剩余部分沿虚线又剪拼成一个长方形(不重叠、无缝隙),则该长方形的面积是 (
A.2平方厘米;
B.$2a$平方厘米;
C.$4a$平方厘米;
D.$(a^{2}-1)$平方厘米.
C
)A.2平方厘米;
B.$2a$平方厘米;
C.$4a$平方厘米;
D.$(a^{2}-1)$平方厘米.
答案:
【解析】:本题考查的知识点是平方差公式和面积的计算。
原图是一个边长为$(a+1)cm$的正方形,中间挖去了一个边长为$(a-1)cm$的小正方形。
剩余部分的面积即为大正方形的面积减去小正方形的面积。
大正方形的面积:$(a+1)^2$,
小正方形的面积:$(a-1)^2$,
剩余部分的面积:$(a+1)^2-(a-1)^2$,
利用平方差公式:$A^2-B^2=(A+B)(A-B)$,
这里,$A=(a+1)$,$B=(a-1)$,
所以,$(a+1)^2-(a-1)^2=[(a+1)+(a-1)][(a+1)-(a-1)]$,
化简得:$(2a)(2)=4a(平方厘米)$,
则剩余部分剪拼成的矩形的面积为$4a$平方厘米。
【答案】:C。
原图是一个边长为$(a+1)cm$的正方形,中间挖去了一个边长为$(a-1)cm$的小正方形。
剩余部分的面积即为大正方形的面积减去小正方形的面积。
大正方形的面积:$(a+1)^2$,
小正方形的面积:$(a-1)^2$,
剩余部分的面积:$(a+1)^2-(a-1)^2$,
利用平方差公式:$A^2-B^2=(A+B)(A-B)$,
这里,$A=(a+1)$,$B=(a-1)$,
所以,$(a+1)^2-(a-1)^2=[(a+1)+(a-1)][(a+1)-(a-1)]$,
化简得:$(2a)(2)=4a(平方厘米)$,
则剩余部分剪拼成的矩形的面积为$4a$平方厘米。
【答案】:C。
6. 如图,有两张正方形纸片$A和B$,图①将$B放置在A$内部,测得阴影部分面积为2;图②将正方形$A和正方形B$并列放置后构造新正方形,测得阴影部分面积为6.若将3个正方形$A$和2个正方形$B$并列放置后构造新正方形如图③(图②、图③中正方形$A$,$B$纸片均无重叠部分),则图③阴影部分面积为 (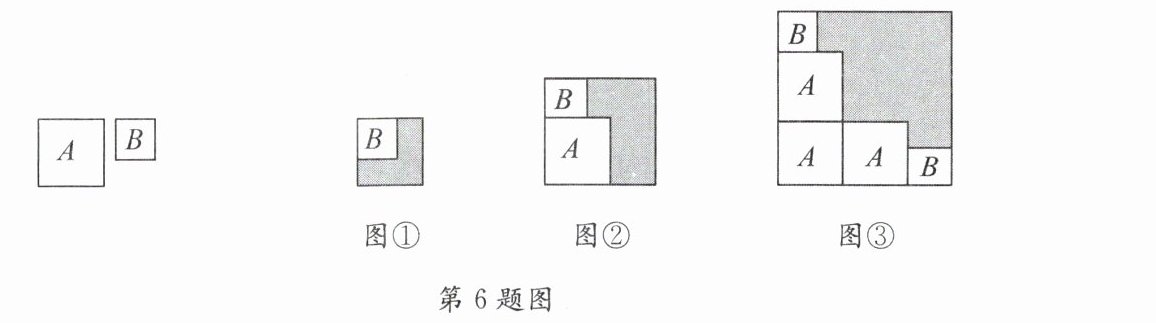
A.14;
B.12;
C.24;
D.22.
A
)
A.14;
B.12;
C.24;
D.22.
答案:
A
7. 计算:$(-a-b)^{5}\cdot (a+b)^{3}= $
$-(a+b)^8$
.
答案:
【解析】:
本题主要考查同底数幂的乘法法则和整体代入的思想。
首先,我们可以将$(-a-b)^{5}$看作$-1$乘以$(a+b)$的五次方,即$(-a-b)^{5} = - (a+b)^{5}$。
接着,我们利用同底数幂的乘法法则,即$a^{m} \cdot a^{n} = a^{m+n}$,将$(a+b)^{5}$与$(a+b)^{3}$相乘,得到$(a+b)^{5+3} = (a+b)^{8}$。
最后,将上述结果乘以$-1$,得到$- (a+b)^{8}$。
【答案】:
$- (a + b)^{8}$
本题主要考查同底数幂的乘法法则和整体代入的思想。
首先,我们可以将$(-a-b)^{5}$看作$-1$乘以$(a+b)$的五次方,即$(-a-b)^{5} = - (a+b)^{5}$。
接着,我们利用同底数幂的乘法法则,即$a^{m} \cdot a^{n} = a^{m+n}$,将$(a+b)^{5}$与$(a+b)^{3}$相乘,得到$(a+b)^{5+3} = (a+b)^{8}$。
最后,将上述结果乘以$-1$,得到$- (a+b)^{8}$。
【答案】:
$- (a + b)^{8}$
8. 若$x^{3m}= 2$,则$x^{9m}= $
8
.
答案:
【解析】:
本题主要考察幂的乘方运算法则。根据幂的乘方公式$(a^m)^n = a^{mn}$,我们可以将$x^{9m}$拆分为$(x^{3m})^3$。
已知$x^{3m} = 2$,所以可以将$x^{3m}$的值代入$(x^{3m})^3$中,得到$2^3 = 8$。
【答案】:
$x^{9m} = 8$。
本题主要考察幂的乘方运算法则。根据幂的乘方公式$(a^m)^n = a^{mn}$,我们可以将$x^{9m}$拆分为$(x^{3m})^3$。
已知$x^{3m} = 2$,所以可以将$x^{3m}$的值代入$(x^{3m})^3$中,得到$2^3 = 8$。
【答案】:
$x^{9m} = 8$。
9. 计算:$(-2ab)\cdot 5ab^{3}\cdot (-\frac{3}{5}a^{2}b^{2})=$
$6a^{4}b^{6}$
.
答案:
【解析】:
本题考查了单项式乘单项式的运算法则,即系数与系数相乘,字母部分按照同底数幂的乘法法则进行计算。
首先,我们计算系数部分:
$(-2) × 5 × (-\frac{3}{5}) = 6 × (-\frac{1}{1}×\frac{5}{1}×\frac{3}{5}) = 6 × (-1) × \frac{3}{1} ×\frac{5}{5}= 6$
接着,我们计算字母部分:
对于a的幂次,我们有:
$a \cdot a \cdot a^{2} = a^{1+1+2} = a^{4}$
对于b的幂次,我们有:
$b \cdot b^{3} \cdot b^{2} = b^{1+3+2} = b^{6}$
因此,原式可以表示为:
$6a^{4}b^{6}$
【答案】:
$6a^{4}b^{6}$
本题考查了单项式乘单项式的运算法则,即系数与系数相乘,字母部分按照同底数幂的乘法法则进行计算。
首先,我们计算系数部分:
$(-2) × 5 × (-\frac{3}{5}) = 6 × (-\frac{1}{1}×\frac{5}{1}×\frac{3}{5}) = 6 × (-1) × \frac{3}{1} ×\frac{5}{5}= 6$
接着,我们计算字母部分:
对于a的幂次,我们有:
$a \cdot a \cdot a^{2} = a^{1+1+2} = a^{4}$
对于b的幂次,我们有:
$b \cdot b^{3} \cdot b^{2} = b^{1+3+2} = b^{6}$
因此,原式可以表示为:
$6a^{4}b^{6}$
【答案】:
$6a^{4}b^{6}$
10. 计算:$(a-b)(a+b)(a^{2}+b^{2})= $
$a^{4} - b^{4}$
.
答案:
【解析】:
本题主要考查平方差公式及代数式的乘法。题目给出了三个因子:$(a-b)$,$(a+b)$ 和 $(a^{2}+b^{2})$,需要依次进行乘法运算。首先,可以利用平方差公式将前两个因子相乘,即:$(a-b)(a+b) = a^{2} - b^{2}$。然后,再将这个结果与第三个因子相乘,即:$(a^{2} - b^{2})(a^{2} + b^{2}) = a^{4} - b^{4}$。
【答案】:
$a^{4} - b^{4}$
本题主要考查平方差公式及代数式的乘法。题目给出了三个因子:$(a-b)$,$(a+b)$ 和 $(a^{2}+b^{2})$,需要依次进行乘法运算。首先,可以利用平方差公式将前两个因子相乘,即:$(a-b)(a+b) = a^{2} - b^{2}$。然后,再将这个结果与第三个因子相乘,即:$(a^{2} - b^{2})(a^{2} + b^{2}) = a^{4} - b^{4}$。
【答案】:
$a^{4} - b^{4}$
11. 计算:$(a-1)^{2}-a(a-2)= $
1
.
答案:
【解析】:
本题主要考查完全平方公式和单项式乘多项式的运算。
首先,我们展开$(a-1)^{2}$,根据完全平方公式,有
$(a-1)^{2} = a^{2} - 2a + 1$
接着,我们展开$a(a-2)$,根据单项式乘多项式的法则,有
$a(a-2) = a^{2} - 2a$
现在,我们将两个展开后的式子进行相减:
$(a^{2} - 2a + 1) - (a^{2} - 2a) = 1$
【答案】:
1
本题主要考查完全平方公式和单项式乘多项式的运算。
首先,我们展开$(a-1)^{2}$,根据完全平方公式,有
$(a-1)^{2} = a^{2} - 2a + 1$
接着,我们展开$a(a-2)$,根据单项式乘多项式的法则,有
$a(a-2) = a^{2} - 2a$
现在,我们将两个展开后的式子进行相减:
$(a^{2} - 2a + 1) - (a^{2} - 2a) = 1$
【答案】:
1
12. 计算:$(x^{8}÷x^{2})^{3}÷(x^{4})^{3}\cdot x^{6}= $
$x^{12}$
.
答案:
【解析】:
本题主要考查幂的乘方、同底数幂的除法和乘法法则。
首先,我们根据幂的乘方法则,有 $(a^m)^n = a^{m × n}$ ,所以 $(x^{8}÷x^{2})^{3}$ 可以化简为 $(x^{6})^{3} = x^{18}$ 。
同样,$(x^{4})^{3}$ 可以化简为 $x^{12}$ 。
因此,原式可以表示为:
$x^{18} ÷ x^{12} \cdot x^{6}$
再根据同底数幂的除法法则,有 $a^m ÷ a^n = a^{m-n}$ ,所以 $x^{18} ÷ x^{12}$ 可以化简为 $x^{6}$ 。
最后,根据同底数幂的乘法法则,有 $a^m × a^n = a^{m+n}$ ,所以 $x^{6} \cdot x^{6}$ 可以化简为 $x^{12}$ 。
【答案】:
$x^{12}$
本题主要考查幂的乘方、同底数幂的除法和乘法法则。
首先,我们根据幂的乘方法则,有 $(a^m)^n = a^{m × n}$ ,所以 $(x^{8}÷x^{2})^{3}$ 可以化简为 $(x^{6})^{3} = x^{18}$ 。
同样,$(x^{4})^{3}$ 可以化简为 $x^{12}$ 。
因此,原式可以表示为:
$x^{18} ÷ x^{12} \cdot x^{6}$
再根据同底数幂的除法法则,有 $a^m ÷ a^n = a^{m-n}$ ,所以 $x^{18} ÷ x^{12}$ 可以化简为 $x^{6}$ 。
最后,根据同底数幂的乘法法则,有 $a^m × a^n = a^{m+n}$ ,所以 $x^{6} \cdot x^{6}$ 可以化简为 $x^{12}$ 。
【答案】:
$x^{12}$
查看更多完整答案,请扫码查看


