1. 计算$(1 + 3x)(3x - 1) + 9(\frac{1}{3} - x)(x + \frac{1}{3})$的结果是(
A.$18x^{2}-2$;
B.$2 - 18x^{2}$;
C.$0$;
D.$8x^{2}$.
C
)A.$18x^{2}-2$;
B.$2 - 18x^{2}$;
C.$0$;
D.$8x^{2}$.
答案:
【解析】:
本题主要考察平方差公式和乘法分配律的运用。
首先,我们分别展开两个括号内的乘积:
$(1 + 3x)(3x - 1) = 3x + 9x^{2} - 1 - 3x = 9x^{2} - 1$
$9(\frac{1}{3} - x)(x + \frac{1}{3}) = 9(\frac{1}{3}x + \frac{1}{9} - x^{2} - \frac{1}{3}x) = 9(\frac{1}{9} - x^{2}) = 1 - 9x^{2}$
将上述两个结果相加,得到:
$9x^{2} - 1 + 1 - 9x^{2} = 0$
【答案】:
C
本题主要考察平方差公式和乘法分配律的运用。
首先,我们分别展开两个括号内的乘积:
$(1 + 3x)(3x - 1) = 3x + 9x^{2} - 1 - 3x = 9x^{2} - 1$
$9(\frac{1}{3} - x)(x + \frac{1}{3}) = 9(\frac{1}{3}x + \frac{1}{9} - x^{2} - \frac{1}{3}x) = 9(\frac{1}{9} - x^{2}) = 1 - 9x^{2}$
将上述两个结果相加,得到:
$9x^{2} - 1 + 1 - 9x^{2} = 0$
【答案】:
C
2. $(-x + y)(y^{2} + x^{2})$再乘以一个多项式得$x^{4}-y^{4}$,则这个多项式是(
A.$x - y$;
B.$x + y$;
C.$-x + y$;
D.$-x - y$.
D
)A.$x - y$;
B.$x + y$;
C.$-x + y$;
D.$-x - y$.
答案:
【解析】:
本题主要考察平方差公式$a^2 - b^2 = (a + b)(a - b)$的应用以及多项式乘法。
首先,我们观察目标表达式$x^{4} - y^{4}$,它可以看作是$(x^{2})^{2} - (y^{2})^{2}$,即平方差的形式。
根据平方差公式,我们可以将其分解为:
$x^{4} - y^{4} = (x^{2} + y^{2})(x^{2} - y^{2})$
接着,我们注意到$x^{2} - y^{2}$还可以继续分解为$(x + y)(x - y)$,所以:
$x^{4} - y^{4} = (x^{2} + y^{2})(x + y)(x - y)$
题目中已经给出了$(-x + y)(y^{2} + x^{2})$,我们需要找到一个多项式,使得它与这个表达式相乘得到$x^{4} - y^{4}$。
对比上述两个表达式,我们可以发现这个多项式应该是$-(x + y)$,即$-x - y$,因为:
$(-x + y)(y^{2} + x^{2})(-x - y) = (x^{2} + y^{2})(x + y)(x - y) × (-1) × (-1) = (x^{2} + y^{2})(x^{2} - y^{2}) = x^{4} - y^{4}$
这里我们乘以$-1 × -1$是为了调整顺序,使其与平方差公式的形式相匹配,实际上这一步可以省略,因为$-1 × -1 = 1$,不影响最终结果。
所以,这个多项式是$-x - y$。
【答案】:
D
本题主要考察平方差公式$a^2 - b^2 = (a + b)(a - b)$的应用以及多项式乘法。
首先,我们观察目标表达式$x^{4} - y^{4}$,它可以看作是$(x^{2})^{2} - (y^{2})^{2}$,即平方差的形式。
根据平方差公式,我们可以将其分解为:
$x^{4} - y^{4} = (x^{2} + y^{2})(x^{2} - y^{2})$
接着,我们注意到$x^{2} - y^{2}$还可以继续分解为$(x + y)(x - y)$,所以:
$x^{4} - y^{4} = (x^{2} + y^{2})(x + y)(x - y)$
题目中已经给出了$(-x + y)(y^{2} + x^{2})$,我们需要找到一个多项式,使得它与这个表达式相乘得到$x^{4} - y^{4}$。
对比上述两个表达式,我们可以发现这个多项式应该是$-(x + y)$,即$-x - y$,因为:
$(-x + y)(y^{2} + x^{2})(-x - y) = (x^{2} + y^{2})(x + y)(x - y) × (-1) × (-1) = (x^{2} + y^{2})(x^{2} - y^{2}) = x^{4} - y^{4}$
这里我们乘以$-1 × -1$是为了调整顺序,使其与平方差公式的形式相匹配,实际上这一步可以省略,因为$-1 × -1 = 1$,不影响最终结果。
所以,这个多项式是$-x - y$。
【答案】:
D
3. 如图所示,图中阴影部分的面积等于(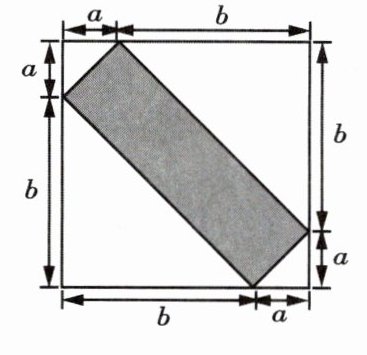
A.$a^{2}+b^{2}$;
B.$a^{2}-b^{2}$;
C.$ab$;
D.$2ab$.
D
)
A.$a^{2}+b^{2}$;
B.$a^{2}-b^{2}$;
C.$ab$;
D.$2ab$.
答案:
D
4. 如果$a^{2}+4= (a - 2)^{2}+m$,那么$m$的值为(
A.$-4a$;
B.$4a$;
C.$2a$;
D.$-2a$.
B
)A.$-4a$;
B.$4a$;
C.$2a$;
D.$-2a$.
答案:
【解析】:
本题考查的是完全平方公式的展开。
首先,我们将等式右边的$(a - 2)^{2}$进行展开,利用完全平方公式$(a-b)^{2}=a^{2}-2ab+b^{2}$,得到$(a - 2)^{2} = a^{2} - 4a + 4$。
然后,将这个结果代入原等式$a^{2} + 4 = (a - 2)^{2} + m$,得到$a^{2} + 4 = a^{2} - 4a + 4 + m$。
接着,我们将等式两边的相同项进行消去,即消去$a^{2}$和$4$,得到$0 = -4a + m$。
最后,我们解这个关于$m$的一元一次方程,得到$m = 4a$。
【答案】:
B
本题考查的是完全平方公式的展开。
首先,我们将等式右边的$(a - 2)^{2}$进行展开,利用完全平方公式$(a-b)^{2}=a^{2}-2ab+b^{2}$,得到$(a - 2)^{2} = a^{2} - 4a + 4$。
然后,将这个结果代入原等式$a^{2} + 4 = (a - 2)^{2} + m$,得到$a^{2} + 4 = a^{2} - 4a + 4 + m$。
接着,我们将等式两边的相同项进行消去,即消去$a^{2}$和$4$,得到$0 = -4a + m$。
最后,我们解这个关于$m$的一元一次方程,得到$m = 4a$。
【答案】:
B
5. 如果$x + y = 1$,$xy= \frac{1}{4}$,那么$x^{2}+y^{2}$的值为(
A.$\frac{1}{4}$;
B.$\frac{1}{2}$;
C.$\frac{3}{2}$;
D.$1$.
B
)A.$\frac{1}{4}$;
B.$\frac{1}{2}$;
C.$\frac{3}{2}$;
D.$1$.
答案:
【解析】:
本题主要考察完全平方公式的应用。
完全平方公式为:$(x+y)^2 = x^2 + 2xy + y^2$。
由此,可以得到$x^2 + y^2 = (x+y)^2 - 2xy$。
根据题目给出的条件,有$x+y=1$和$xy=\frac{1}{4}$。
将这两个条件代入上述公式,可以得到:
$x^2 + y^2 = 1^2 - 2 × \frac{1}{4} = 1 - \frac{1}{2} = \frac{1}{2}$。
【答案】:
B. $\frac{1}{2}$。
本题主要考察完全平方公式的应用。
完全平方公式为:$(x+y)^2 = x^2 + 2xy + y^2$。
由此,可以得到$x^2 + y^2 = (x+y)^2 - 2xy$。
根据题目给出的条件,有$x+y=1$和$xy=\frac{1}{4}$。
将这两个条件代入上述公式,可以得到:
$x^2 + y^2 = 1^2 - 2 × \frac{1}{4} = 1 - \frac{1}{2} = \frac{1}{2}$。
【答案】:
B. $\frac{1}{2}$。
6. 计算:$(a + 2b)(2a - 4b)= $
$2a^{2} - 8b^{2}$
.
答案:
【解析】:
本题主要考查多项式乘多项式的运算,需要应用乘法分配律进行展开。
根据多项式乘法的规则,我们可以将$(a + 2b)$中的每一项分别与$(2a - 4b)$中的每一项相乘,再将得到的积相加。
具体计算过程如下:
$(a + 2b)(2a - 4b)$
$= a × 2a + a × (-4b) + 2b × 2a + 2b × (-4b)$
$= 2a^{2} - 4ab + 4ab - 8b^{2}$
$= 2a^{2} - 8b^{2}$
【答案】:
$2a^{2} - 8b^{2}$
本题主要考查多项式乘多项式的运算,需要应用乘法分配律进行展开。
根据多项式乘法的规则,我们可以将$(a + 2b)$中的每一项分别与$(2a - 4b)$中的每一项相乘,再将得到的积相加。
具体计算过程如下:
$(a + 2b)(2a - 4b)$
$= a × 2a + a × (-4b) + 2b × 2a + 2b × (-4b)$
$= 2a^{2} - 4ab + 4ab - 8b^{2}$
$= 2a^{2} - 8b^{2}$
【答案】:
$2a^{2} - 8b^{2}$
7. 计算:$(\frac{1}{4}a - b)(b + \frac{1}{4}a)= $
$\frac{1}{16}a^{2} - b^{2}$
.
答案:
【解析】:
本题主要考察平方差公式,即$A^2 - B^2 = (A + B)(A - B)$。
在本题中,我们可以将$\frac{1}{4}a$看作$A$,$b$看作$B$,则原式可以转化为平方差公式的形式。
【答案】:
解:原式
$= (\frac{1}{4}a - b)(\frac{1}{4}a + b)$
$= (\frac{1}{4}a)^{2} - b^{2}$
$= \frac{1}{16}a^{2} - b^{2}$
故答案为:$\frac{1}{16}a^{2} - b^{2}$。
本题主要考察平方差公式,即$A^2 - B^2 = (A + B)(A - B)$。
在本题中,我们可以将$\frac{1}{4}a$看作$A$,$b$看作$B$,则原式可以转化为平方差公式的形式。
【答案】:
解:原式
$= (\frac{1}{4}a - b)(\frac{1}{4}a + b)$
$= (\frac{1}{4}a)^{2} - b^{2}$
$= \frac{1}{16}a^{2} - b^{2}$
故答案为:$\frac{1}{16}a^{2} - b^{2}$。
8. 计算:$(a - 3b)(a + b)= $
$a^{2}-2ab-3b^{2}$
.
答案:
【解析】:
本题考查单项式乘多项式的运算,需要应用乘法分配律,即$(a+b)× c=a× c+b× c$。
将$(a - 3b)$中的每一项分别与$(a + b)$中的每一项相乘,然后将得到的积相加,即可得到最终结果。
【答案】:
解:原式
$=a× a+a× b-3b× a-3b× b$
$=a^{2}+ab-3ab-3b^{2}$
$=a^{2}-2ab-3b^{2}$
故答案为:$a^{2}-2ab-3b^{2}$。
本题考查单项式乘多项式的运算,需要应用乘法分配律,即$(a+b)× c=a× c+b× c$。
将$(a - 3b)$中的每一项分别与$(a + b)$中的每一项相乘,然后将得到的积相加,即可得到最终结果。
【答案】:
解:原式
$=a× a+a× b-3b× a-3b× b$
$=a^{2}+ab-3ab-3b^{2}$
$=a^{2}-2ab-3b^{2}$
故答案为:$a^{2}-2ab-3b^{2}$。
9. 计算:$(-\frac{1}{2}a + 1)(-\frac{1}{2}a - 1)= $
$\frac{1}{4}a^{2} - 1$
.
答案:
【解析】:
本题考查平方差公式的运用。题目给出了形式为$(-\frac{1}{2}a + 1)(-\frac{1}{2}a - 1)$,可以观察到它是平方差公式的形式,即$(a+b)(a-b)=a^{2}-b^{2}$。
在本题中,$a = -\frac{1}{2}a$,$b = 1$,所以可以直接利用平方差公式进行计算。
【答案】:
解:原式
$= (-\frac{1}{2}a)^{2} - 1^{2}$
$= \frac{1}{4}a^{2} - 1$
故答案为:$\frac{1}{4}a^{2} - 1$。
本题考查平方差公式的运用。题目给出了形式为$(-\frac{1}{2}a + 1)(-\frac{1}{2}a - 1)$,可以观察到它是平方差公式的形式,即$(a+b)(a-b)=a^{2}-b^{2}$。
在本题中,$a = -\frac{1}{2}a$,$b = 1$,所以可以直接利用平方差公式进行计算。
【答案】:
解:原式
$= (-\frac{1}{2}a)^{2} - 1^{2}$
$= \frac{1}{4}a^{2} - 1$
故答案为:$\frac{1}{4}a^{2} - 1$。
10. 计算:$(2x - 3y)(-3y - 2x)= $
$9y^2 - 4x^2$
.
答案:
【解析】:
本题考查平方差公式的运用。平方差公式为$(a+b)(a-b) = a^2 - b^2$。
在本题中,可以将$(2x - 3y)(-3y - 2x)$视为平方差公式的形式,其中$a = -3y$,$b = 2x$。
根据平方差公式,有:
$(2x - 3y)(-3y - 2x) = (-3y)^2 - (2x)^2$,
进一步展开,得到:
$9y^2 - 4x^2$,
【答案】:
$9y^2 - 4x^2$。
本题考查平方差公式的运用。平方差公式为$(a+b)(a-b) = a^2 - b^2$。
在本题中,可以将$(2x - 3y)(-3y - 2x)$视为平方差公式的形式,其中$a = -3y$,$b = 2x$。
根据平方差公式,有:
$(2x - 3y)(-3y - 2x) = (-3y)^2 - (2x)^2$,
进一步展开,得到:
$9y^2 - 4x^2$,
【答案】:
$9y^2 - 4x^2$。
11. 已知$a + b = 6$,$ab = 10$,则$a^{2}+b^{2}= $
16
.
答案:
【解析】:
本题主要考察代数式的化简与求值,特别是完全平方公式的应用。
已知 $a + b = 6$ 和 $ab = 10$,需要求 $a^{2} + b^{2}$。
根据完全平方公式,有$(a + b)^{2} = a^{2} + 2ab + b^{2}$。
所以$a^{2} + b^{2} = (a + b)^{2} - 2ab$,
将 $a + b = 6$ 和 $ab = 10$ 代入上式,
得$a^{2} + b^{2} = 6^{2} - 2 × 10 = 36 - 20 = 16$。
【答案】:
16
本题主要考察代数式的化简与求值,特别是完全平方公式的应用。
已知 $a + b = 6$ 和 $ab = 10$,需要求 $a^{2} + b^{2}$。
根据完全平方公式,有$(a + b)^{2} = a^{2} + 2ab + b^{2}$。
所以$a^{2} + b^{2} = (a + b)^{2} - 2ab$,
将 $a + b = 6$ 和 $ab = 10$ 代入上式,
得$a^{2} + b^{2} = 6^{2} - 2 × 10 = 36 - 20 = 16$。
【答案】:
16
12. 若一个正方形的边长增加$2$厘米,面积就增加$12$平方厘米,则这个正方形的边长是
2厘米
.
答案:
【解析】:
本题主要考查正方形的面积公式以及一元一次方程的建立和求解。
设原正方形的边长为$x$厘米,则原正方形的面积为$x^2$平方厘米。
根据题意,正方形的边长增加2厘米后,新的边长为$x+2$厘米,新的面积为$(x+2)^2$平方厘米。
由题意知,新的面积比原面积多12平方厘米,所以有方程:
$(x+2)^2 - x^2 = 12$
展开并整理得:
$x^2 + 4x + 4 - x^2 = 12$
$4x = 8$
$x = 2$
所以,原正方形的边长为2厘米。
【答案】:
2厘米。
本题主要考查正方形的面积公式以及一元一次方程的建立和求解。
设原正方形的边长为$x$厘米,则原正方形的面积为$x^2$平方厘米。
根据题意,正方形的边长增加2厘米后,新的边长为$x+2$厘米,新的面积为$(x+2)^2$平方厘米。
由题意知,新的面积比原面积多12平方厘米,所以有方程:
$(x+2)^2 - x^2 = 12$
展开并整理得:
$x^2 + 4x + 4 - x^2 = 12$
$4x = 8$
$x = 2$
所以,原正方形的边长为2厘米。
【答案】:
2厘米。
13. 正方形的边长是$a$厘米,若将一边增加$3$厘米,另一边减少$3$厘米,则新图形的面积比原正方形的面积
少
9
平方厘米.
答案:
【解析】:
本题主要考察平方差公式的应用以及代数式的运算。
首先,我们需要计算原正方形的面积,根据正方形面积的计算公式,面积 $S = a^2$,其中 $a$ 是正方形的边长。
然后,我们需要计算新图形的面积。
根据题目,新图形的一边长是 $a + 3$ 厘米,另一边长是 $a - 3$ 厘米。
因此,新图形的面积 $S' = (a + 3)(a - 3)$。
接下来,我们需要比较新图形的面积和原正方形的面积,即计算 $S' - S$。
利用平方差公式,我们可以将 $S'$ 展开为 $a^2 - 9$。
因此,$S' - S = (a^2 - 9) - a^2 = -9$。
由于 $S' - S = -9 \lt 0$,所以新图形的面积比原正方形的面积少 9 平方厘米。
【答案】:
少;9
本题主要考察平方差公式的应用以及代数式的运算。
首先,我们需要计算原正方形的面积,根据正方形面积的计算公式,面积 $S = a^2$,其中 $a$ 是正方形的边长。
然后,我们需要计算新图形的面积。
根据题目,新图形的一边长是 $a + 3$ 厘米,另一边长是 $a - 3$ 厘米。
因此,新图形的面积 $S' = (a + 3)(a - 3)$。
接下来,我们需要比较新图形的面积和原正方形的面积,即计算 $S' - S$。
利用平方差公式,我们可以将 $S'$ 展开为 $a^2 - 9$。
因此,$S' - S = (a^2 - 9) - a^2 = -9$。
由于 $S' - S = -9 \lt 0$,所以新图形的面积比原正方形的面积少 9 平方厘米。
【答案】:
少;9
14. 计算:$99×101= ($
100 - 1
$)×($100 + 1
$)= $9999
.
答案:
【解析】:
题目考查了平方差公式的应用,即$a^2 - b^2 = (a+b)(a-b)$。
在本题中,可以将$99$和$101$分别看作$(100-1)$和$(100+1)$,
然后利用平方差公式进行计算。
【答案】:
原式$ = (100 - 1)×(100 + 1)$
$= 100^2 - 1^2$
$= 10000 - 1$
$= 9999$。
题目考查了平方差公式的应用,即$a^2 - b^2 = (a+b)(a-b)$。
在本题中,可以将$99$和$101$分别看作$(100-1)$和$(100+1)$,
然后利用平方差公式进行计算。
【答案】:
原式$ = (100 - 1)×(100 + 1)$
$= 100^2 - 1^2$
$= 10000 - 1$
$= 9999$。
15. (1)如图1,阴影部分的面积是
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是
(3)比较上面两个图阴影部分的面积,可以得到乘法公式:
$a^2 - b^2$
(写成两数平方差的形式);(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是
$a - b$
,长是$a + b$
,面积是$(a + b)(a - b)$
(写成多项式乘法的形式);(3)比较上面两个图阴影部分的面积,可以得到乘法公式:
$(a + b)(a - b) = a^2 - b^2$
.
答案:
(1) $a^2 - b^2$
(2) $a - b$;$a + b$;$(a + b)(a - b)$
(3) $(a + b)(a - b) = a^2 - b^2$
(1) $a^2 - b^2$
(2) $a - b$;$a + b$;$(a + b)(a - b)$
(3) $(a + b)(a - b) = a^2 - b^2$
查看更多完整答案,请扫码查看


