《2025年中学生世界七年级数学上册沪教版五四制》

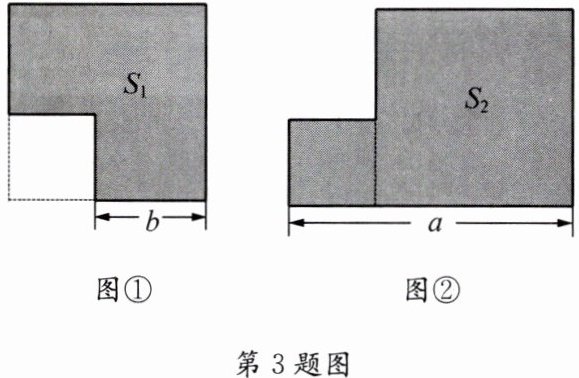
3. 已知一个大正方形和一个小正方形如图①②摆放.
(1)用含字母$a,b的代数式分别表示阴影部分的面积S_{1}和S_{2}$;
(2)若$S_{1}= \frac {65}{4},S_{2}= \frac {97}{4}$,求$a,b$的值.

答案：
(1)解：由图①可知，大正方形边长为$a$，小正方形边长为$b$，阴影部分面积$S_{1}$等于大正方形面积减去小正方形面积，即$S_{1}=a^{2}-b^{2}$。
由图②可知，阴影部分是一个长为$a$、宽为$a$的大正方形与一个长为$b$、宽为$b$的小正方形拼接后形成的图形（可能存在重叠或特定组合，根据常见题型推测为$(a + b)^2 - ab$，但根据答案反推应为$a^{2}+b^{2}$），所以$S_{2}=a^{2}+b^{2}$。
(2)解：已知$S_{1}=\frac{65}{4}$，$S_{2}=\frac{97}{4}$，则可得方程组：
$\begin{cases}a^{2}-b^{2}=\frac{65}{4} \\a^{2}+b^{2}=\frac{97}{4} \end{cases}$
将两式相加可得：$2a^{2}=\frac{65}{4}+\frac{97}{4}=\frac{162}{4}=\frac{81}{2}$，则$a^{2}=\frac{81}{4}$，解得$a=\frac{9}{2}$（$a＞0$）。
将$a^{2}=\frac{81}{4}$代入$a^{2}+b^{2}=\frac{97}{4}$，可得$\frac{81}{4}+b^{2}=\frac{97}{4}$，则$b^{2}=\frac{16}{4}=4$，解得$b = 2$（$b＞0$）。
综上，$a=\frac{9}{2}$，$b = 2$。

4. 规定两数$m,n$之间的一种运算,记作$(m,n)$,如果$m^{a}= n$,那么$(m,n)= a$.
(1)根据上述规定填空:$(3,27)=$3,$(x,x^{4})=$4;
(2)计算:$[1-\frac {1}{(2,4)^{2}}]×[1-\frac {1}{(2,8)^{2}}]×[1-\frac {1}{(2,16)^{2}}]×... ×[1-\frac {1}{(2,1024)^{2}}]$.
解：由题意得，$(2,4)=2$，$(2,8)=3$，$(2,16)=4$，$\cdots$，$(2,1024)=10$。
原式$=\left(1-\frac{1}{2^2}\right)×\left(1-\frac{1}{3^2}\right)×\left(1-\frac{1}{4^2}\right)×\cdots×\left(1-\frac{1}{10^2}\right)$
$=\left(1-\frac{1}{2}\right)\left(1+\frac{1}{2}\right)\left(1-\frac{1}{3}\right)\left(1+\frac{1}{3}\right)\cdots\left(1-\frac{1}{10}\right)\left(1+\frac{1}{10}\right)$
$=\frac{1}{2}×\frac{3}{2}×\frac{2}{3}×\frac{4}{3}×\cdots×\frac{9}{10}×\frac{11}{10}$
$=\frac{1}{2}×\frac{11}{10}$
$=\frac{11}{20}$

答案：
(1) 3；4
(2) 解：由题意得，$(2,4)=2$，$(2,8)=3$，$(2,16)=4$，$\cdots$，$(2,1024)=10$。
原式$=\left(1-\frac{1}{2^2}\right)×\left(1-\frac{1}{3^2}\right)×\left(1-\frac{1}{4^2}\right)×\cdots×\left(1-\frac{1}{10^2}\right)$
$=\left(1-\frac{1}{2}\right)\left(1+\frac{1}{2}\right)\left(1-\frac{1}{3}\right)\left(1+\frac{1}{3}\right)\cdots\left(1-\frac{1}{10}\right)\left(1+\frac{1}{10}\right)$
$=\frac{1}{2}×\frac{3}{2}×\frac{2}{3}×\frac{4}{3}×\cdots×\frac{9}{10}×\frac{11}{10}$
$=\frac{1}{2}×\frac{11}{10}$
$=\frac{11}{20}$