16. 计算:
(1)$(4a - b) \cdot (-2b)^{2}$;(2)$(\frac{3}{2}x^{2}+xy-\frac{3}{5}y^{2}) \cdot (-\frac{4}{3}x^{2}y)$.
(1)$(4a - b) \cdot (-2b)^{2}$;(2)$(\frac{3}{2}x^{2}+xy-\frac{3}{5}y^{2}) \cdot (-\frac{4}{3}x^{2}y)$.
答案:
(1)解:原式=(4a - b)·4b²
=4a·4b² - b·4b²
=16ab² - 4b³
(2)解:原式=$\frac{3}{2}x^{2}·(-\frac{4}{3}x^{2}y)+xy·(-\frac{4}{3}x^{2}y)-\frac{3}{5}y^{2}·(-\frac{4}{3}x^{2}y)$
=$-2x^{4}y - \frac{4}{3}x^{3}y^{2} + \frac{4}{5}x^{2}y^{3}$
(1)解:原式=(4a - b)·4b²
=4a·4b² - b·4b²
=16ab² - 4b³
(2)解:原式=$\frac{3}{2}x^{2}·(-\frac{4}{3}x^{2}y)+xy·(-\frac{4}{3}x^{2}y)-\frac{3}{5}y^{2}·(-\frac{4}{3}x^{2}y)$
=$-2x^{4}y - \frac{4}{3}x^{3}y^{2} + \frac{4}{5}x^{2}y^{3}$
17. 解方程:$x(3 - 2x + x^{2})= x^{2}(x - 2)+5(x - 1)$.
答案:
解:$x(3 - 2x + x^{2})= x^{2}(x - 2)+5(x - 1)$
$3x - 2x^{2} + x^{3} = x^{3} - 2x^{2} + 5x - 5$
$3x - 2x^{2} + x^{3} - x^{3} + 2x^{2} - 5x = -5$
$-2x = -5$
$x = \frac{5}{2}$
$3x - 2x^{2} + x^{3} = x^{3} - 2x^{2} + 5x - 5$
$3x - 2x^{2} + x^{3} - x^{3} + 2x^{2} - 5x = -5$
$-2x = -5$
$x = \frac{5}{2}$
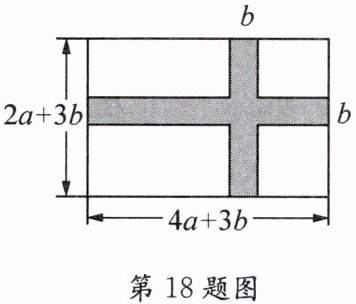
18. 如图,为了提高宜居环境,某小区准备在一个长为$(4a + 3b)$米,宽为$(2a + 3b)米的长方形草坪上修建两条宽为b$米的通道.求:
(1)通道的面积是多少平方米?
(2)剩余草坪的面积是多少平方米?
(1)通道的面积是多少平方米?
(2)剩余草坪的面积是多少平方米?

答案:
【解析】:本题主要考查整式的乘法运算以及面积的计算。
(1)对于通道面积的计算,需要分别计算横向和纵向通道的面积,然后相加,同时要减去它们重叠的部分。
横向通道的长为$(4a + 3b)$米,宽为$b$米,根据长方形面积公式$S = 长×宽$,其面积为$(4a + 3b)× b=4ab + 3b^{2}$平方米。
纵向通道的长为$(2a + 3b)$米,宽为$b$米,其面积为$(2a + 3b)× b = 2ab+3b^{2}$平方米。
而它们重叠的部分是一个边长为$b$米的正方形,面积为$b× b = b^{2}$平方米。
所以通道的面积为横向通道面积与纵向通道面积之和减去重叠部分的面积,即$(4ab + 3b^{2})+(2ab + 3b^{2})-b^{2}=4ab + 3b^{2}+2ab + 3b^{2}-b^{2}=6ab + 5b^{2}$平方米。
(2)对于剩余草坪面积的计算,先根据长方形面积公式求出整个长方形草坪的面积,再用草坪面积减去通道面积。
整个长方形草坪的长为$(4a + 3b)$米,宽为$(2a + 3b)$米,所以其面积为$(4a + 3b)×(2a + 3b)$平方米。
根据多项式乘法法则展开$(4a + 3b)×(2a + 3b)=4a×(2a + 3b)+3b×(2a + 3b)=8a^{2}+12ab + 6ab+9b^{2}=8a^{2}+18ab + 9b^{2}$平方米。
由(1)已求得通道面积为$(6ab + 5b^{2})$平方米,所以剩余草坪面积为$(8a^{2}+18ab + 9b^{2})-(6ab + 5b^{2})=8a^{2}+18ab + 9b^{2}-6ab - 5b^{2}=8a^{2}+12ab + 4b^{2}$平方米。
【答案】:
(1)$(6ab + 5b^{2})$平方米;
(2)$(8a^{2}+12ab + 4b^{2})$平方米
(1)对于通道面积的计算,需要分别计算横向和纵向通道的面积,然后相加,同时要减去它们重叠的部分。
横向通道的长为$(4a + 3b)$米,宽为$b$米,根据长方形面积公式$S = 长×宽$,其面积为$(4a + 3b)× b=4ab + 3b^{2}$平方米。
纵向通道的长为$(2a + 3b)$米,宽为$b$米,其面积为$(2a + 3b)× b = 2ab+3b^{2}$平方米。
而它们重叠的部分是一个边长为$b$米的正方形,面积为$b× b = b^{2}$平方米。
所以通道的面积为横向通道面积与纵向通道面积之和减去重叠部分的面积,即$(4ab + 3b^{2})+(2ab + 3b^{2})-b^{2}=4ab + 3b^{2}+2ab + 3b^{2}-b^{2}=6ab + 5b^{2}$平方米。
(2)对于剩余草坪面积的计算,先根据长方形面积公式求出整个长方形草坪的面积,再用草坪面积减去通道面积。
整个长方形草坪的长为$(4a + 3b)$米,宽为$(2a + 3b)$米,所以其面积为$(4a + 3b)×(2a + 3b)$平方米。
根据多项式乘法法则展开$(4a + 3b)×(2a + 3b)=4a×(2a + 3b)+3b×(2a + 3b)=8a^{2}+12ab + 6ab+9b^{2}=8a^{2}+18ab + 9b^{2}$平方米。
由(1)已求得通道面积为$(6ab + 5b^{2})$平方米,所以剩余草坪面积为$(8a^{2}+18ab + 9b^{2})-(6ab + 5b^{2})=8a^{2}+18ab + 9b^{2}-6ab - 5b^{2}=8a^{2}+12ab + 4b^{2}$平方米。
【答案】:
(1)$(6ab + 5b^{2})$平方米;
(2)$(8a^{2}+12ab + 4b^{2})$平方米
1. $a(m - n)^{p} \cdot (n - m)^{q} \cdot (m - n)^{q} \cdot (n - m)^{p}= $
$a(m - n)^{2(p + q)}$
.
答案:
【解析】:
本题主要考察整式的乘法以及同底数幂的乘法法则。
首先,我们注意到$(m - n)$和$(n - m)$是互为相反数的,即$(m - n) = -(n - m)$。
原式可以写为:
$a(m - n)^{p} \cdot (n - m)^{q} \cdot (m - n)^{q} \cdot (n - m)^{p}$
$= a(m - n)^{p} \cdot (-1)^{q}(m - n)^{q} \cdot (m - n)^{q} \cdot (-1)^{p}(m - n)^{p}$
根据同底数幂的乘法法则,即$a^m × a^n = a^{m+n}$,我们可以将上式进一步化简为:
$= a(-1)^{p+q}(m - n)^{p+q+q+p}$
$= a(-1)^{p+q}(m - n)^{2p+2q}$
但是,由于$(m - n)$和$(n - m)$的符号差异,我们需要考虑$p+q$的奇偶性:
当$p+q$为偶数时,$(-1)^{p+q} = 1$,所以原式$= a(m - n)^{2(p+q)}$;
当$p+q$为奇数时,$(-1)^{p+q} = -1$,但由于我们只关心$(m-n)$的幂次和符号(因为a是系数,不影响$(m-n)$的幂次和符号),
而两个$(m-n)$的幂相乘,其结果的符号总是正的,所以最终原式的符号由a和$(-1)^{p+q}$的乘积决定,但在此我们只考虑$(m-n)$的幂次,
因此可以统一写为原式$= a(n - m)^{2(p+q)}$(注意这里我们选择了$(n-m)$作为底数,但结果与$(m-n)$作为底数时相同,因为两者只是符号相反,而幂次是偶数)。
但更简洁且符合题目意图的写法是忽略$(-1)^{p+q}$的符号(因为题目只问了$(m-n)$或$(n-m)$的幂次形式),所以直接写为:
$= a(m - n)^{2(p+q)}$(或等价地$= a(n - m)^{2(p+q)}$)
但通常我们选择一种形式作为标准答案,这里选择$(m-n)$作为底数。
【答案】:
$a(m - n)^{2(p + q)}$
本题主要考察整式的乘法以及同底数幂的乘法法则。
首先,我们注意到$(m - n)$和$(n - m)$是互为相反数的,即$(m - n) = -(n - m)$。
原式可以写为:
$a(m - n)^{p} \cdot (n - m)^{q} \cdot (m - n)^{q} \cdot (n - m)^{p}$
$= a(m - n)^{p} \cdot (-1)^{q}(m - n)^{q} \cdot (m - n)^{q} \cdot (-1)^{p}(m - n)^{p}$
根据同底数幂的乘法法则,即$a^m × a^n = a^{m+n}$,我们可以将上式进一步化简为:
$= a(-1)^{p+q}(m - n)^{p+q+q+p}$
$= a(-1)^{p+q}(m - n)^{2p+2q}$
但是,由于$(m - n)$和$(n - m)$的符号差异,我们需要考虑$p+q$的奇偶性:
当$p+q$为偶数时,$(-1)^{p+q} = 1$,所以原式$= a(m - n)^{2(p+q)}$;
当$p+q$为奇数时,$(-1)^{p+q} = -1$,但由于我们只关心$(m-n)$的幂次和符号(因为a是系数,不影响$(m-n)$的幂次和符号),
而两个$(m-n)$的幂相乘,其结果的符号总是正的,所以最终原式的符号由a和$(-1)^{p+q}$的乘积决定,但在此我们只考虑$(m-n)$的幂次,
因此可以统一写为原式$= a(n - m)^{2(p+q)}$(注意这里我们选择了$(n-m)$作为底数,但结果与$(m-n)$作为底数时相同,因为两者只是符号相反,而幂次是偶数)。
但更简洁且符合题目意图的写法是忽略$(-1)^{p+q}$的符号(因为题目只问了$(m-n)$或$(n-m)$的幂次形式),所以直接写为:
$= a(m - n)^{2(p+q)}$(或等价地$= a(n - m)^{2(p+q)}$)
但通常我们选择一种形式作为标准答案,这里选择$(m-n)$作为底数。
【答案】:
$a(m - n)^{2(p + q)}$
2. 若$(x^{2}+x - 2) \cdot (x^{2}-x - 2)^{3}= a_{8}x^{8}+a_{7}x^{7}+… +a_{2}x^{2}+a_{1}x + a_{0}$,试求$a_{0}+a_{1}+… +a_{7}+a_{8}$的值.
答案:
解:令$x = 1$,则
左边$=(1^{2} + 1 - 2) \cdot (1^{2} - 1 - 2)^{3}$
$=(1 + 1 - 2) \cdot (1 - 1 - 2)^{3}$
$=0 \cdot (-2)^{3}$
$=0$
右边$=a_{8} \cdot 1^{8} + a_{7} \cdot 1^{7} + \cdots + a_{1} \cdot 1 + a_{0} = a_{8} + a_{7} + \cdots + a_{1} + a_{0}$
所以$a_{0} + a_{1} + \cdots + a_{7} + a_{8} = 0$
答案:$0$
左边$=(1^{2} + 1 - 2) \cdot (1^{2} - 1 - 2)^{3}$
$=(1 + 1 - 2) \cdot (1 - 1 - 2)^{3}$
$=0 \cdot (-2)^{3}$
$=0$
右边$=a_{8} \cdot 1^{8} + a_{7} \cdot 1^{7} + \cdots + a_{1} \cdot 1 + a_{0} = a_{8} + a_{7} + \cdots + a_{1} + a_{0}$
所以$a_{0} + a_{1} + \cdots + a_{7} + a_{8} = 0$
答案:$0$
查看更多完整答案,请扫码查看


